2.5.2 Пересекающиеся прямые

2.5.2.1 Модель ортогонального проецирования пересекающихся прямых (рис.23)

Если прямые пересекаются, то они имеют общую точку. Одноименные проекции пересекающихся прямых пересекаются в точке, которая является проекцией их общей точки.

Пересекаются пары прямых – (AD ∩ CB) и (ST ∩ LK). Прямые AD и CB пересекаются в точке R, следовательно их проекции A⁰D⁰ и C⁰ B⁰ пересекаются в точке R⁰, которая является проекцией точки R на плоскость проекций π₀. Прямые ST и LK пересекаются в точке Q, следовательно их проекции S⁰T ⁰ и L⁰ K⁰ пересекаются в точке Q⁰, которая является проекцией точки Q на

плоскость проекций π₀ . Так как прямые т ST и LK лежат в плоскости, перпендикулярной плоскости проекций π₀, то их проекции

совпадают (S⁰ T⁰≡ L⁰ K⁰).

Р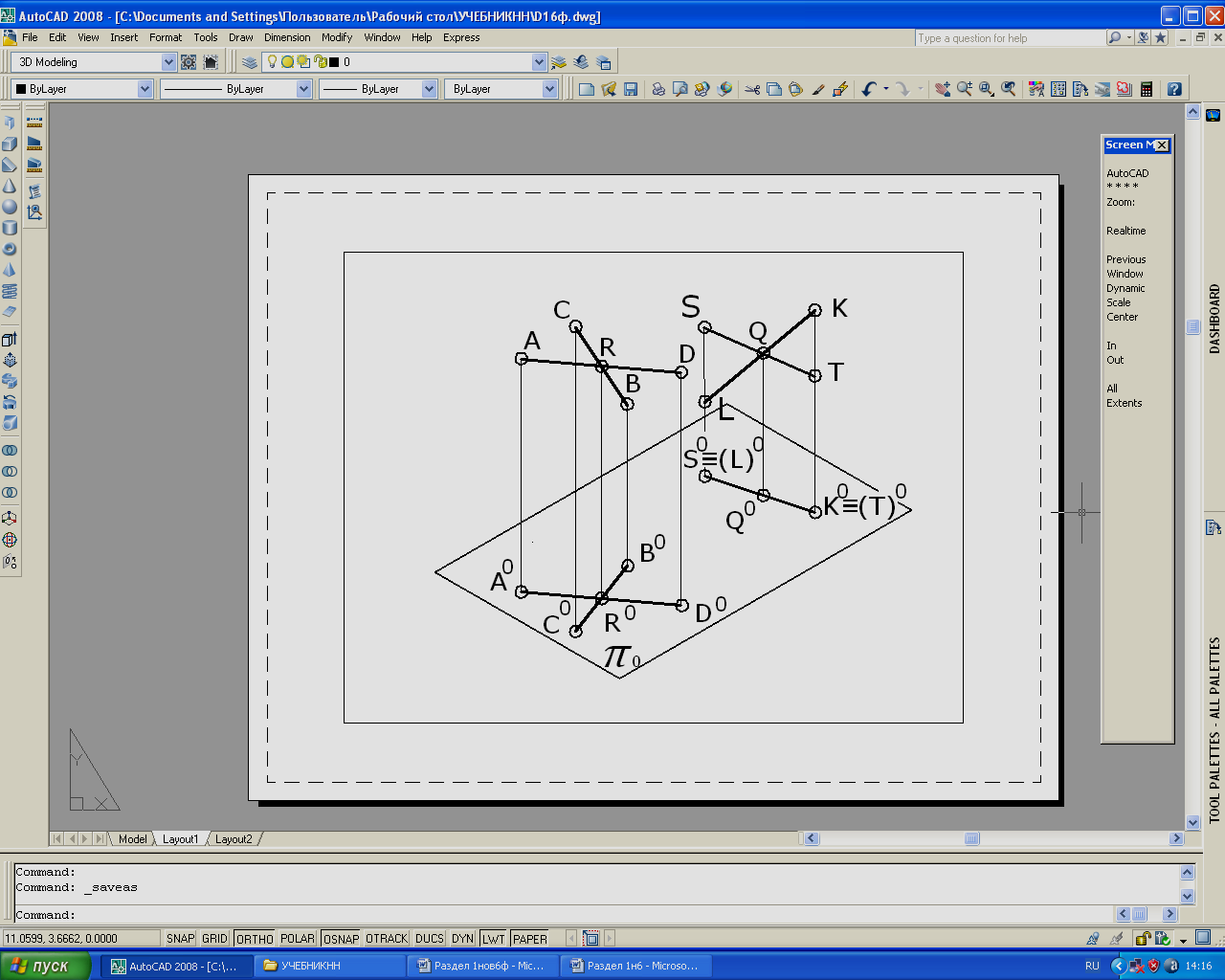ис. 23. Модель ортогонального проецирования

пересекающихся прямых.

2.5.2.2 Чертежи ортогонального проецирования параллельных прямых (рис.24)

а) (AB ∩ CD), (MN ∩ LK); б) (EF ∩ PR).

Прямые AB и CD пересекаются в точке V, следовательно их проекции: (A’ B’ ∩ C’ D’ = V’) , (A’’ B’’ ∩ C’’D’’ = V’’) пересекаются в точках V’ и V’’ и эти точки лежат на одной линии связи, перпендикулярной оси проекций «XO».

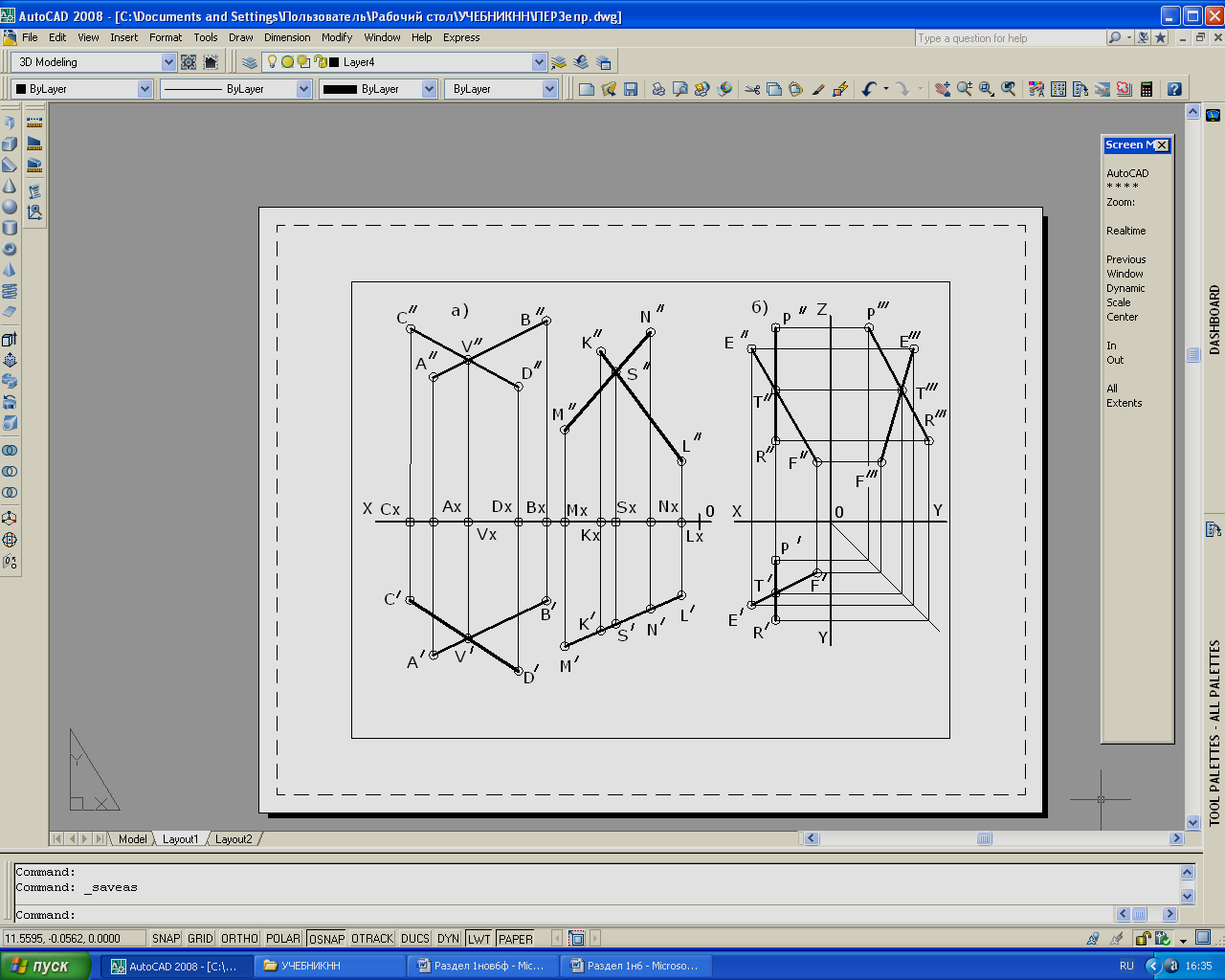
Рис. 24. Пересекающиеся прямые.

а) Проекции прямых на две плоскости проекций (π₁ и π₂).

б) Проекции прямых на три плоскости проекций (π₁ , π₂ и π₃).

Пересекаются пары прямых:

Прямые MN и LK пересекаются в точке S, следовательно их проекции: (M’ N’ ∩ L’ K’ = S’) , (M’’ N’’ ∩ L’’K’’ = S’’) пересекаются в точках S’ и S’’и эти точки лежат на одной линии связи, перпендикулярной оси проекций «XO».

Прямые EF и PR пересекаются в точке T, следовательно их проекции: (E’F’ ∩ P’R’ = T’), (E’’ F’’ ∩ P’’R’’ = T’’) и (E’’’F’’’ ∩ P’’’ R’’’ = T’’’) пересекаются в точках T’ , T’’ и T’’’. Эти точки попарно лежат на линиях связи, перпендикулярных осям проекций: «XO», «YO» и «ZO» соответственно.

Из сказанного следует:

1. Если прямые пересекаются, то их одноименные проекции пересекаются, а точки пересечения проекций лежат на одной линии связи.

2. Если пересекающиеся прямые лежат в плоскости перпендикулярной плоскости проекций, то их проекции на эту плоскость совпадают (рис.25).

2.5.3 Скрещивающиеся прямые

Скрещивающиеся прямые линии не пересекаются и не параллельны между собой.

2.5.3.1 Модель ортогонального проецирования скрещивающихся прямых (рис.25)

Прямые AD и CB (рис.25) не являются параллельными и не пересекаются между собой. Их проекции могут пересекаться

(A⁰D⁰∩C⁰B⁰=[E⁰≡J⁰]), но в точку пересечения проекций проецируются две разные точки (E и J), принадлежащие разным прямым (E принадлежит прямой CB, J принадлежит прямой AD).

Проекции скрещивающихся прямых LQ и SK параллельны (L⁰Q⁰ // S⁰K⁰), так как прямые лежат в параллельных проецирующих плоскостях.

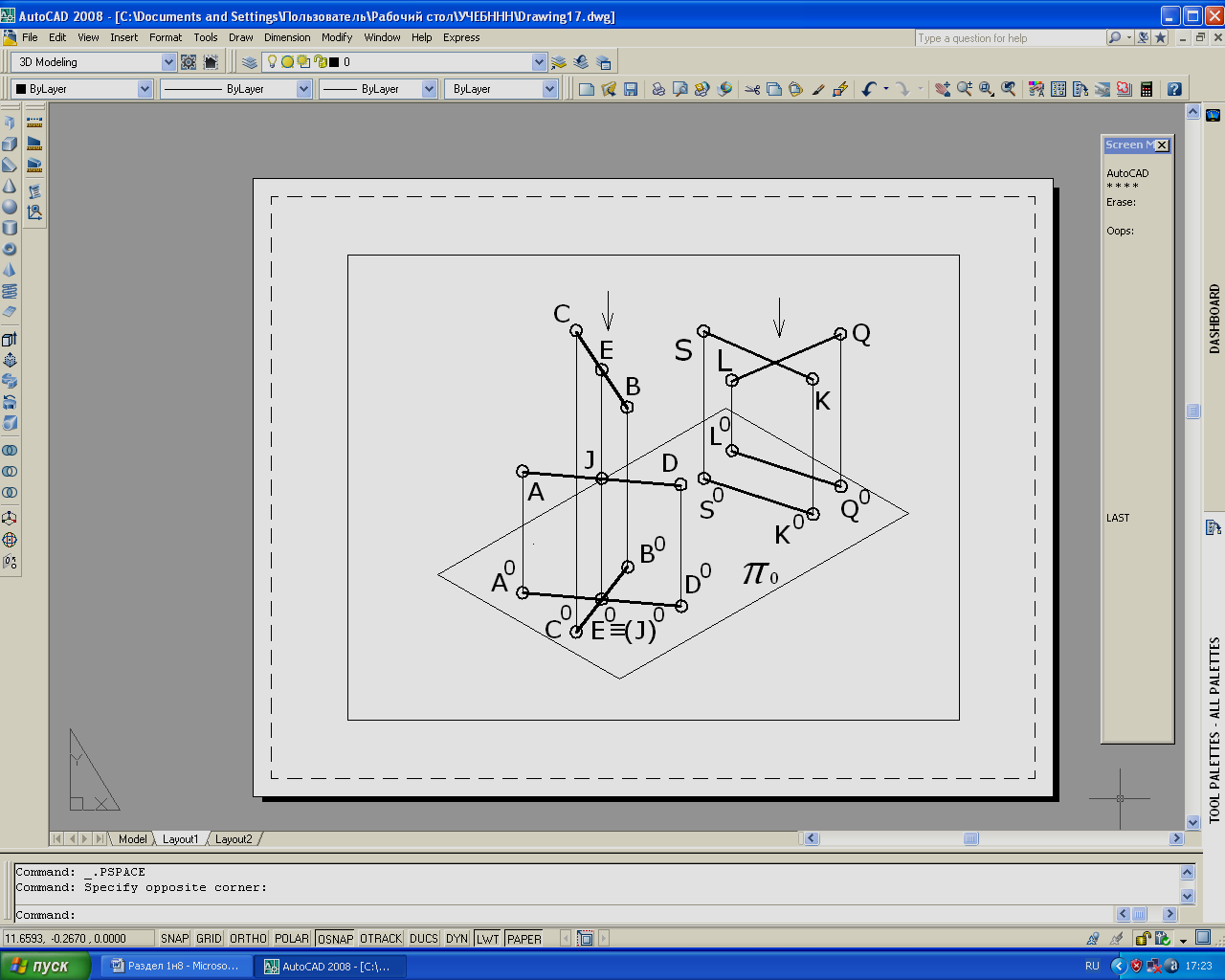
Рис. 25. Модель ортогонального проецирования

скрещивающихся прямых.