
- •Лабораторне заняття 2 Тема: Основні алгебраїчні структури
- •1. Бінарні алгебраїчні операції
- •Властивості бінарних алгебраїчних операцій
- •2. Групи
- •3. Кільця
- •4. Поля
- •5. Ізоморфізми та гомоморфізми алгебраїчних структур
- •6. Векторні простори. Алгебри
- •Означення. Лінійною комбінацією векторів векторного простору називається вектор вигляду
- •1. Бінарні алгебраїчні операції
- •2. Групи
- •Групи підстановок
- •4. Кільця і поля
- •5. Ізоморфізми та гомоморфізми алгебраїчних структур
- •6. Векторні простори. Алгебри
5. Ізоморфізми та гомоморфізми алгебраїчних структур
Завдання 5.
-
Довести, що експоненціальна функція
 є гомоморфізмом (і навіть ізоморфізмом)
адитивної групи
є гомоморфізмом (і навіть ізоморфізмом)
адитивної групи
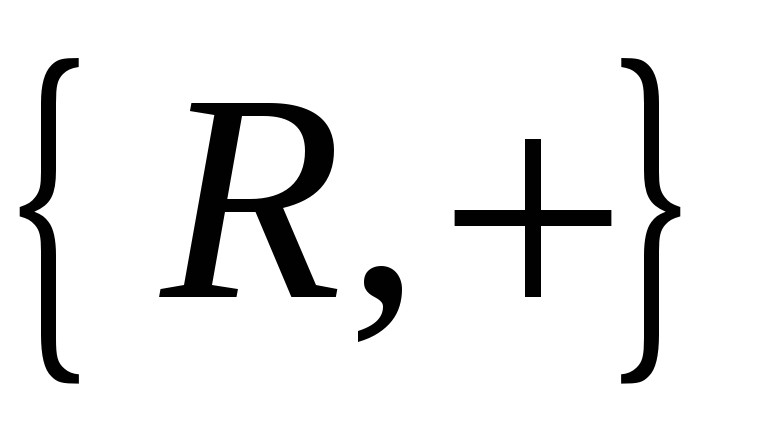 в мультиплікативну групу
в мультиплікативну групу
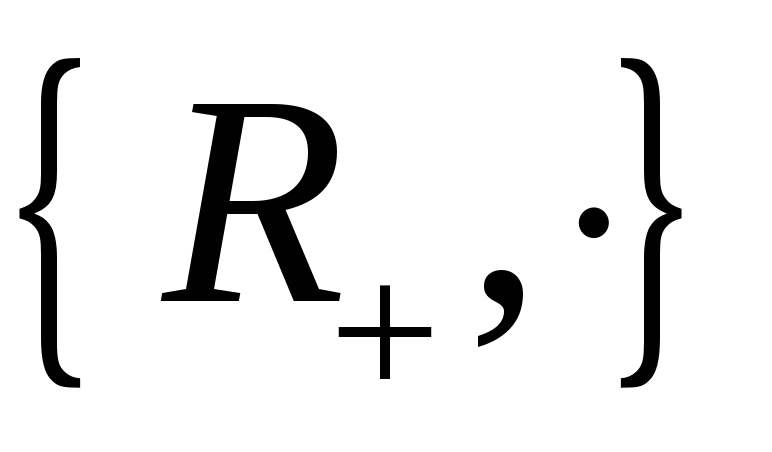 .
. -
Довести, що
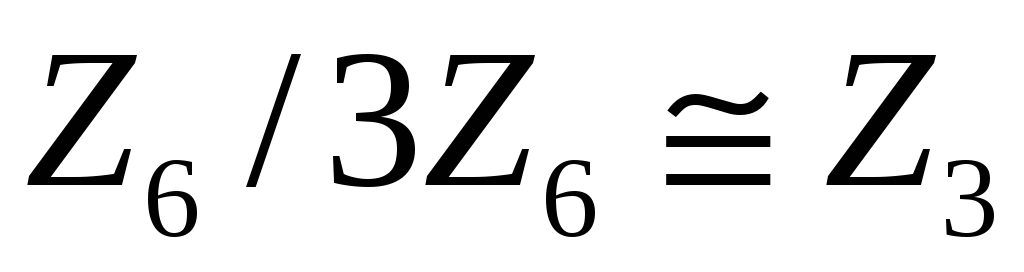 .
. -
Довести, що кільце
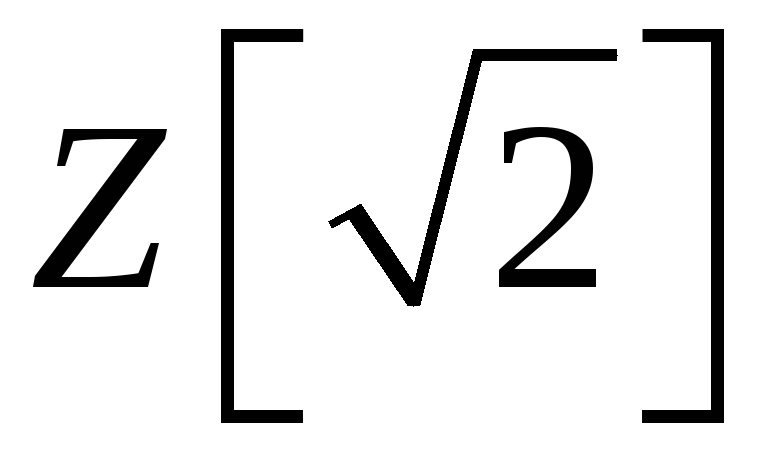 чисел вигляду
чисел вигляду
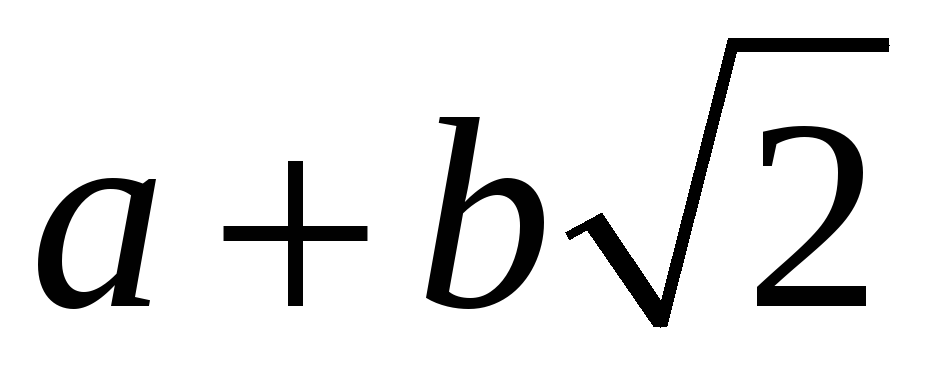 ,
де
,
де
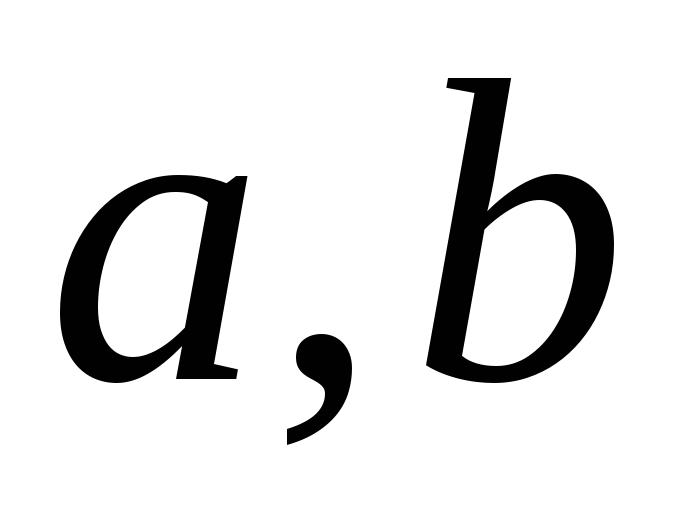 – цілі числа, ізоморфне кільцю матриць
вигляду
– цілі числа, ізоморфне кільцю матриць
вигляду
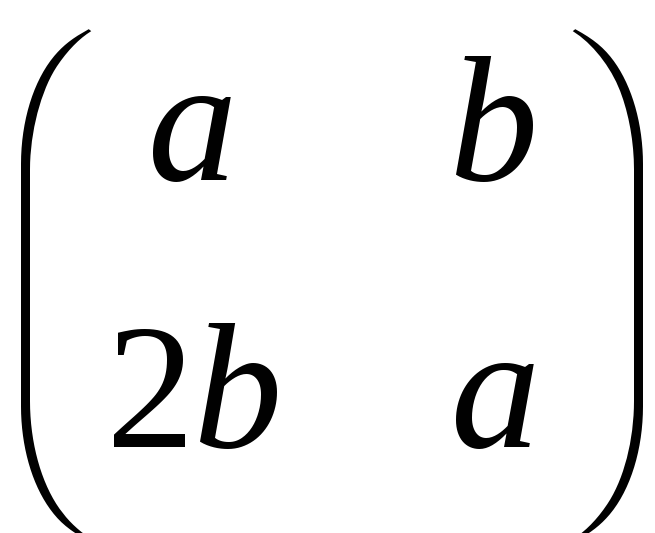 ,
,
 .
. -
Довести, що відображення
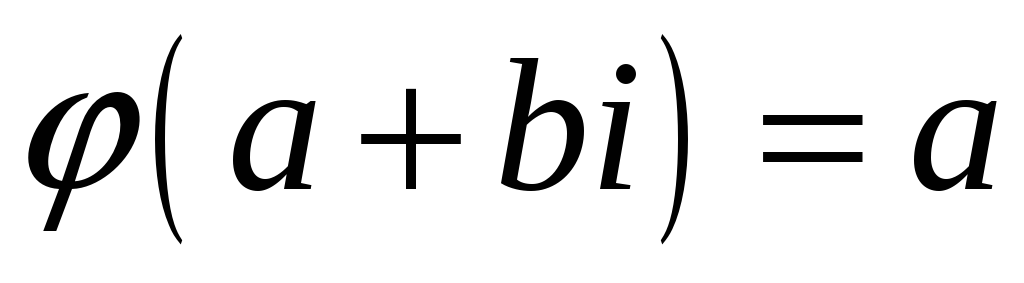 є гомоморфізмом адитивної групи
комплексних чисел на адитивну групу
дійсних чисел.
є гомоморфізмом адитивної групи
комплексних чисел на адитивну групу
дійсних чисел. -
Довести, що поле матриць
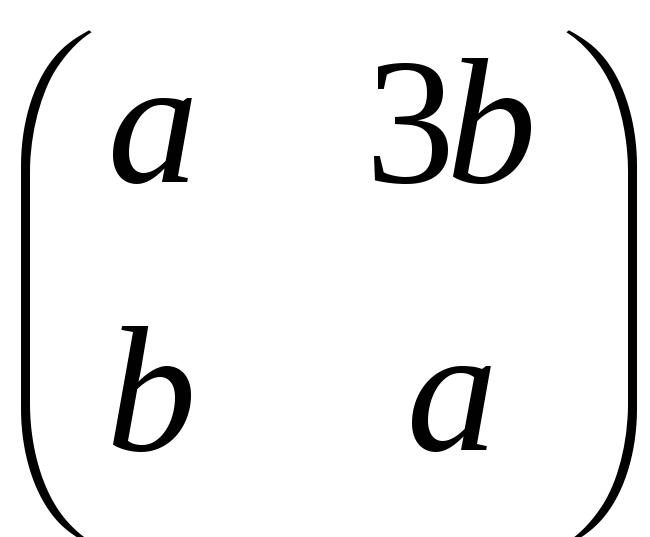 ,
де
,
де
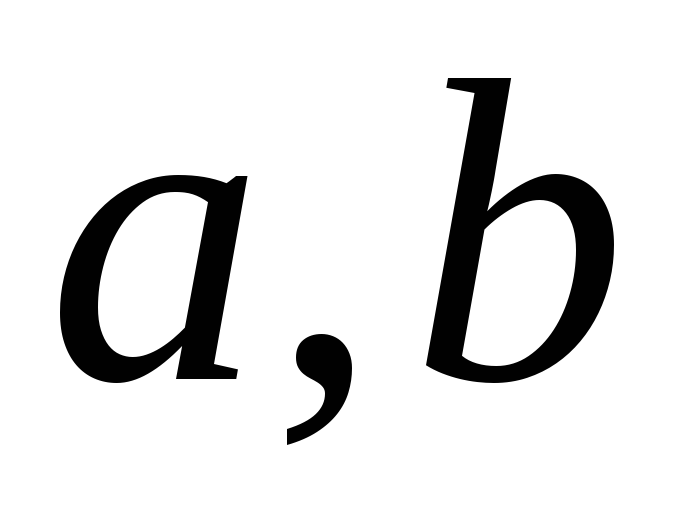 – раціональні числа,
ізоморфне полю
– раціональні числа,
ізоморфне полю
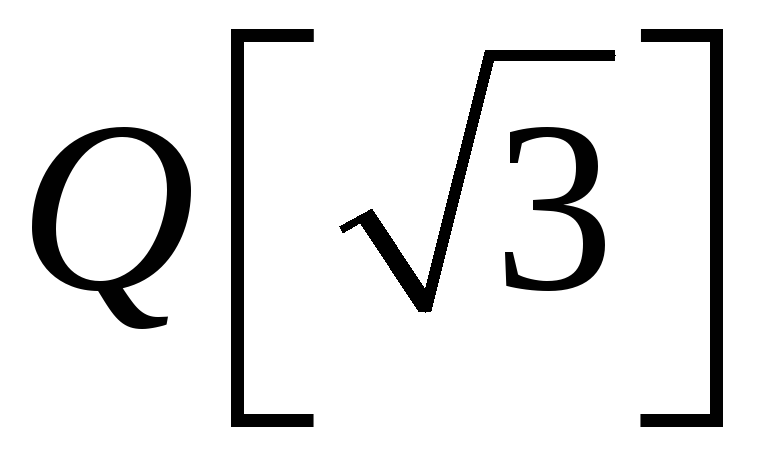 чисел вигляду
чисел вигляду
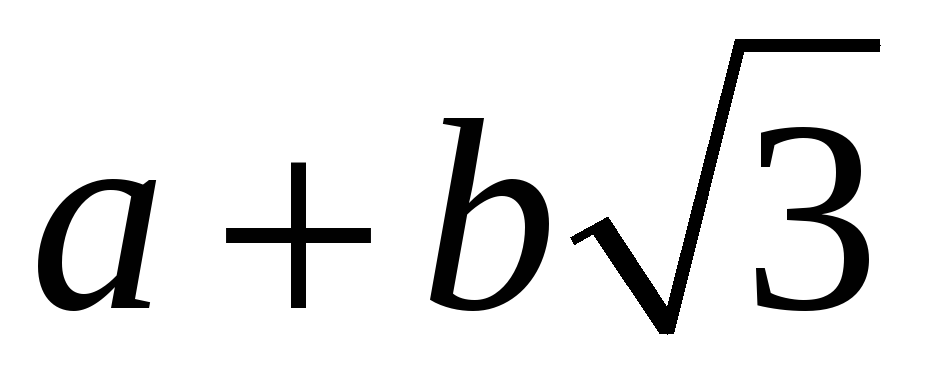 ,
де
,
де
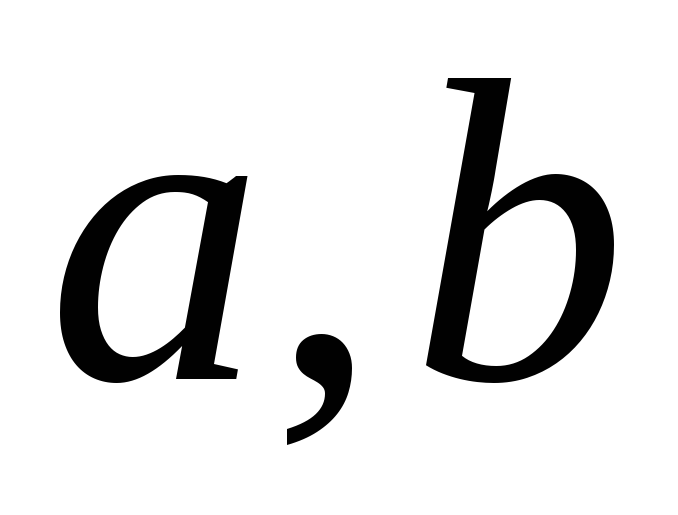 – раціональні числа
– раціональні числа -
Довести, що
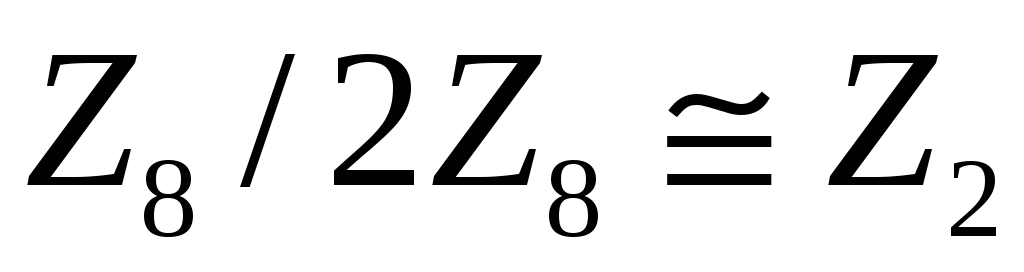 .
. -
Довести, що множина матриць
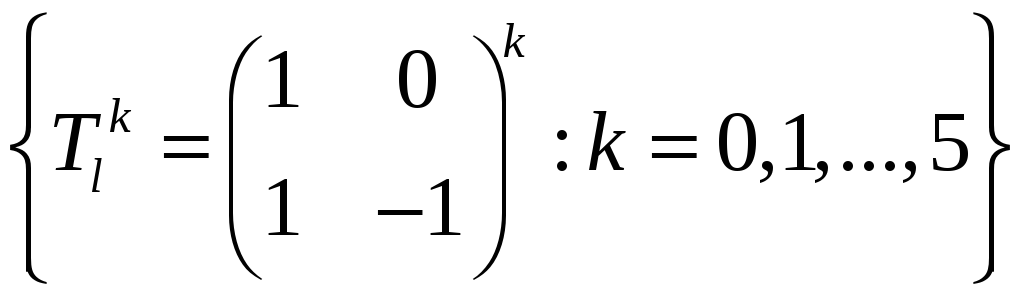 є групою відносно операції множення
матриць, ізоморфною циклічній групі
6-го порядку.
є групою відносно операції множення
матриць, ізоморфною циклічній групі
6-го порядку. -
Довести, що
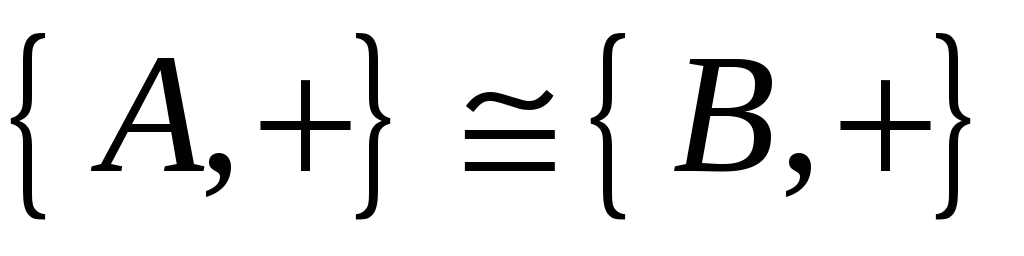 ,
де
,
де
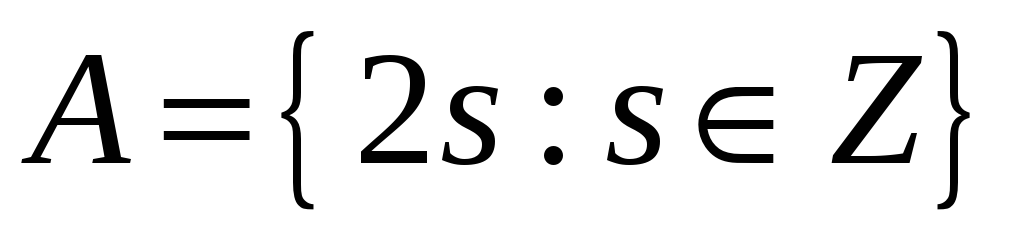 ,
,
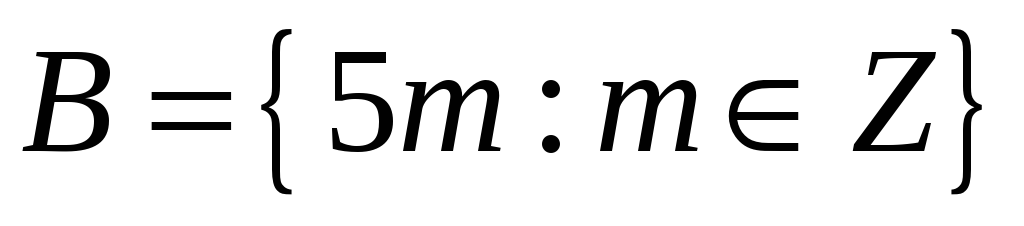 .
. -
Довести, що відображення кільця
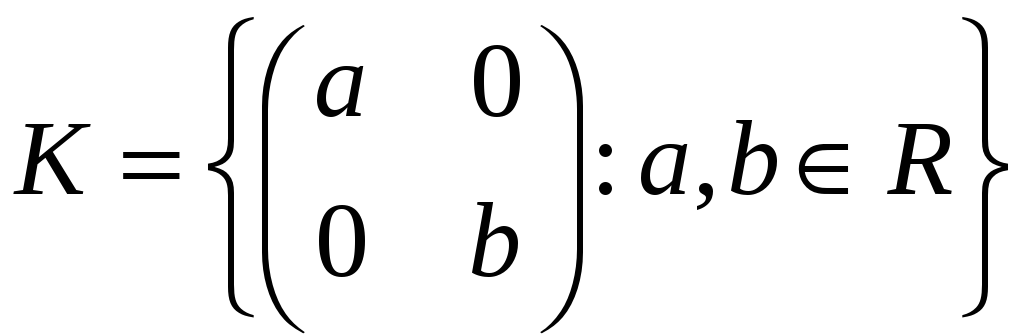 діагональних матриць на кільце
діагональних матриць на кільце
 дійсних чисел, що задається співвідношенням
дійсних чисел, що задається співвідношенням
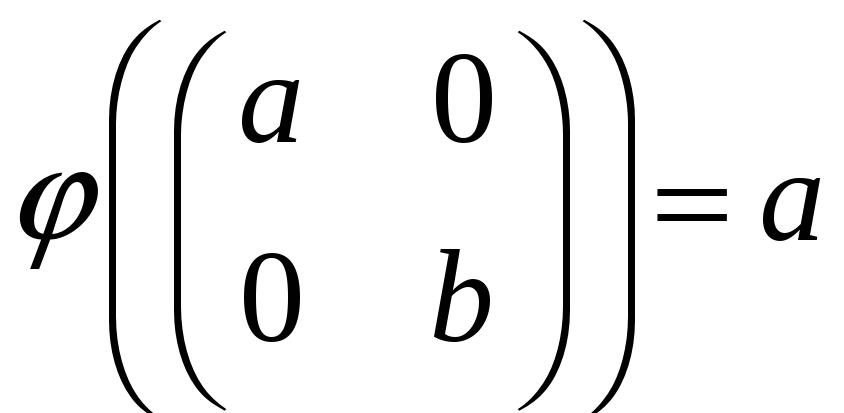 для будь-яких
для будь-яких
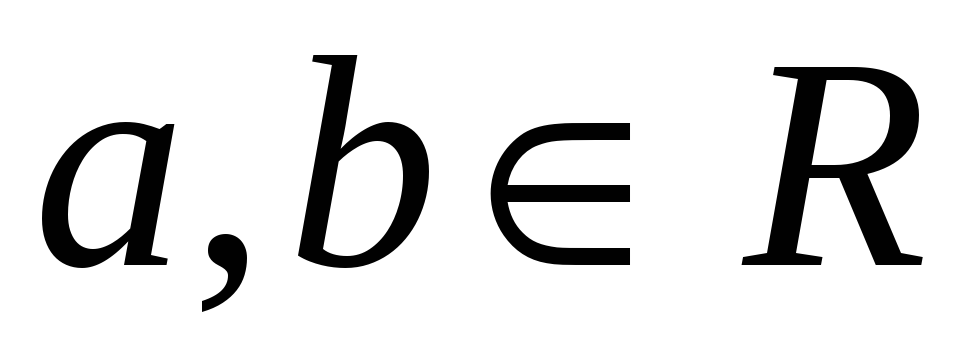 ,
є гомоморфізмом
,
є гомоморфізмом -
Довести, що
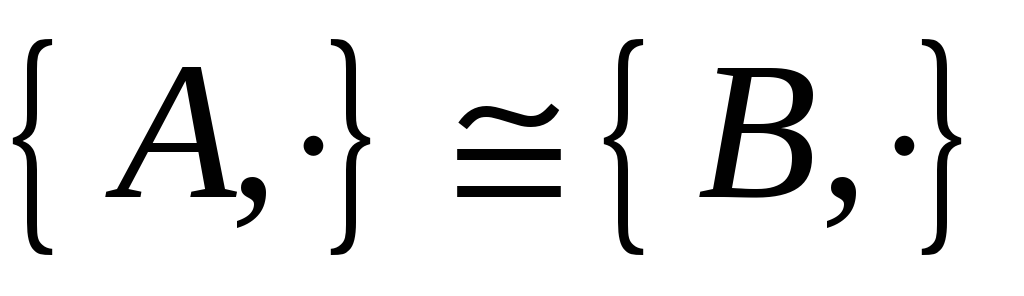 ,
де
,
де
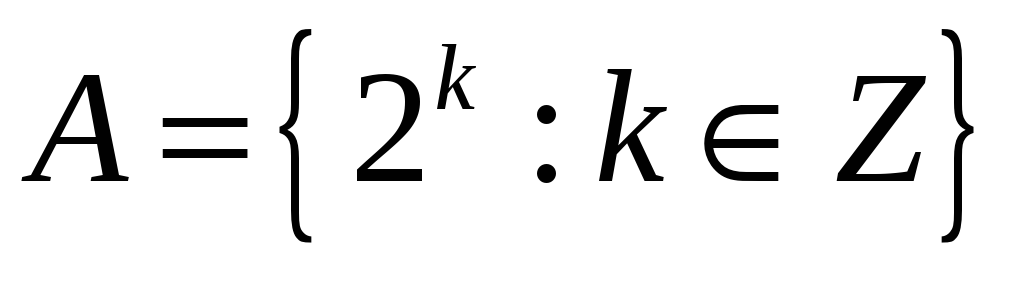 ,
,
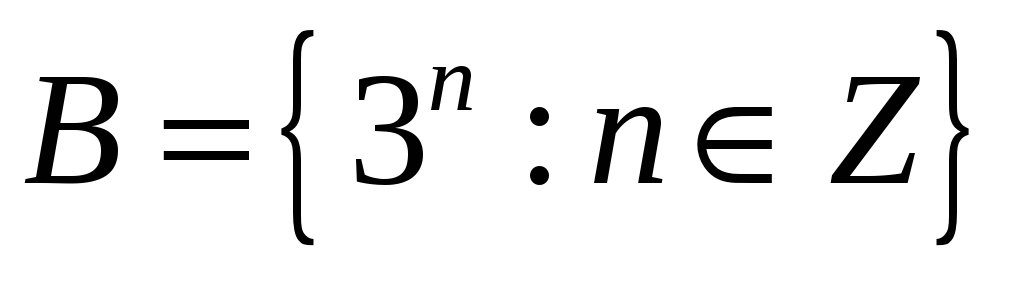 .
.
6. Векторні простори. Алгебри
Завдання
6.
Перевірити, чи утворює підпростір в
арифметичному
![]() -вимірному
просторі
-вимірному
просторі
![]() система векторів:
система векторів:
-
всі вектори, в яких перша і остання координати рівні між собою;
-
всі вектори, сума координат кожного з яких дорівнює 0;
-
всі вектори, в кожного з яких координати з парними (непарними) номерами дорівнюють 0;
-
всі вектори, в кожного з яких координати з парними номерами рівні між собою;
-
всі вектори, сума координат кожного з яких дорівнює 1;
-
всі вектори, координати яких – цілі числа;
-
всі вектори, в кожного з яких всі координати рівні між собою;
-
всі вектори, в кожного з яких кожна координата, починаючи з другої, дорівнює попередній, взятій з протилежним знаком;
-
всі вектори, в кожного з яких кожна координата, починаючи з другої, відрізняється від попередньої на множник
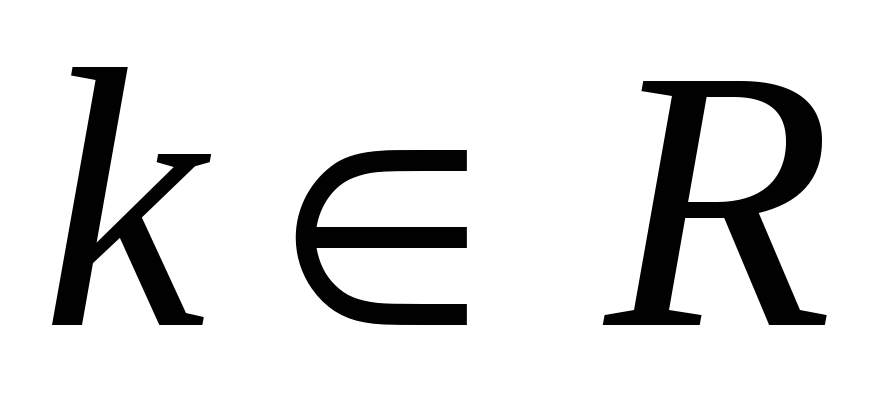 ;
; -
всі вектори, в кожного з яких кожна координата, починаючи з другої, дорівнює квадрату попередньої.
У випадку позитивної відповіді, знайти базис і розмірність відповідного підпростору.
Завдання 7.
1) В
двовимірному векторному просторі над
полем
![]() з базисом
з базисом
![]() визначено операцію множення за допомогою
таблиці множення базисних векторів:
визначено операцію множення за допомогою
таблиці множення базисних векторів:
-
.
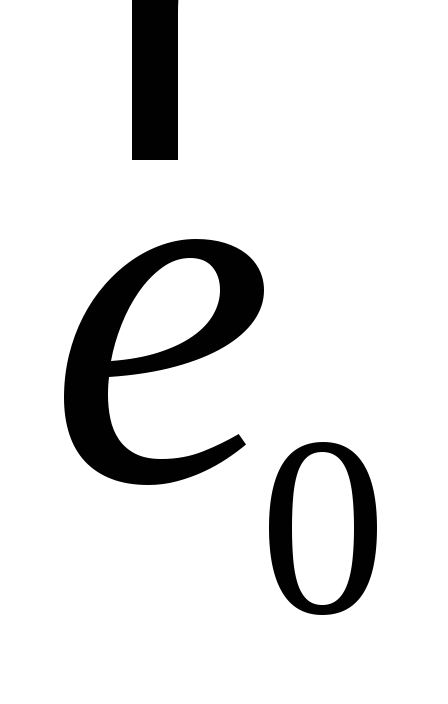

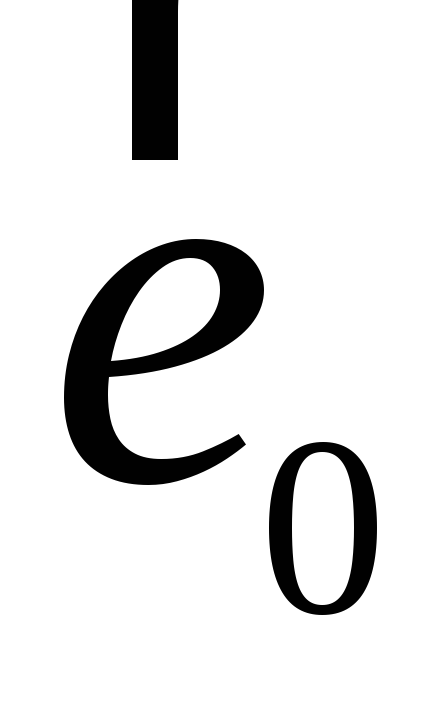
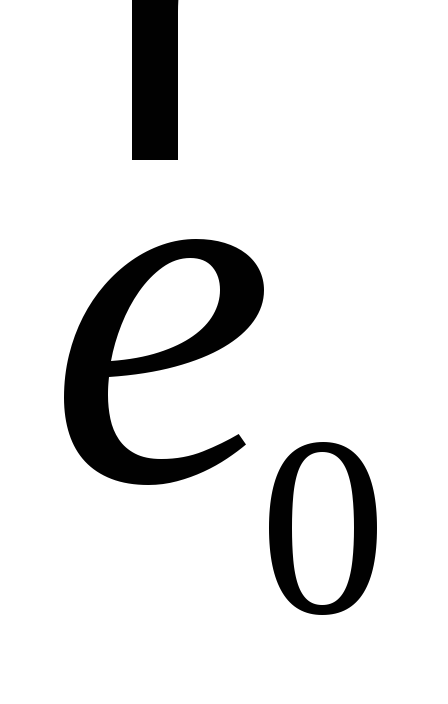
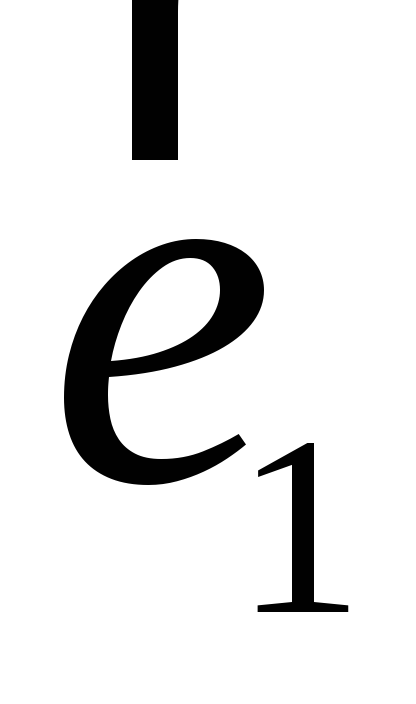

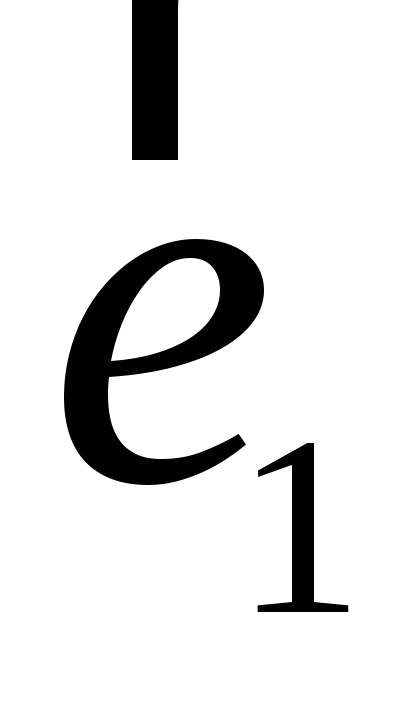
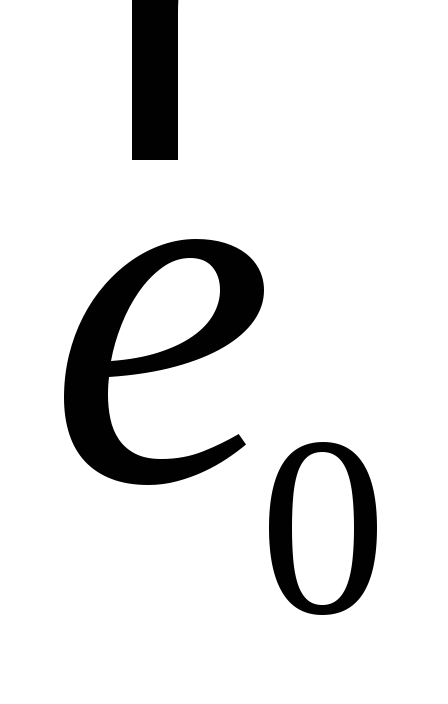
-
Знайти результат множення
 .
. -
Знайти зображення (образ) вектора
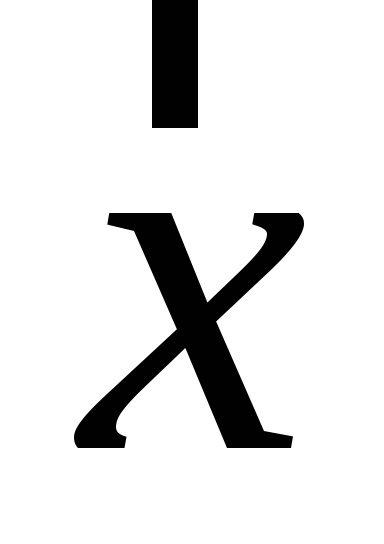 в алгебрі
в алгебрі
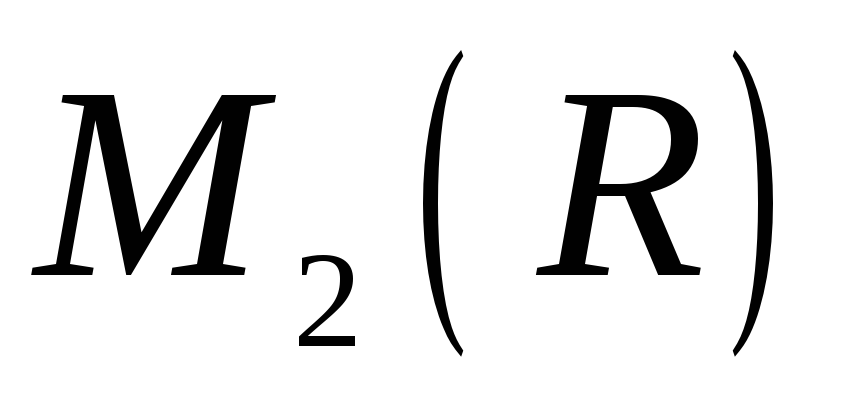 .
. -
Знайти детермінант матричного образу вектора
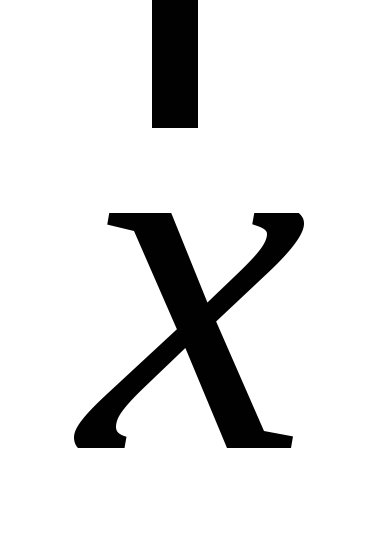 .
. -
Знайти обернений до вектора
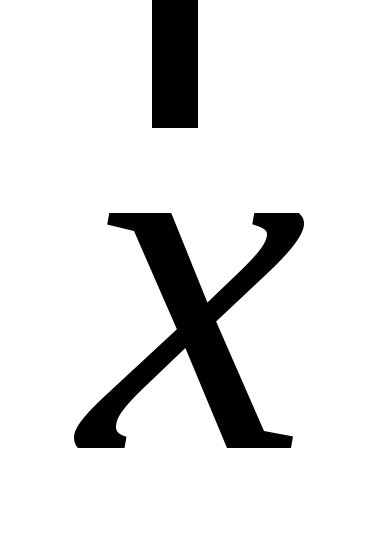 .
. -
Довести, що множина
 утворює групу, ізоморфну циклічній
групі
утворює групу, ізоморфну циклічній
групі
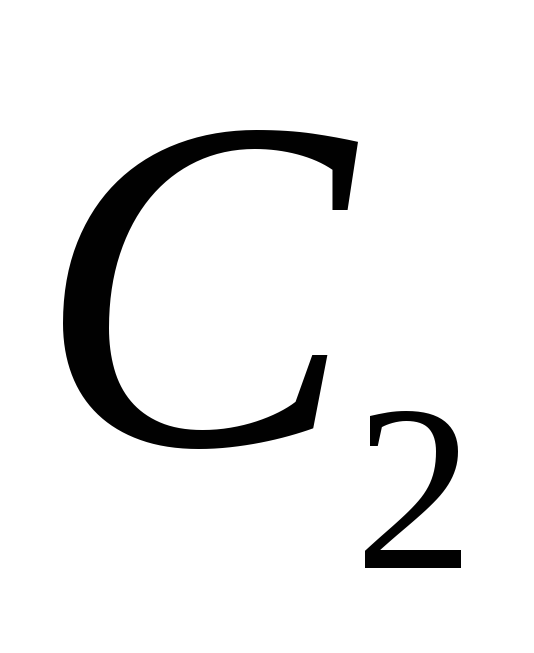 .
.
2) В
тривимірному векторному просторі над
полем
![]() з базисом
з базисом
![]() визначено операцію множення за допомогою
таблиці множення базисних векторів:
визначено операцію множення за допомогою
таблиці множення базисних векторів:
|
· |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-
Знайти результат множення
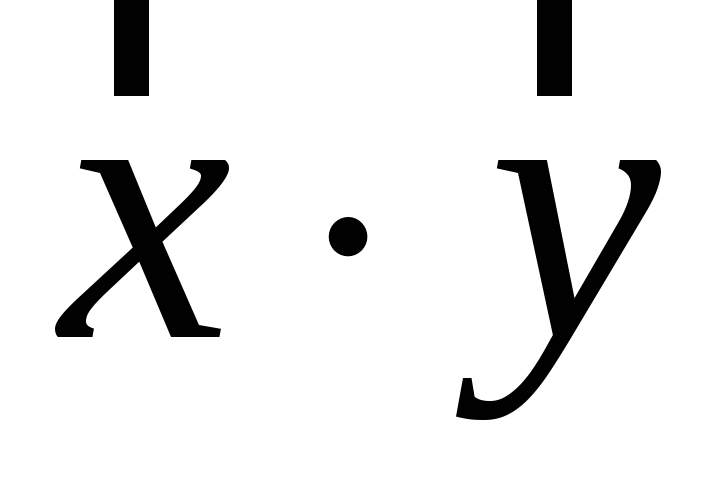 .
. -
Знайти зображення (образ) вектора
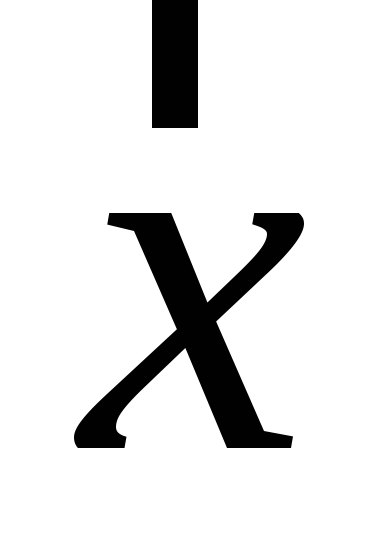 в алгебрі
в алгебрі
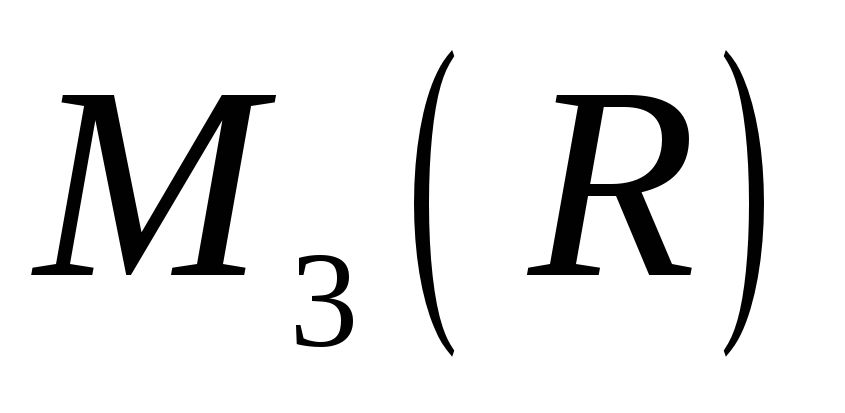 .
. -
Знайти детермінант матричного образу вектора
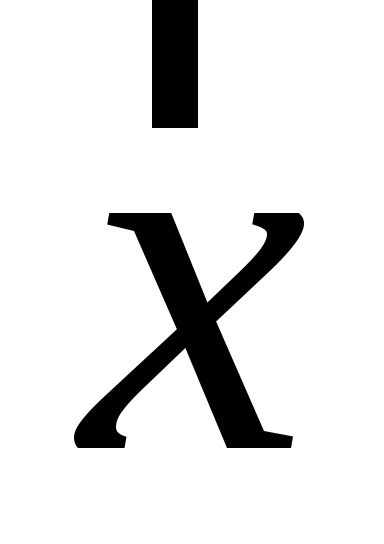 .
. -
Знайти обернений до вектора
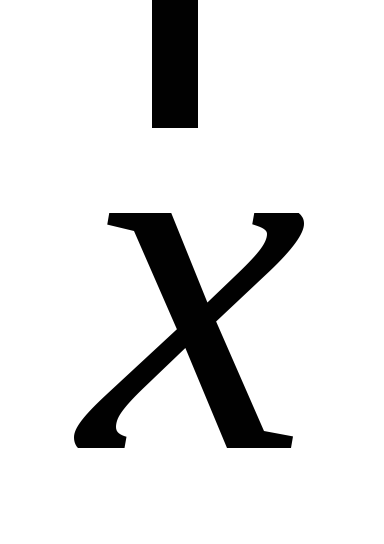 .
. -
Довести, що множина
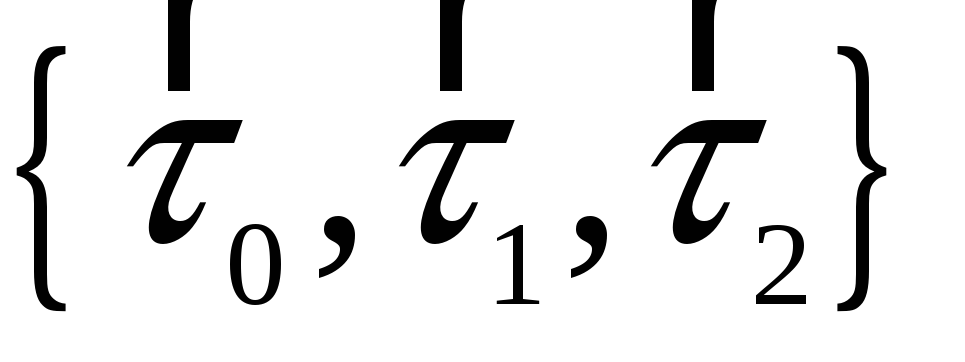 утворює групу, ізоморфну циклічній
групі
утворює групу, ізоморфну циклічній
групі
 .
Вказати одиницю і твірний цієї групи.
.
Вказати одиницю і твірний цієї групи.
3) В
тривимірному векторному просторі над
полем
![]() з базисом
з базисом
![]() визначено операцію множення за допомогою
таблиці множення базисних векторів:
визначено операцію множення за допомогою
таблиці множення базисних векторів:
-
·

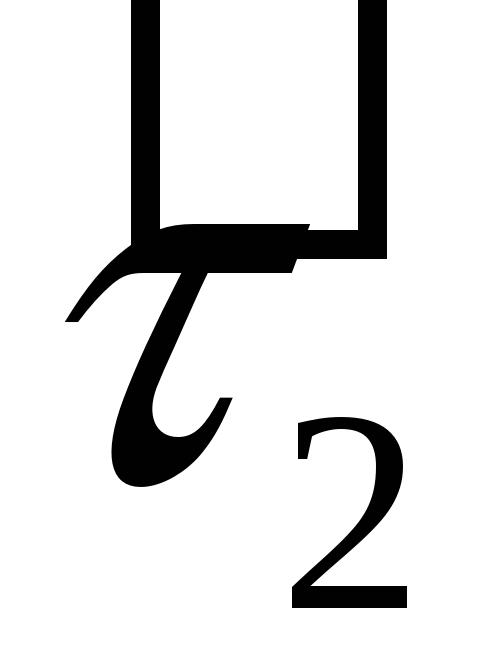



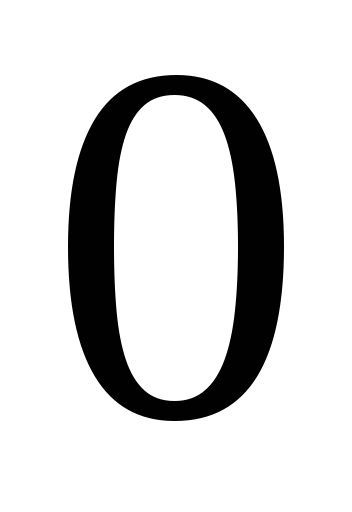

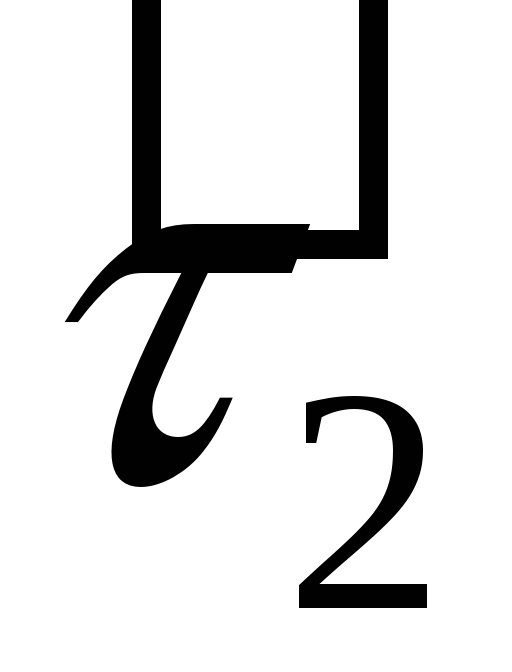
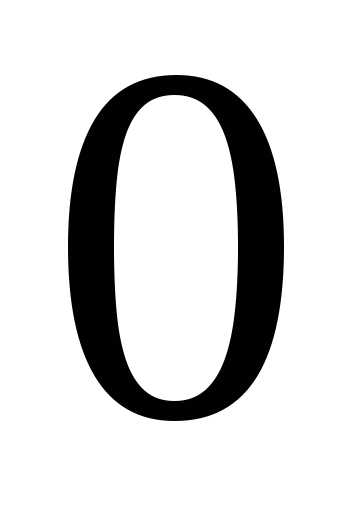
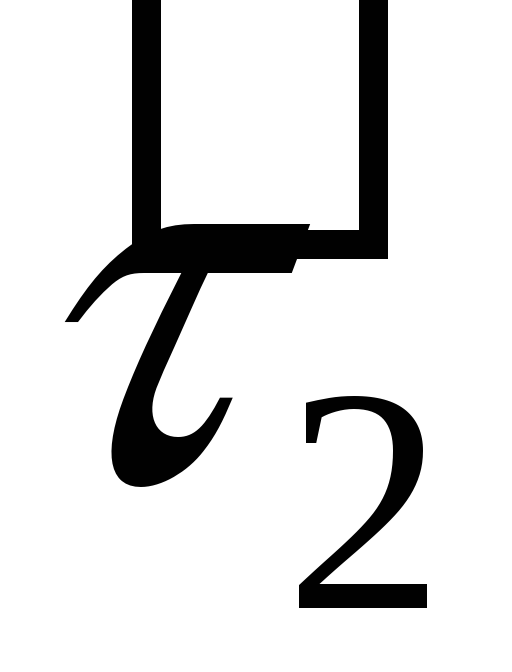
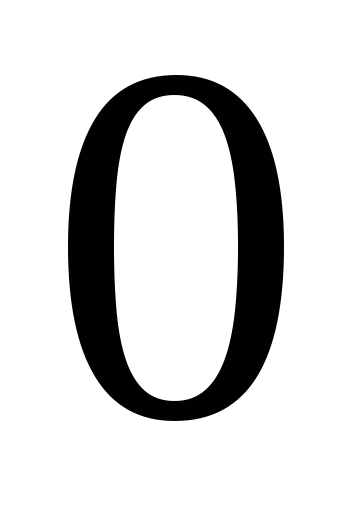




-
Знайти результат множення
 .
. -
Знайти зображення (образ) вектора
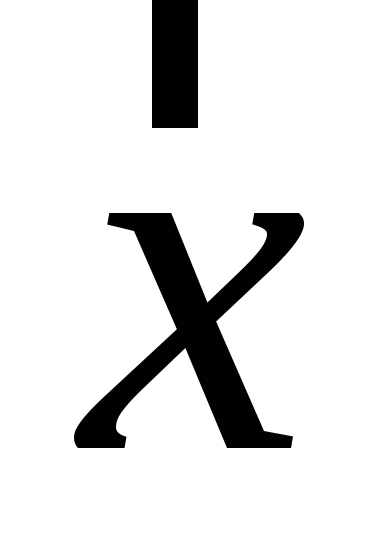 в алгебрі
в алгебрі
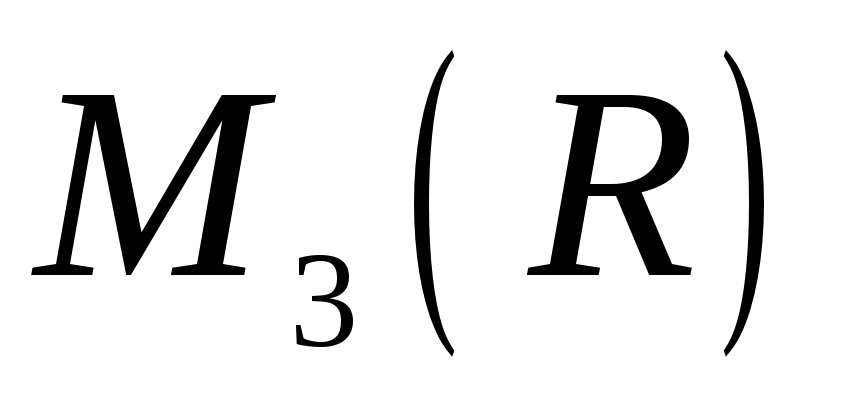 .
. -
Знайти детермінант матричного образу вектора
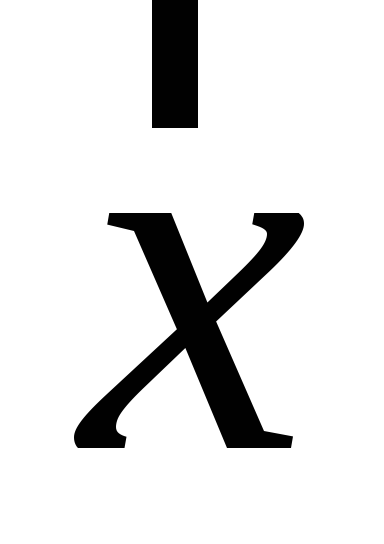 .
. -
Знайти обернений до вектора
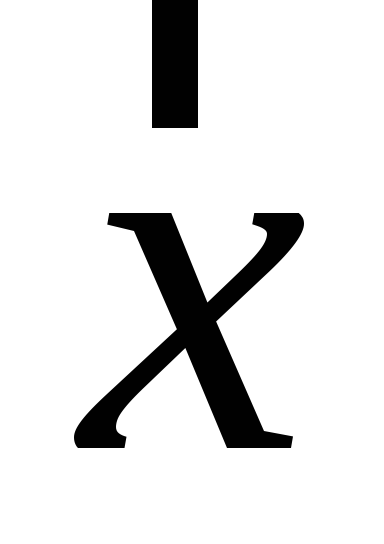 .
.
4) В
тривимірному векторному просторі над
полем
![]() з базисом
з базисом
![]() визначено операцію множення за допомогою
таблиці множення базисних векторів:
визначено операцію множення за допомогою
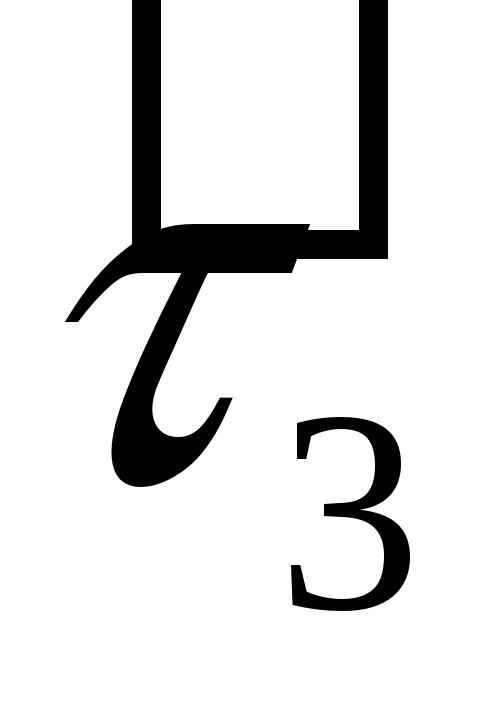
таблиці множення базисних векторів:
-
·

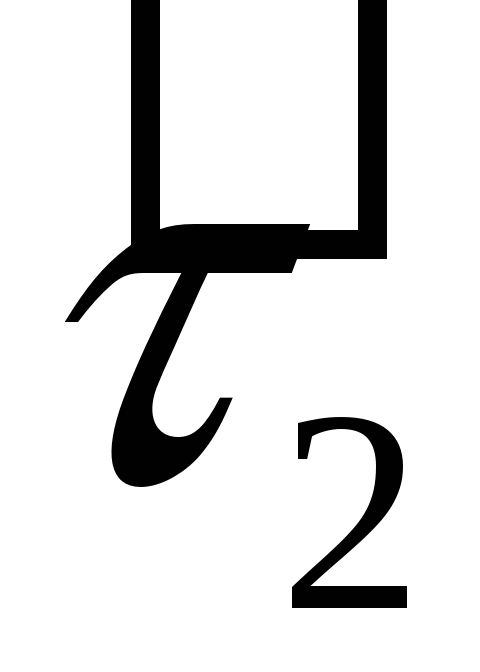



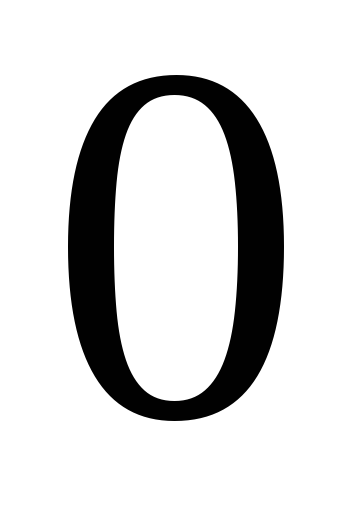
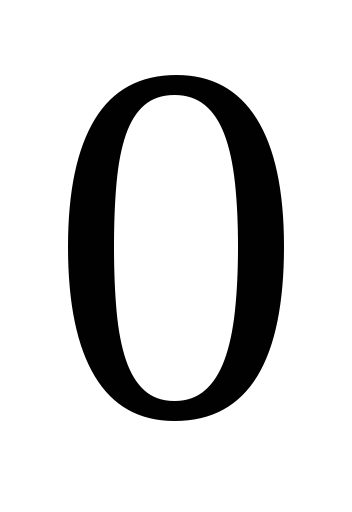
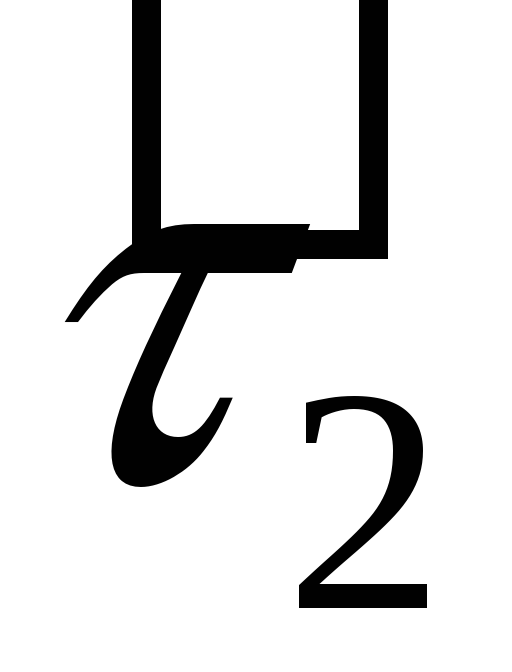
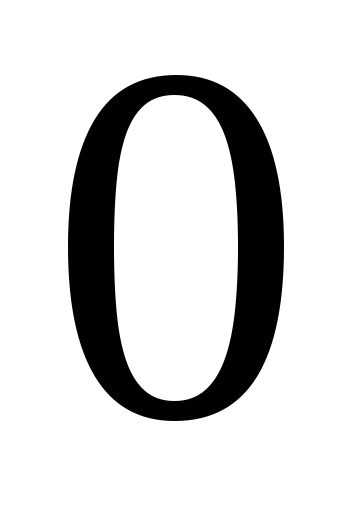
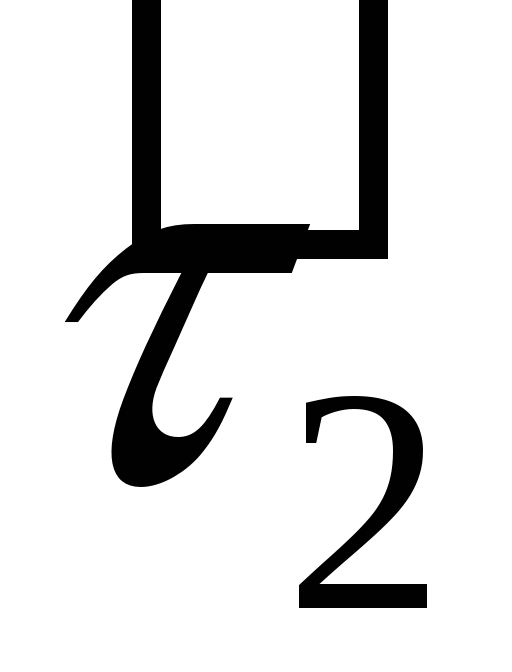

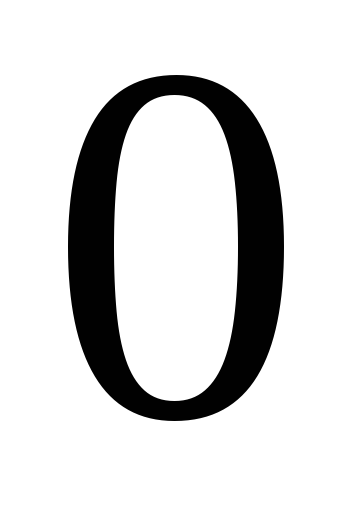

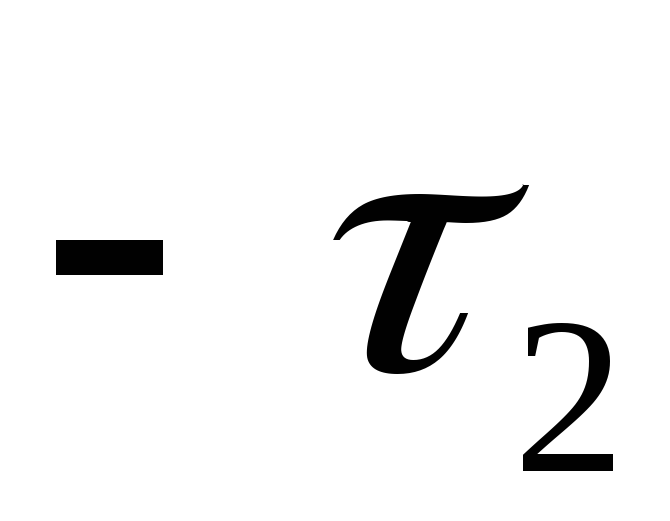
-
Знайти результат множення
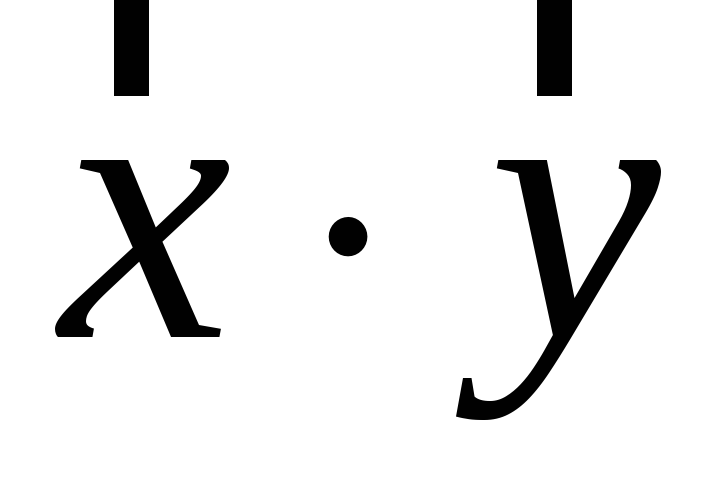 .
. -
Знайти зображення (образ) вектора
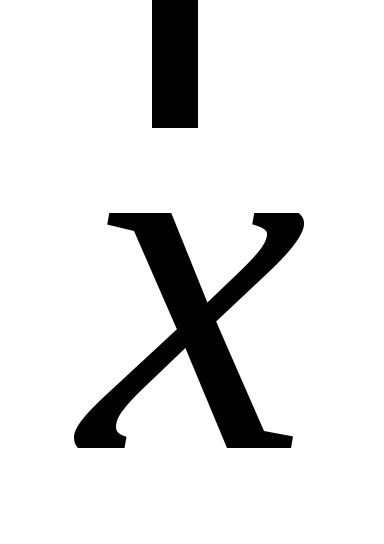 в алгебрі
в алгебрі
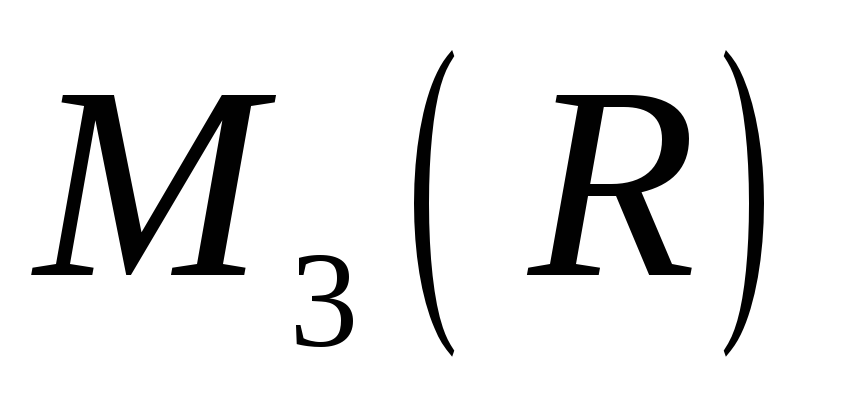 .
. -
Знайти детермінант матричного образу вектора
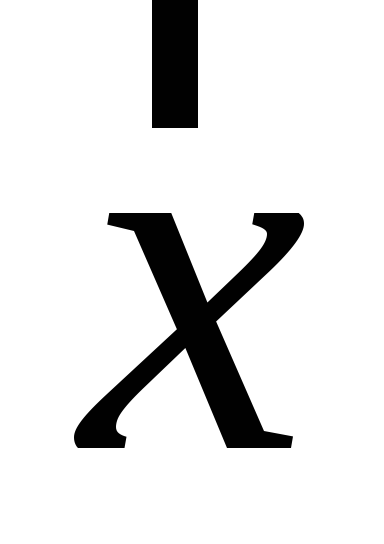 .
. -
Знайти обернений до вектора
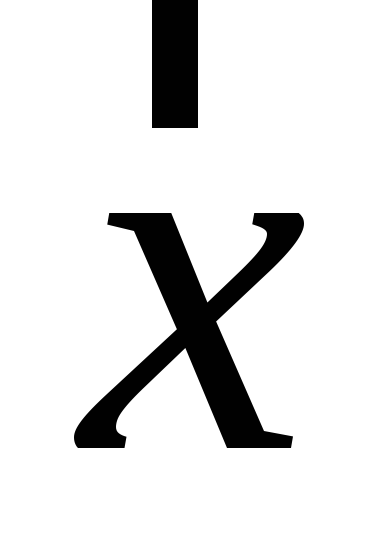 .
.
5) В
тривимірному векторному просторі над
полем
![]() з базисом
з базисом
![]() визначено операцію множення за допомогою
таблиці множення базисних векторів:
визначено операцію множення за допомогою
таблиці множення базисних векторів:
|
· |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-
Знайти результат множення
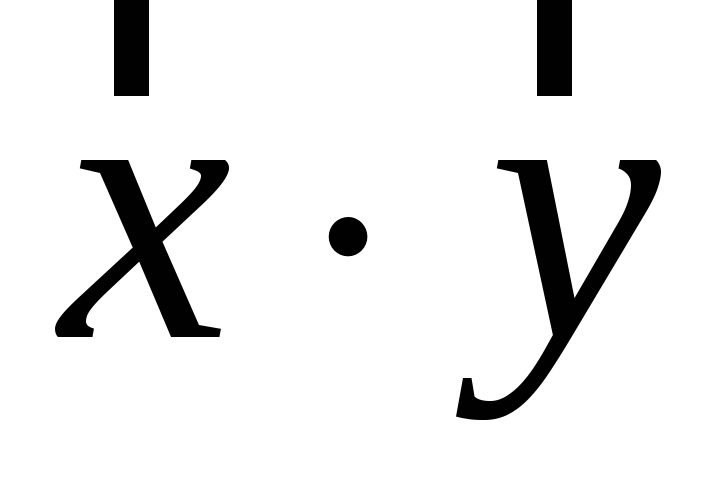 .
. -
Знайти зображення (образ) вектора
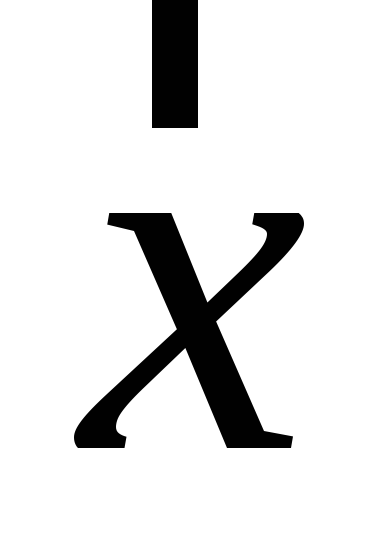 в алгебрі
в алгебрі
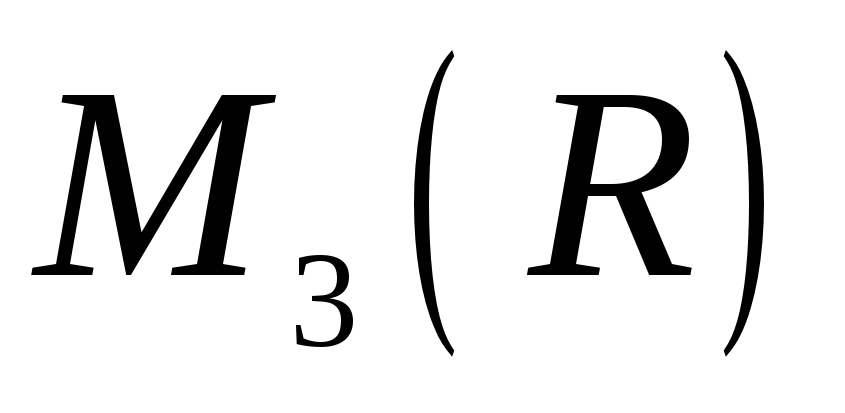 .
. -
Знайти детермінант матричного образу вектора
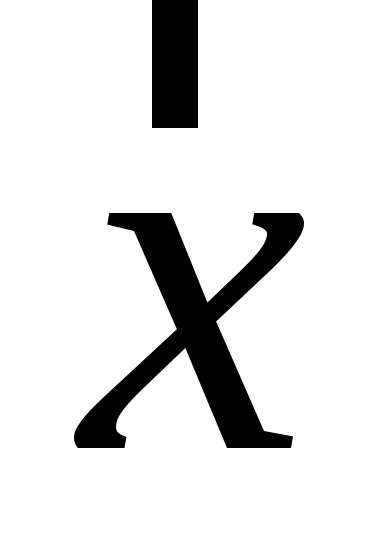 .
. -
Знайти обернений до вектора
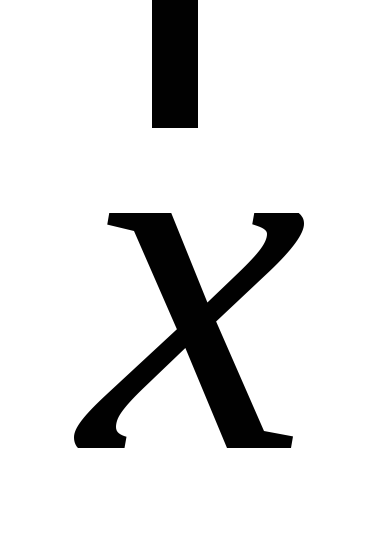 .
.
6) В
двовимірному векторному просторі над
полем
![]() з базисом
з базисом
![]() визначено операцію множення за допомогою
таблиці множення базисних векторів:
визначено операцію множення за допомогою
таблиці множення базисних векторів:
|
. |
|
|
|
|
|
|
|
|
|
0 |
-
Знайти результат множення
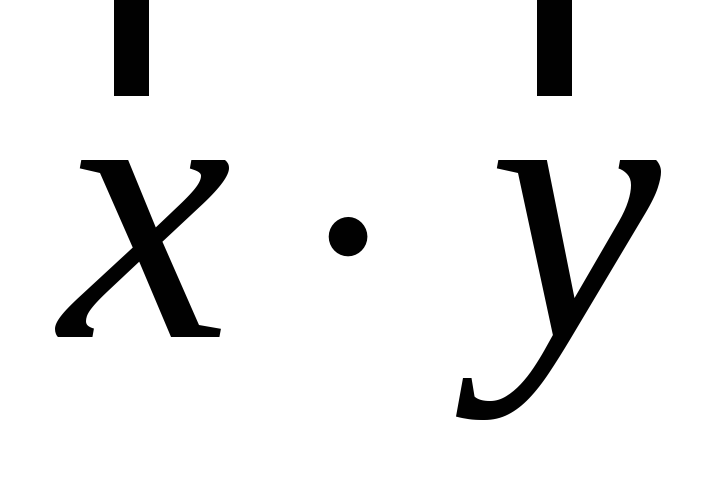 .
. -
Знайти зображення (образ) вектора
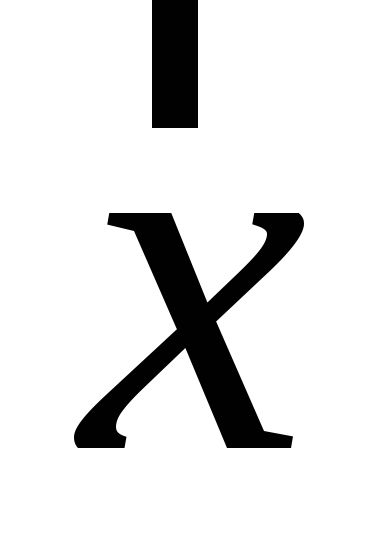 в алгебрі
в алгебрі
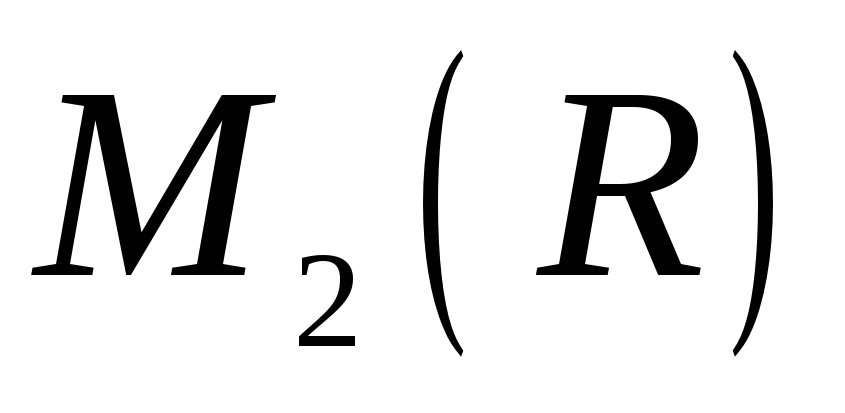 .
. -
Знайти детермінант матричного образу вектора
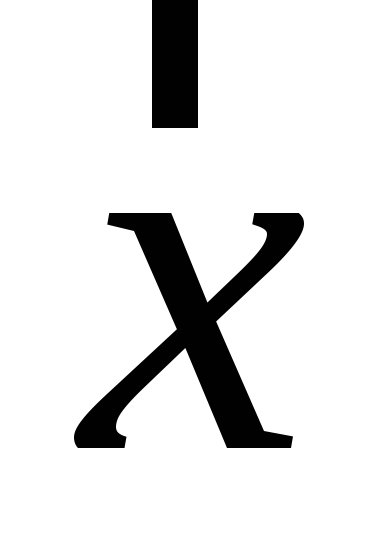 .
. -
Знайти обернений до вектора
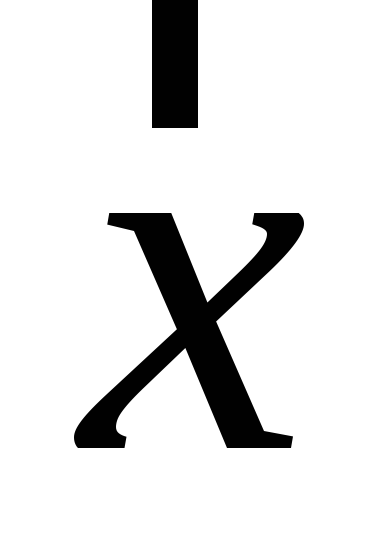 .
.
7) В
чотиривимірному векторному просторі
над полем
![]() з базисом
з базисом
![]() визначено операцію множення за допомогою
таблиці множення базисних векторів:
визначено операцію множення за допомогою
таблиці множення базисних векторів:
|
· |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-
Знайти результат множення
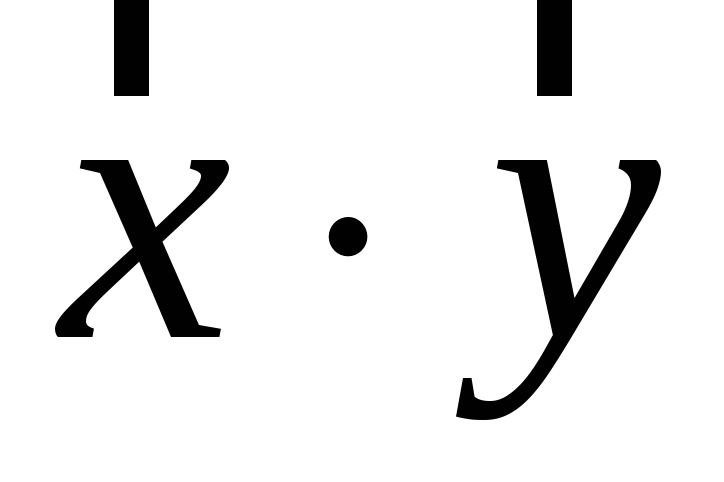 .
. -
Знайти зображення (образ) вектора
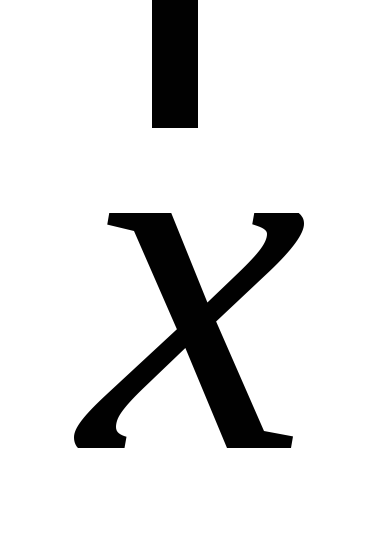 в алгебрі
в алгебрі
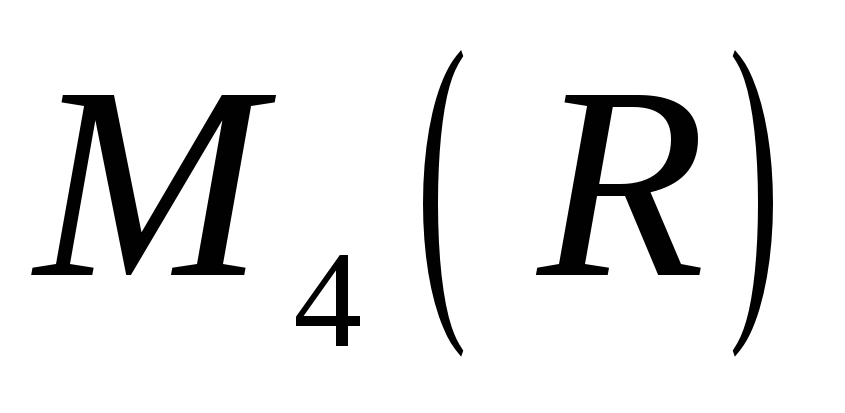 .
. -
Знайти детермінант матричного образу вектора
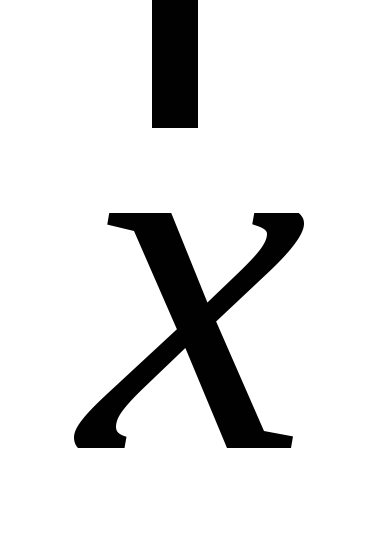 .
. -
Знайти обернений до вектора
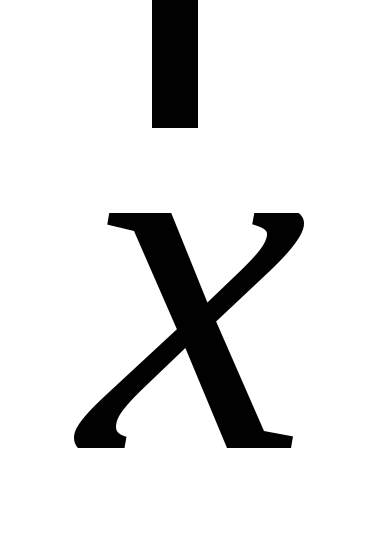 .
. -
Довести, що множина
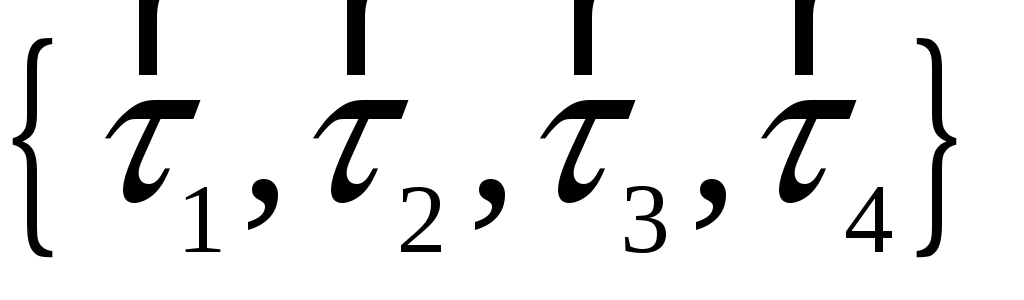 утворює групу, ізоморфну циклічній
групі
утворює групу, ізоморфну циклічній
групі
 .
Вказати одиницю і твірний цієї групи.
.
Вказати одиницю і твірний цієї групи.
8) В
тривимірному векторному просторі над
полем
![]() з базисом
з базисом
![]() визначено операцію множення за допомогою
таблиці множення базисних векторів:
визначено операцію множення за допомогою
таблиці множення базисних векторів:
|
· |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-
Знайти результат множення
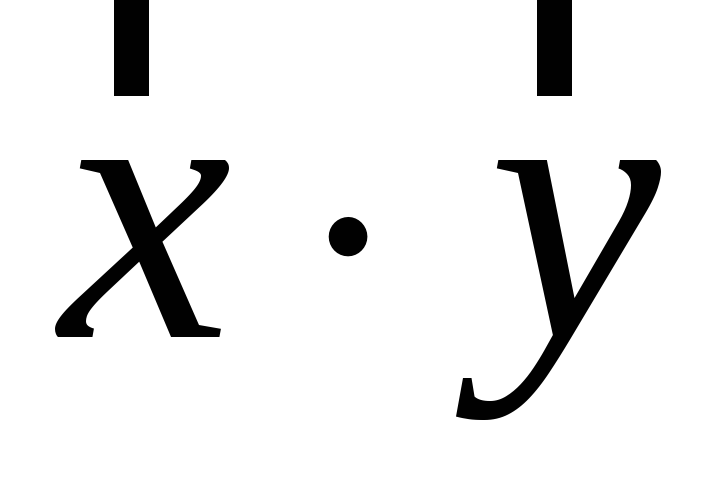 .
. -
Знайти зображення (образ) вектора
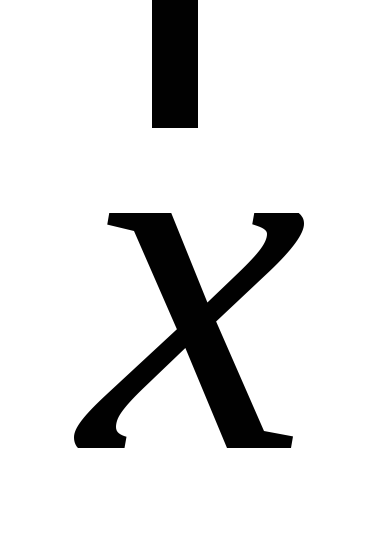 в алгебрі
в алгебрі
 .
. -
Знайти детермінант матричного образу вектора
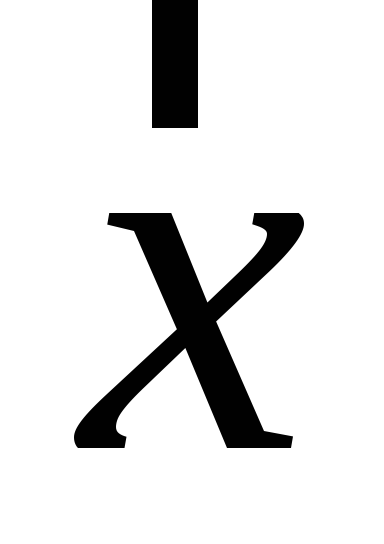 .
. -
Знайти обернений до вектора
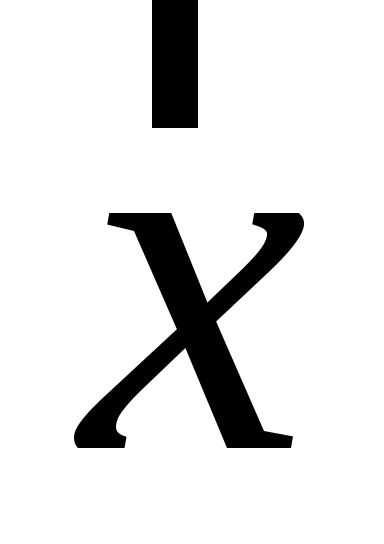 .
.
9) В
тривимірному векторному просторі над
полем
![]() з базисом
з базисом
![]() визначено операцію множення за допомогою
таблиці множення базисних векторів:
визначено операцію множення за допомогою
таблиці множення базисних векторів:
-
·





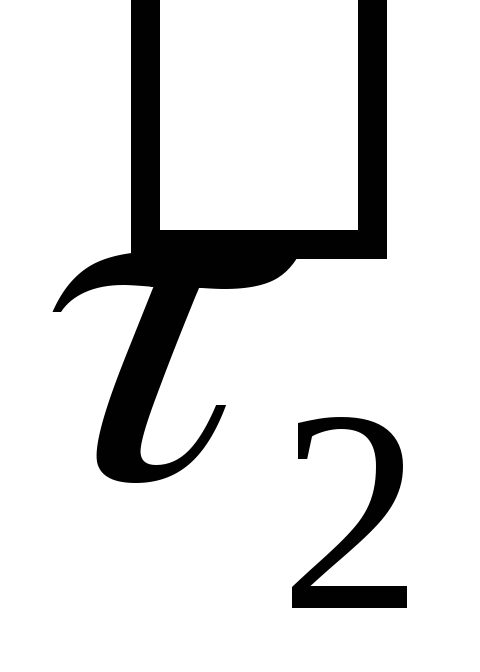

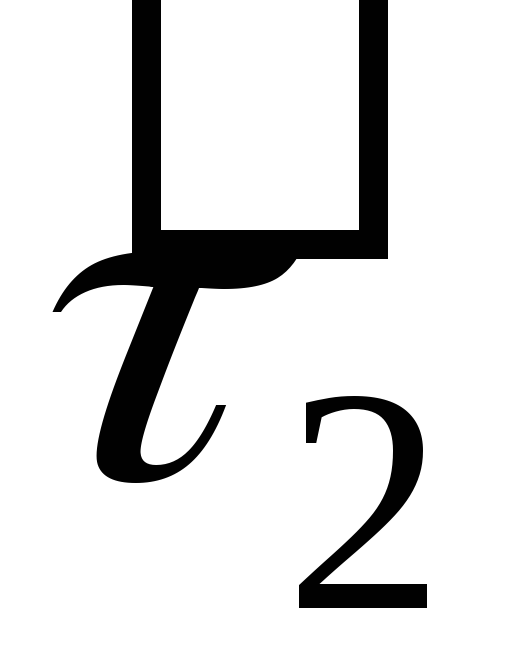
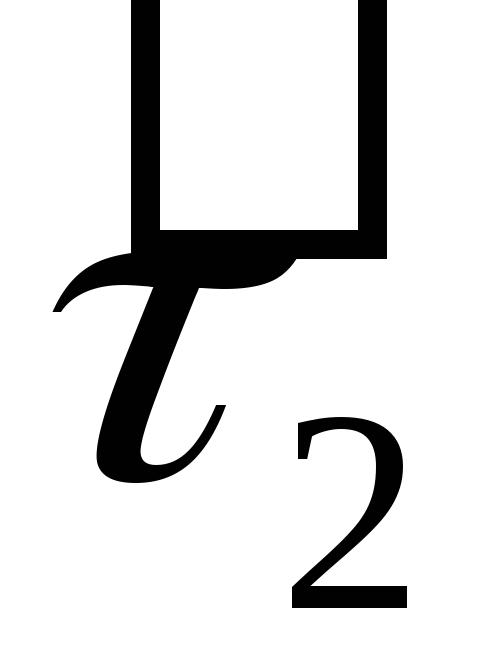
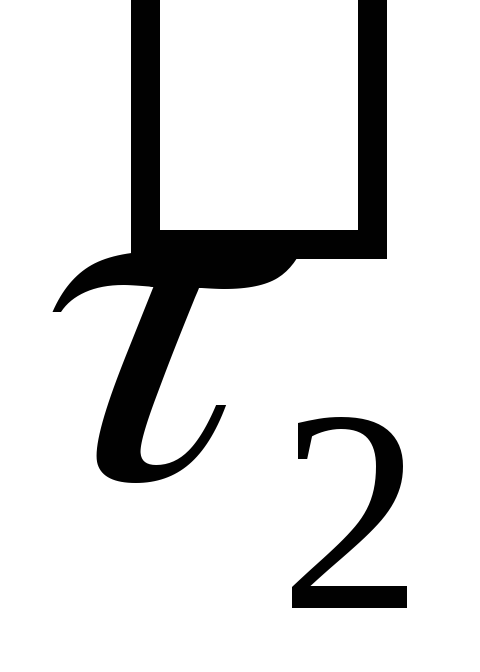
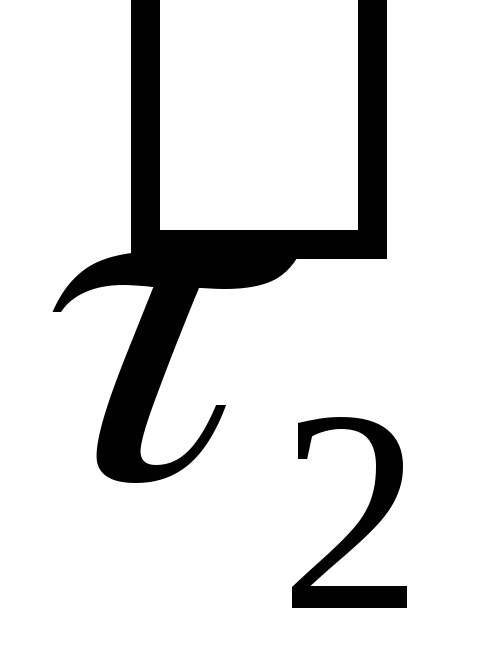




-
Знайти результат множення
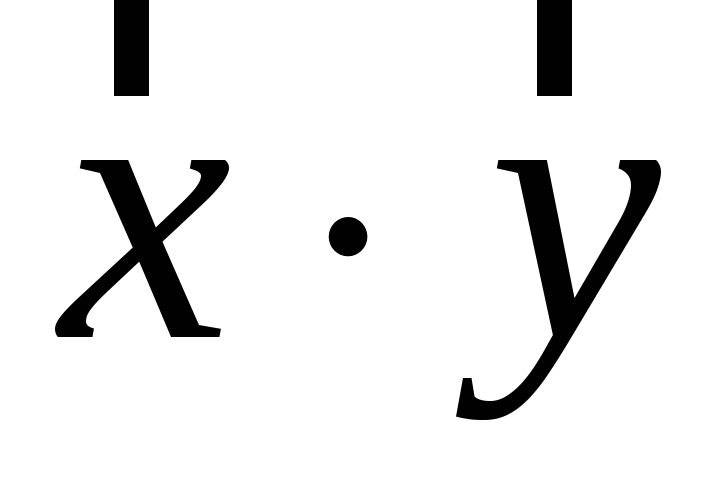 .
. -
Знайти зображення (образ) вектора
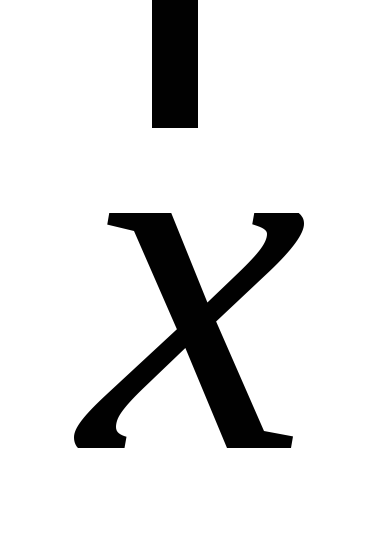 в алгебрі
в алгебрі
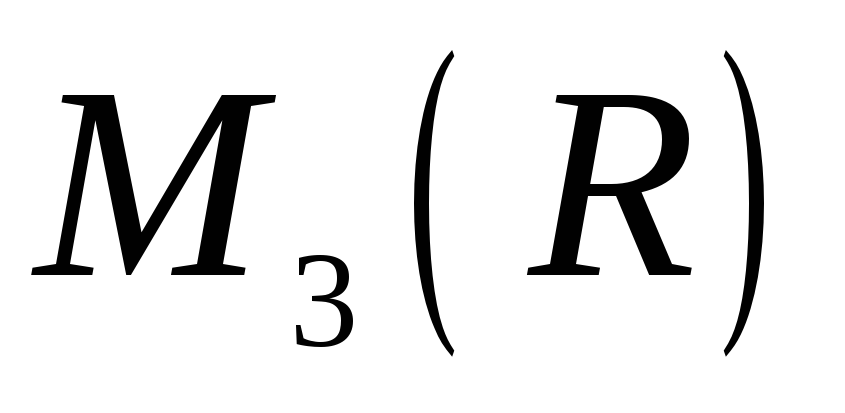 .
. -
Знайти детермінант матричного образу вектора
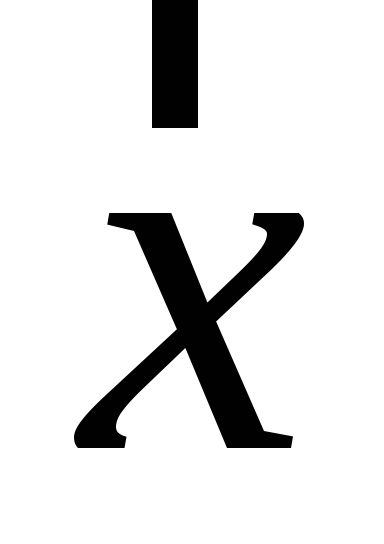 .
. -
Знайти обернений до вектора
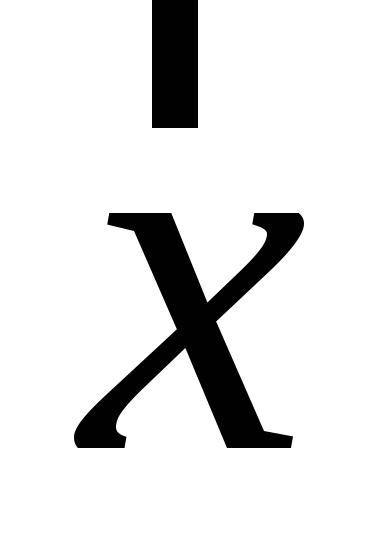 .
.
10) В
чотиривимірному векторному просторі
над полем
![]() з базисом
з базисом
![]() визначено операцію множення за допомогою
таблиці множення базисних векторів:
визначено операцію множення за допомогою
таблиці множення базисних векторів:
|
· |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-
Знайти результат множення
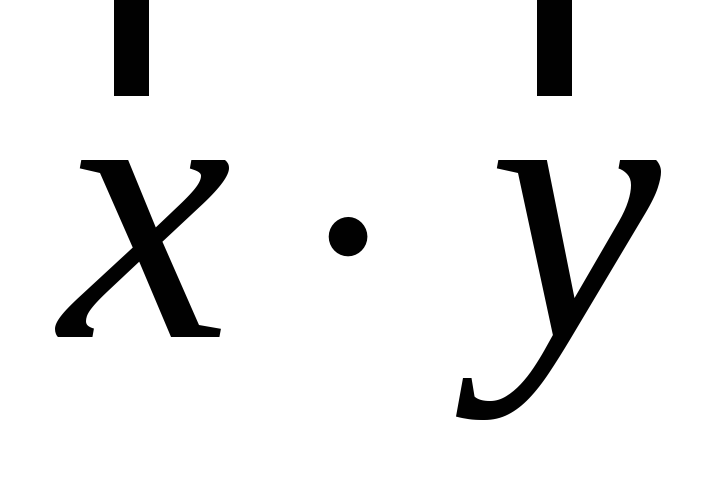 .
. -
Знайти зображення (образ) вектора
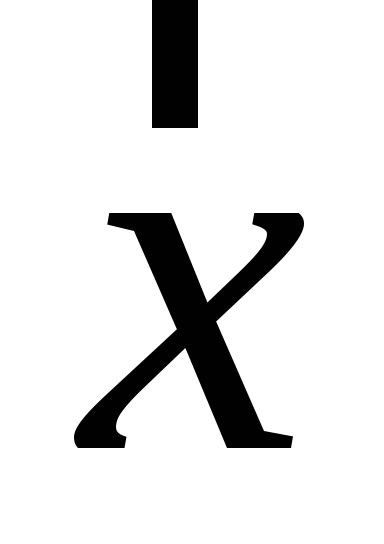 в алгебрі
в алгебрі
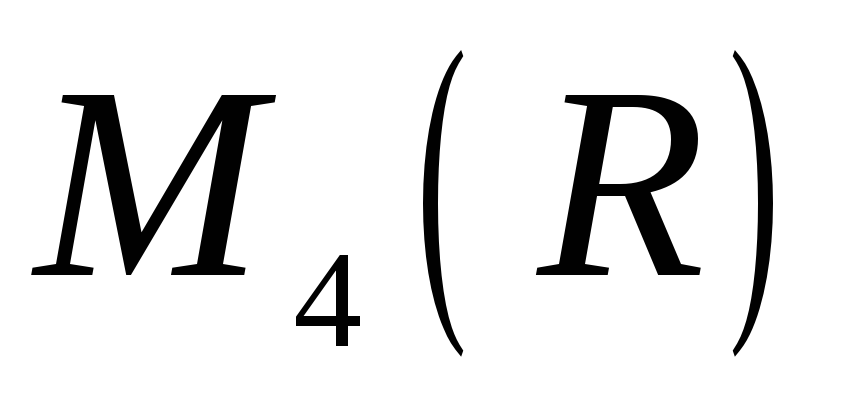 .
. -
Знайти детермінант матричного образу вектора
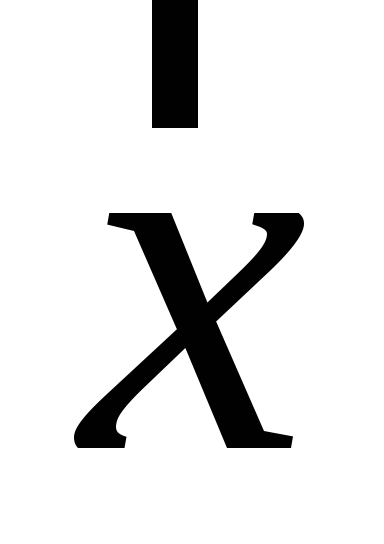 .
. -
Знайти обернений до вектора
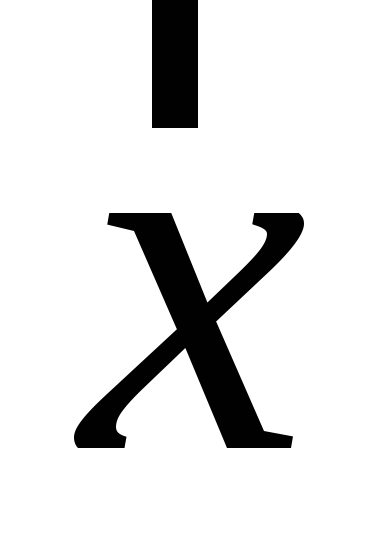 .
.
ІІІ. Порядок виконання роботи.
1. Вивчити короткі теоретичні відомості про основні алгебраїчні структури..
2. Розв’язати задачі згідно варіантам.
3. Скласти звіт, приєднавши отримані результати.
Вимоги до звіту.
У звіті мають бути приведені:
Вихідні дані (варіанти завдань);
результати і проміжні дані з необхідними поясненнями.
Література:
1. Глухов М.М., Елизаров В.П., Нечаев А.А. Алгебра. В 2-х т. Т.1 – М.: Гелиос, 2003. – 336с.
