3. Кільця

Означення. Непорожня множина , на якій визначені дві бінарні алгебраїчні операція + (додавання) і (множення), називається кільцем, якщо виконуються наступні умови (аксіоми кільця):

К1. – абелева група:

1. Операція + асоціативна:

;

2. в множині існує нульовий елемент : ;

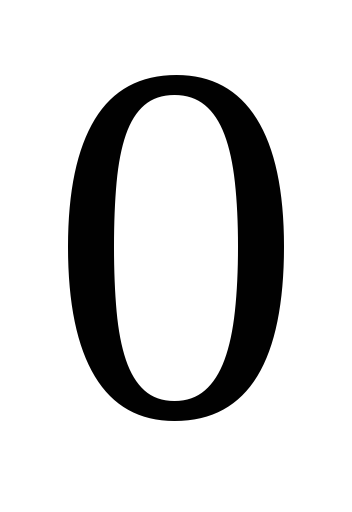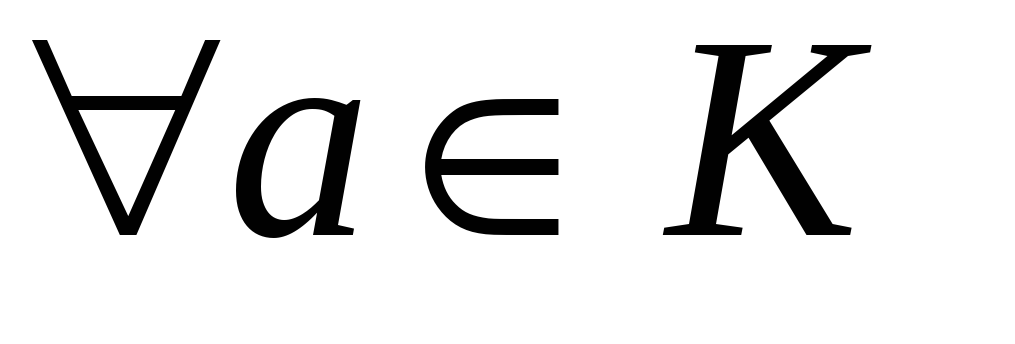
3. для кожного елемента 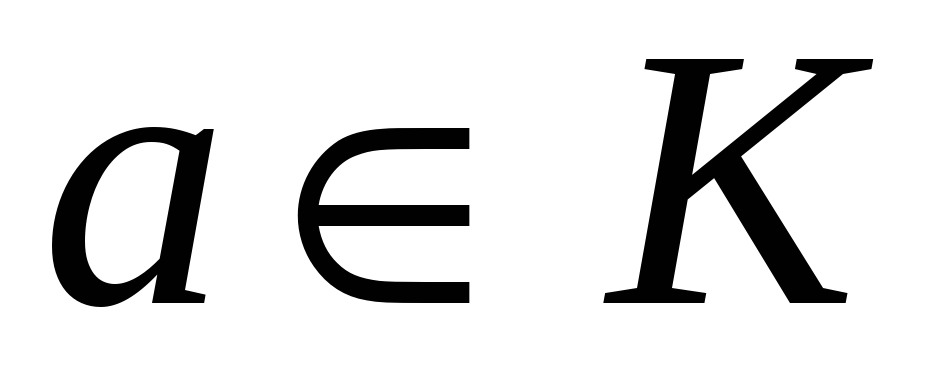існує протилежний елемент :

.

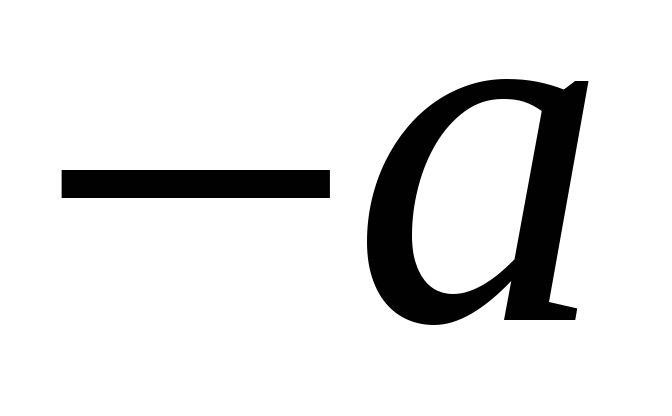4. операція + комутативна: .

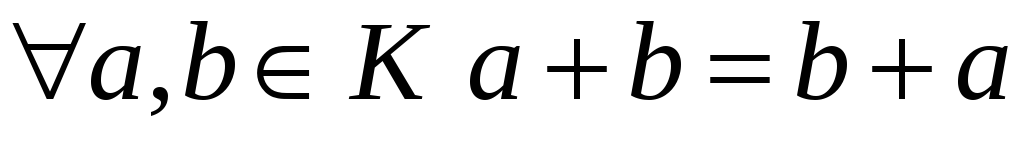К2. – півгрупа:

5. операція асоціативна: ;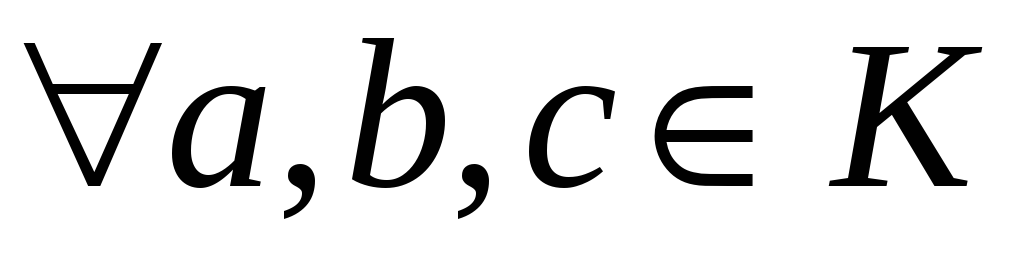

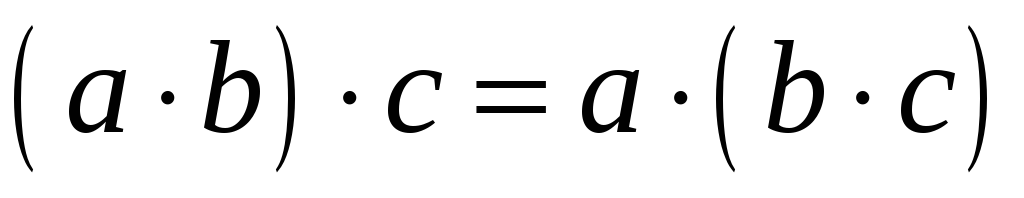К3. Операція (множення) дистрибутивна зліва і справа відносно операції+(додавання):

6. ;

;

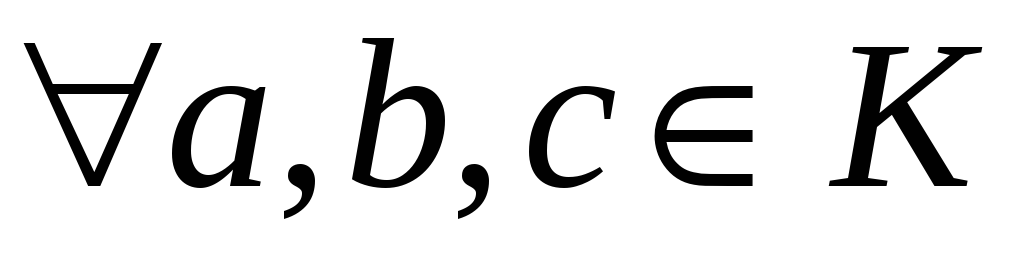
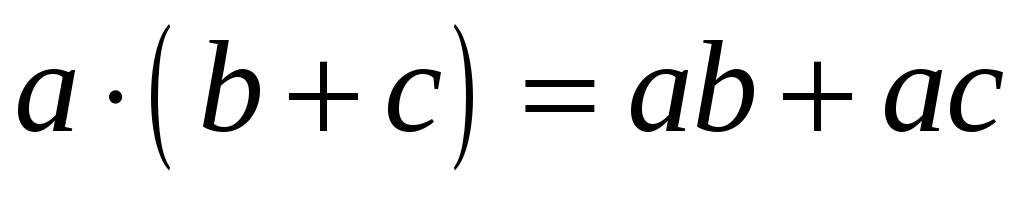Кільце позначається або просто .

Алгебраїчна структура називається адитивною групою кільця, а – його мультиплікативною півгрупою.

Означення. Кільце називається комутативним, якщо операція (множення) є комутативною, тобто

.

Означення. Кільце називається кільцем з одиницею, якщо в існує одиничний елемент , відмінний від нульового, тобто

Означення. Непорожня підмножина кільця називається підкільцем кільця , якщо є кільцем відносно алгебраїчних операцій, заданих в .

Теорема (критерій підкільця). Для того, щоб непорожня множина кільця була підкільцем цього кільця, необхідно і достатньо, щоб сума, різниця і добуток будь-яких двох елементів підмножини містилися в .

В теорії кілець особливу роль, аналогічну ролі нормальних дільників для груп, відіграють підкільця, які називаються ідеалами.

Означення. Непорожня підмножина кільця називається лівим (відповідно правим) ідеалом кільця , якщо:

1) є підгрупою адитивної групи кільця ;

2) для будь-який елементів і добуток (відповідно ) міститься в .

Підмножина кільця , яка є одночасно лівим і правим ідеалом цього кільця, називається двостороннім ідеалом або просто ідеалом кільця .

Теорема (про фактор-кільце). Множина всіх класів лишків кільця за ідеалом відносно операцій додавання і множення, визначених наступним чином:

;

,

є кільцем. Це кільце називається фактор-кільцем кільця за ідеалом (за модулем ) і позначається .

4. Поля

Означення 1. Непорожня множина , що містить не менше двох елементів, на якій визначені дві бінарні алгебраїчні операція + (додавання) і (множення), називається полем, якщо виконуються наступні умови (аксіоми поля):

1. операція + асоціативна на : ;

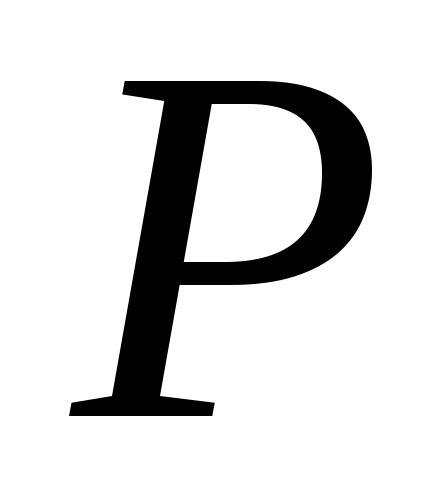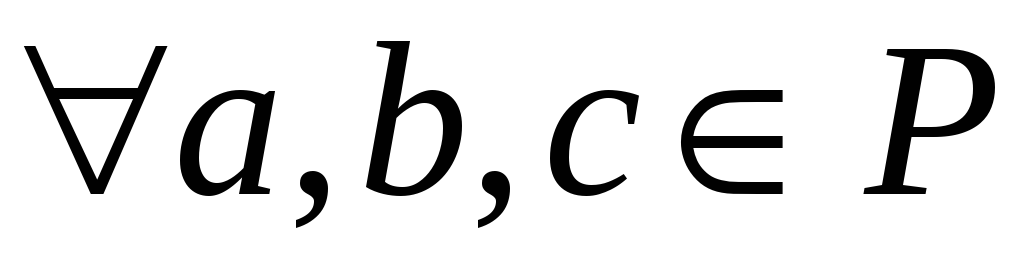
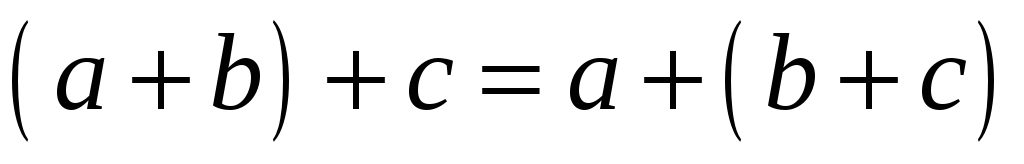2. в множині 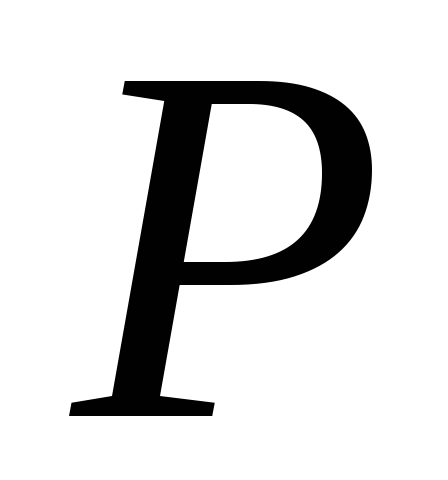існує нульовий елемент : ;

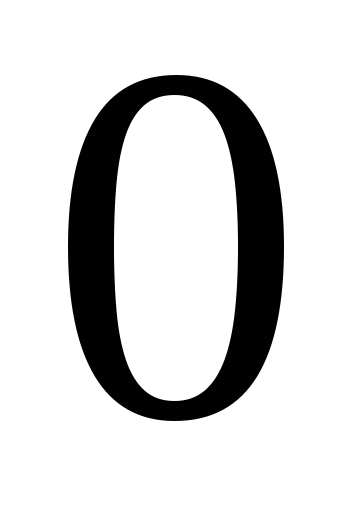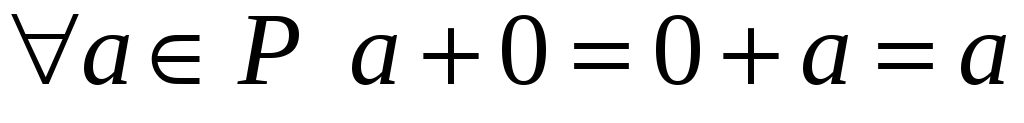3. для кожного елемента 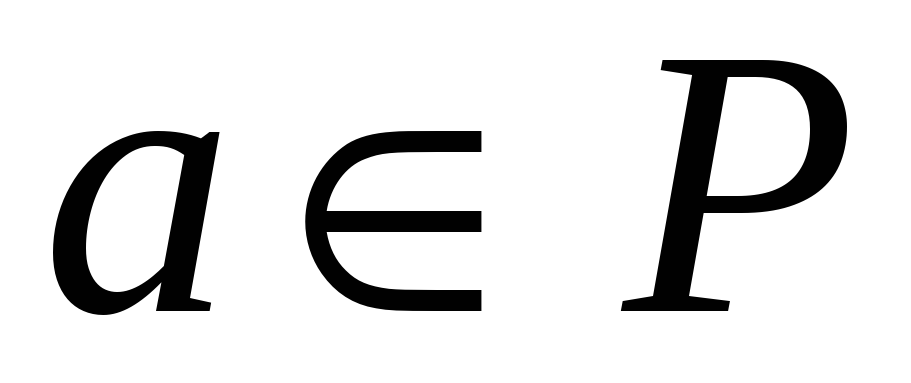існує протилежний елемент :

.

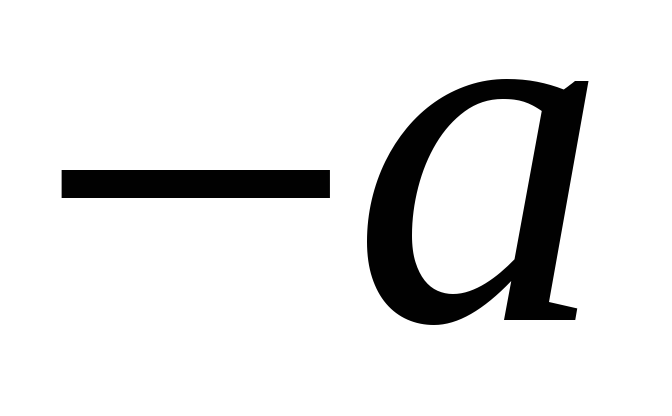4. операція + комутативна на : .

5. операція асоціативна на : ;

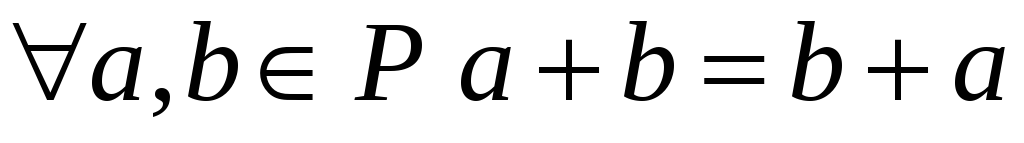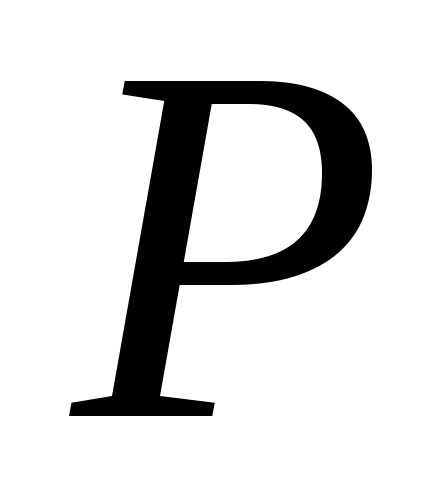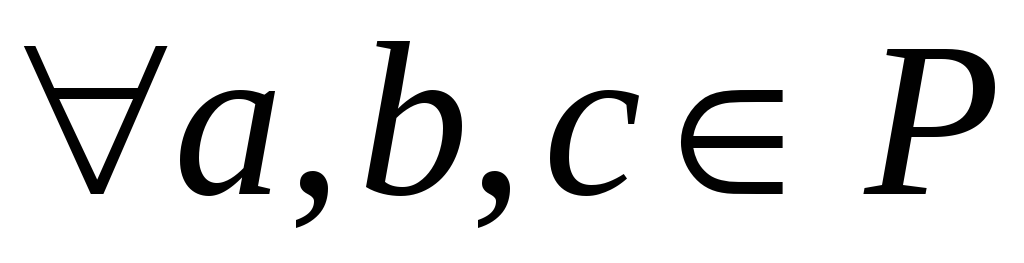
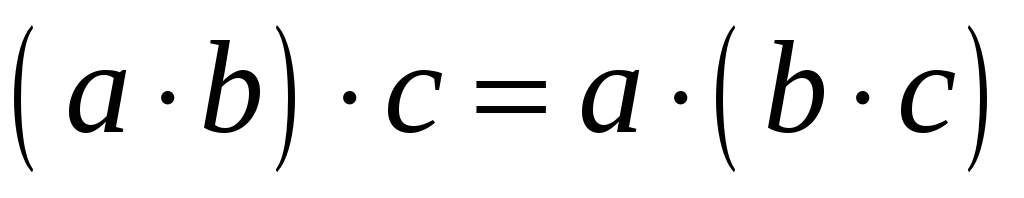6. операція дистрибутивна зліва і справа відносно операції+:

;

;

7. в множині існує одиничний елемент :

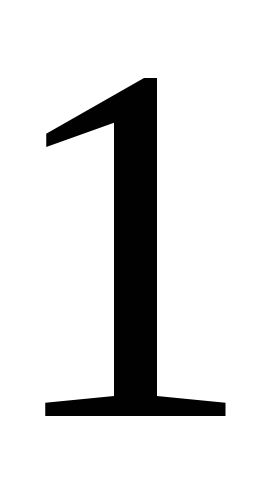8. для кожного ненульового елемента 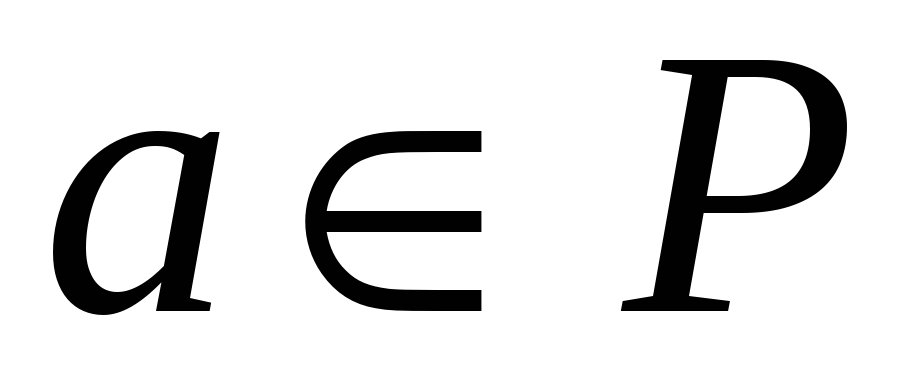існує в 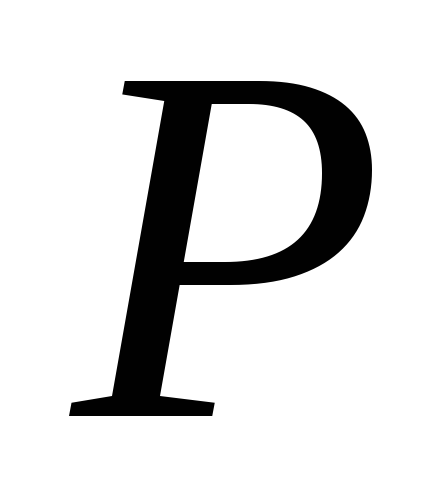обернений до нього елемент :

.

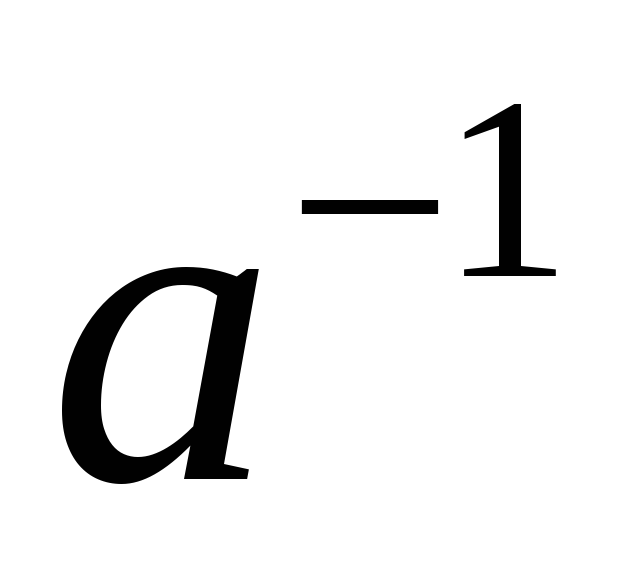9. операція комутативна на : ;

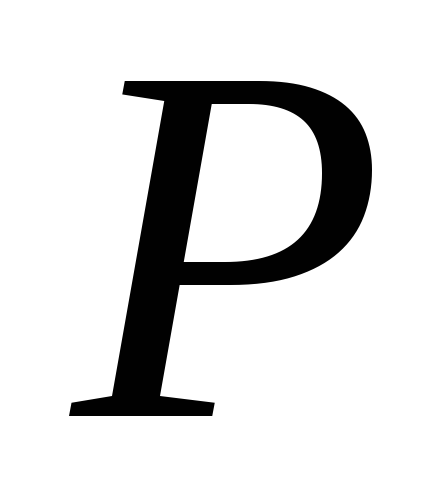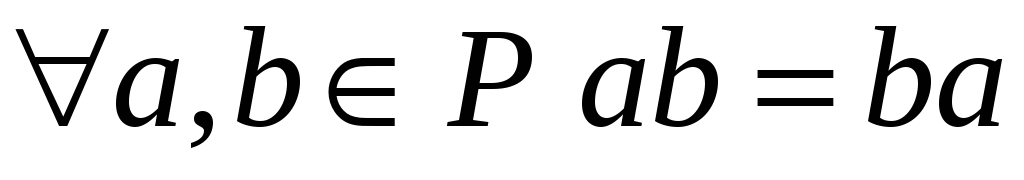Запишемо означення поля, використовуючи означення кільця.

Означення 1′. Непорожня множина , що містить не менше двох елементів, на якій визначені дві бінарні алгебраїчні операція + (додавання) і (множення), називається полем, якщо виконуються наступні умови (аксіоми поля):

1) – комутативне кільце з одиницею 1;

2) для кожного ненульового елемента існує в обернений до нього елемент :

.

Отже, поле – це комутативне кільце з одиницею 1, в якому кожний елемент має обернений.

Група називається мультиплікативною групою поля.

Поле являє собою поєднання на одній і тій самій множині двох абелевих груп – адитивної групи і мультиплікативної , зв'язаних дистрибутивним законом (тепер вже одним, з-за комутативності).

Означення. Непорожня підмножина поля називається підполем поля , якщо є полем відносно алгебраїчних операцій, заданих в .

Теорема (критерій підполя). Для того, щоб підмножина поля , яка містить не менше двох елементів, була підполем цього поля, необхідно і достатньо, щоб сума, різниця, добуток і частка будь-яких двох елементів підмножини містилися в .

Означення. Поле, яке не має ніякого власного підполя, називається простим.

Теорема. Кожне поле містить одне і тільки одне просте поле , яке ізоморфне або полю , або полю для деякого простого .

Означення. Кажуть, що поле має характеристику нуль, якщо його просте підполе ізоморфне полю . Кажуть, що поле простої (або скінченної) характеристики , якщо його просте підполе ізоморфне полю . Відповідно пишуть або .

Скінченні прості поля характеристики називають полями Галуа.