
Лабораторне заняття № 5 Тема: Скінченні поля і многочлени над скінченними полями
Мета роботи: 1. Закріпити відповідний лекційний матеріал.
2.
Навчитися
оперувати
з основними поняттями теорії
скінченних
полів і многочленів над скінченними
полями, знаходити суму, добуток, НСД
многочленів,
з’ясовувати незвідність і примітивність
многочленів
над
полем
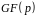 ;
будувати поля Галуа як поля многочленів
за модулем незвідного нормованого
многочлена.
;
будувати поля Галуа як поля многочленів
за модулем незвідного нормованого
многочлена.
І. Короткі теоретичні відомості (див. лекції 7,8)
1. Скінченні поля
Полем
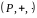 називається
множина
називається
множина
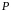 на
якій визначені дві бінарні алгебраїчні
операція + (додавання) і
на
якій визначені дві бінарні алгебраїчні
операція + (додавання) і
 (множення)
такі, що
(множення)
такі, що
– комутативне кільце з одиницею;
Для кожного ненульового елемента
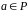 існує
в
обернений до нього елемент
існує
в
обернений до нього елемент
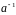 :
:
 .
.
Отже, поле – це комутативне кільце з одиницею, в якому кожний елемент має обернений.
Поле
являє
собою поєднання на одній і тій самій
множині двох абелевих груп – адитивної
групи
і мультиплікативної
 ,
зв'язаних дистрибутивним законом (тепер
вже одним, з-за комутативності).
,
зв'язаних дистрибутивним законом (тепер
вже одним, з-за комутативності).
Якщо множина скінченна, поле називається скінченним. Число елементів множини називається порядком поля.
Приклад
скінченного
поля – кільце
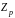 класів лишків цілих чисел за модулем
простого числа
класів лишків цілих чисел за модулем
простого числа
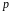 .
Елементами кільця
є
.
Елементами кільця
є
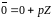 ,
,
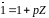 ,
,
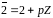 ,
…,
,
…,
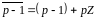 ,
де
,
де
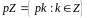 .
В кільці класів лишків звичайно оперують
з фіксованою множиною представників
за модулем
.
В кільці класів лишків звичайно оперують
з фіксованою множиною представників
за модулем
 .
.
Скінченні
поля легко будувати на базі кілець
класів лишків
за даним простим модулем наступним
чином. Для
простого числа
позначимо через
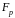 множину
множину
 .
Визначимо відображення
.
Визначимо відображення
 ,
де
,
де
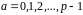 (
(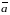 – класи лишків за модулем
).
Тоді множина
із
структурою поля, індукованою відображенням
– класи лишків за модулем
).
Тоді множина
із
структурою поля, індукованою відображенням
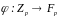 ,
також утворює скінченне поле, яке
називається полем
Галуа порядку
Відображення
є ізоморфізмом,
оскільки
зберігає операції:
,
також утворює скінченне поле, яке
називається полем
Галуа порядку
Відображення
є ізоморфізмом,
оскільки
зберігає операції:
 .
Нулем
скінченного поля
.
Нулем
скінченного поля
 буде нуль 0,
а
одиницею – одиниця 1
і
його структура співпадає із структурою
поля
.
буде нуль 0,
а
одиницею – одиниця 1
і
його структура співпадає із структурою
поля
.
При обчисленнях з елементами поля використовується арифметика цілих чисел із зведенням за модулем .
Арифметика над скінченними полями широко застосовується в криптографії і є основою багатьох криптосистем. Елементами таких полів є тільки скінченні числа, при операціях над якими відсутні похибки заокруглення.
Характеристикою
поля
називається найменше натуральне число
 таке, що для одиниці 1 поля
таке, що для одиниці 1 поля
 .
Характеристика поля позначається
.
Характеристика поля позначається
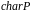 .
Якщо поле має додатну характеристику
,
то
.
Якщо поле має додатну характеристику
,
то
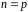 ,
де
– просте число. Отже,характеристика
будь-якого поля є або 0, або просте число
.
В першому випадку поле
містить просте підполе, ізоморфне полю
раціональних
чисел
,
де
– просте число. Отже,характеристика
будь-якого поля є або 0, або просте число
.
В першому випадку поле
містить просте підполе, ізоморфне полю
раціональних
чисел
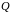 ,
в другому містить просте (тобто таке,
що не має ніякого власного підполя)
підполе, ізоморфне полю
.
Відповідно
пишуть
,
в другому містить просте (тобто таке,
що не має ніякого власного підполя)
підполе, ізоморфне полю
.
Відповідно
пишуть
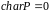 або
або
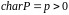 .
.
Характеристика скінченного поля – просте число.
Будь-яке скінченне поле характеристики містить просте підполе з елементів і є скінченним розширенням цього підполя.
Теорема.
Нехай
–
скінченне поле. Тоді воно складається
з
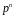 елементів,
де
просте
число, що є характеристикою поля
,
а
елементів,
де
просте
число, що є характеристикою поля
,
а
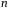 –
натуральне число, що є степенем поля
над його простим підполем.
–
натуральне число, що є степенем поля
над його простим підполем.
Розглянемо питання про число елементів скінченного поля.
Лема
1.
Нехай
–
скінченне поле, що містить підполе
 з
з
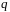 елементів.
Тоді
складається
з
елементів.
Тоді
складається
з
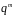 елементів, де
елементів, де
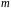 – степінь
поля
над
,
тобто розмірність векторного простору
над
полем
.
– степінь
поля
над
,
тобто розмірність векторного простору
над
полем
.
Теорема. Нехай – скінченне поле. Тоді воно складається з елементів, де просте число, що є характеристикою поля , а – натуральне число, що є степенем поля над його простим підполем.
Доведення. Оскільки поле скінченне, то його характеристика є деяке просте число . Тому просте підполе поля ізоморфне і, значить, містить елементів і, отже, згідно лемі 1, поле містить елементів. □
Лема
2.
Якщо
–
скінченне поле з
елементів,
то кожний елемент
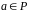 задовольняє рівності
задовольняє рівності
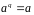 .
.
Означення.
Поле
називається
полем
розкладання
многочлена
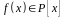 над полем
,
якщо
над полем
,
якщо
 і над полем
многочлен
і над полем
многочлен
 розкладається на лінійні множники.
розкладається на лінійні множники.
Лема
3.
Якщо
–
скінченне поле з
елементів
і
–
підполе поля
,
то многочлен
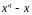 з
кільця
з
кільця
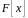 цілком
розкладається в
цілком
розкладається в
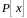 наступним чином:
наступним чином:
 ,
,
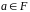 ,
,
отже є полем розкладання многочлена над полем .
На основі представлених лем можна сформулювати головну характеризаційну теорему скінченних полів.
Теорема
(про існування і єдиність скінченних
полів).
Для кожного простого числа
і кожного натурального числа
існує скінченне поле з
елементів.
Будь-яке скінченне поле з
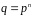 елементів ізоморфне полю розкладання
многочлена
над полем
.
елементів ізоморфне полю розкладання
многочлена
над полем
.
Ця
теорема дозволяє ввести в розгляд, тобто
побудувати конкретне скінченне поле
Галуа порядку
,
що
містить
елементів,
де
–
це степінь простого числа
,
яке є характеристикою цього поля. Поля
цього типу позначають
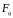 або
або
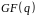 .
.
Позначимо
через
 мультиплікативну групу ненульових
елементів. скінченного поля
.
Наступна теорема встановлює важливу
властивість такої групи.
мультиплікативну групу ненульових
елементів. скінченного поля
.
Наступна теорема встановлює важливу
властивість такої групи.
Теорема.
Мультиплікативна група
поля
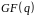 циклічна.
циклічна.
Означення. Твірний елемент циклічної групи називається примітивним елементом поля .
Примітивні елементи скінченного поля за простим розглядалися раніше в теорії чисел під назвою первісних коренів за модулем .
Означення.
Порядком
елемента
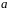 скінченного поля
називається найменше натуральне число
скінченного поля
називається найменше натуральне число
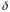 з умовою
з умовою
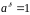 .
Позначається
.
Позначається
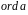 .
.
Якщо – елемент порядку мультиплікативної групи поля , то
 ;
;є дільником числа
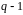 ;
;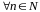
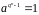 або
або
 .
.
