
- •Лабораторне заняття 2 Тема: Основні алгебраїчні структури
- •1. Бінарні алгебраїчні операції
- •Властивості бінарних алгебраїчних операцій
- •2. Групи
- •3. Кільця
- •4. Поля
- •5. Ізоморфізми та гомоморфізми алгебраїчних структур
- •6. Векторні простори. Алгебри
- •Означення. Лінійною комбінацією векторів векторного простору називається вектор вигляду
- •1. Бінарні алгебраїчні операції
- •2. Групи
- •Групи підстановок
- •4. Кільця і поля
- •5. Ізоморфізми та гомоморфізми алгебраїчних структур
- •6. Векторні простори. Алгебри
2. Групи
Завдання 2.
-
Довести, що множина всіх цілих чисел, які діляться на 3, є абелевою групою відносно операції додавання.
-
Довести, що множина всіх поворотів кола навколо свого центра є групою відносно операції композиції поворотів.
-
Довести, що множина матриць
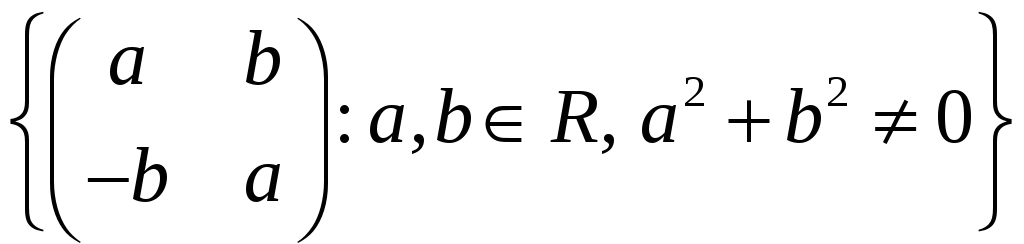 є групою відносно операції множення
матриць.
є групою відносно операції множення
матриць. -
Довести, що множина перетворень
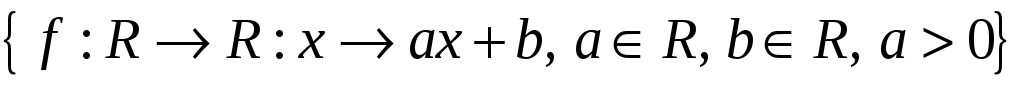 є групою відносно операції композиції
перетворень.
є групою відносно операції композиції
перетворень. -
Довести, що множина матриць
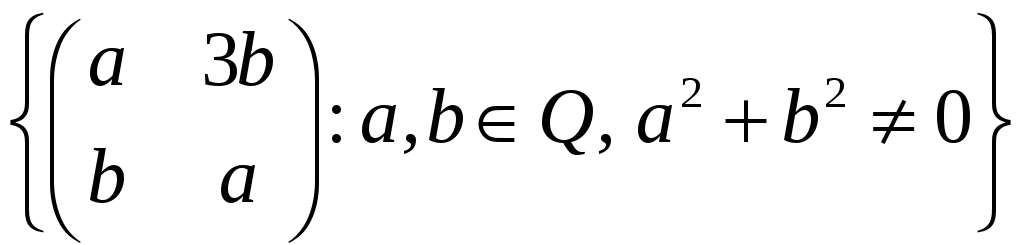 є групою операції відносно множення
матриць.
є групою операції відносно множення
матриць. -
Довести, що множина перетворень
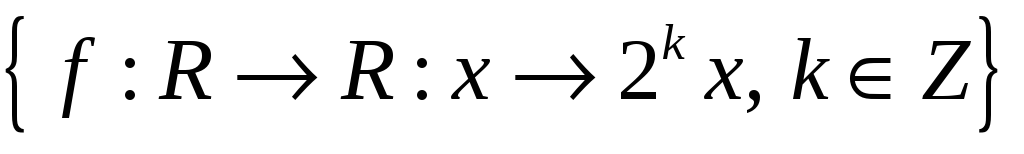 є абелевою групою відносно операції
композиції перетворень.
є абелевою групою відносно операції
композиції перетворень. -
Довести, що множина матриць
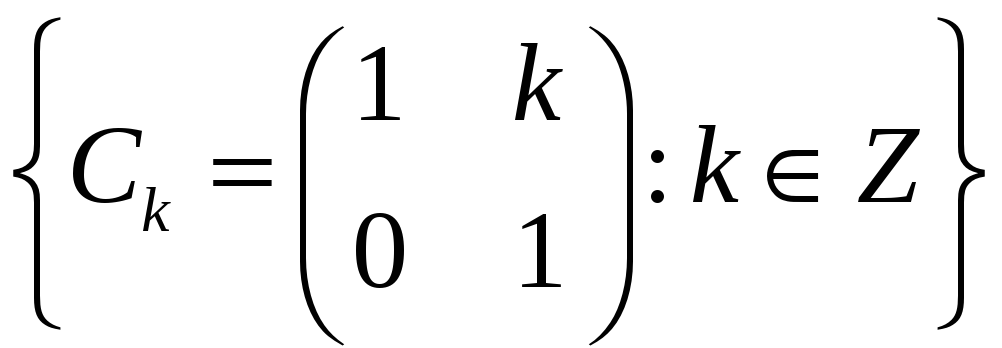 є групою відносно операції множення
матриць.
є групою відносно операції множення
матриць. -
Довести, що множина всіх раціональних чисел, відмінних від 0, є групою відносно операції
 ,
визначеної правилом
,
визначеної правилом
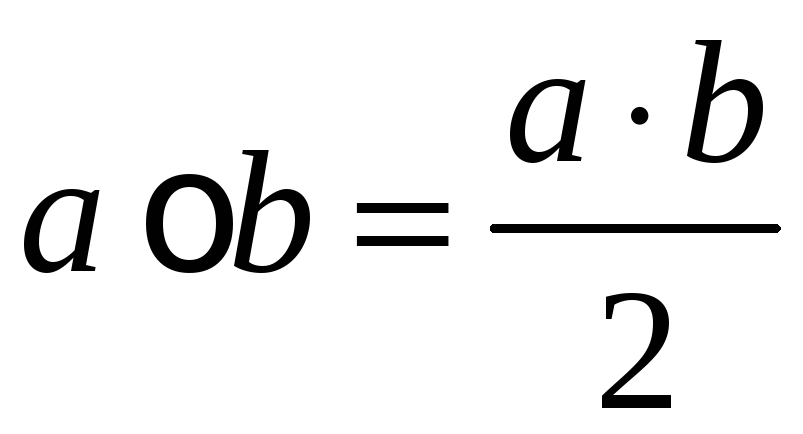 .
. -
Довести, що множина всіх векторів площини є абелевою групою відносно операції додавання векторів.
-
Довести, що множина матриць
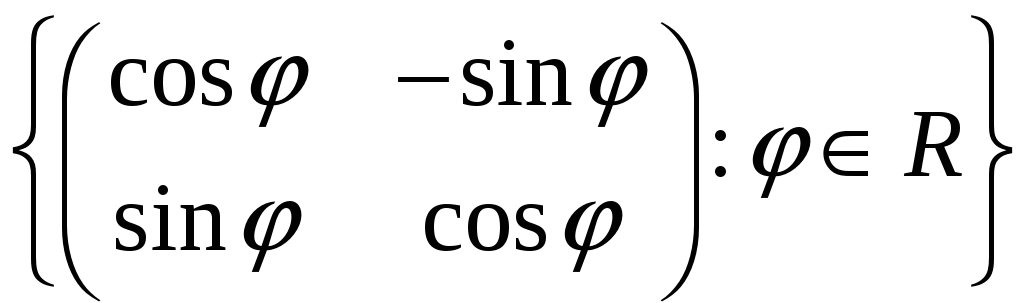 є групою відносно операції множення
матриць.
є групою відносно операції множення
матриць.
Групи підстановок
Завдання 3.
-
Визначити порядки елементів
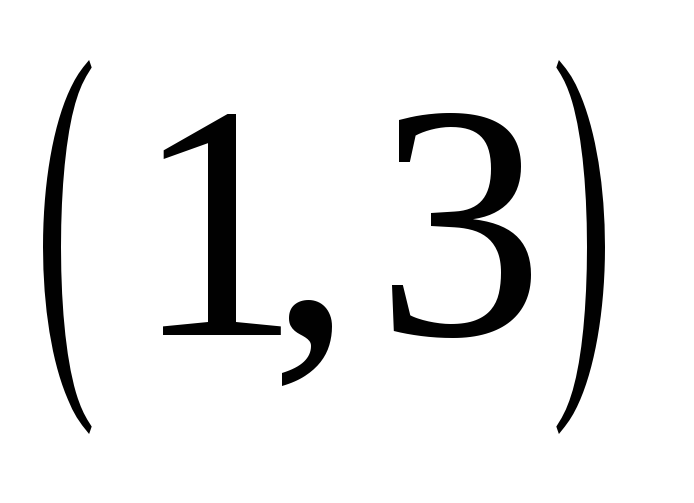 і
і
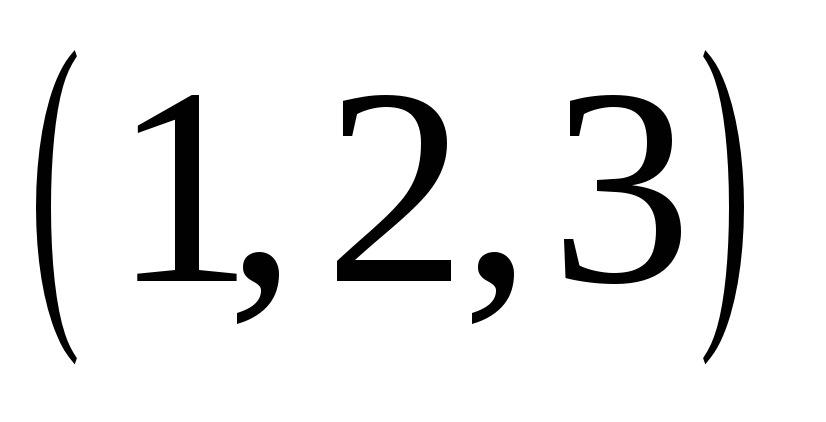 симетричної групи
симетричної групи
 підстановок третього степеня.
підстановок третього степеня. -
Довести, що симетрична група
 підстановок сьомого степеня породжується
множиною
підстановок сьомого степеня породжується
множиною
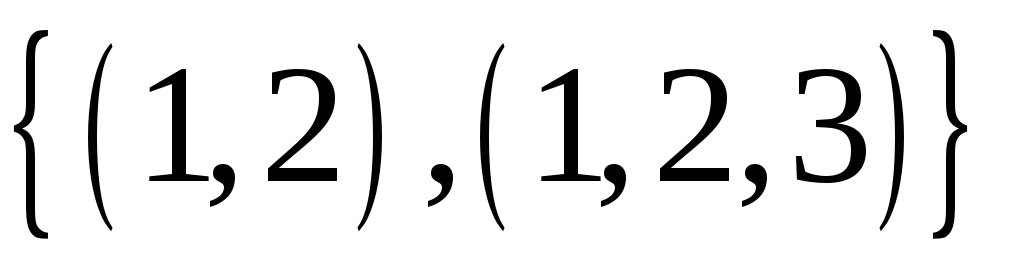 .
. -
В симетричній групі підстановок
 знайти підгрупу
знайти підгрупу
 ,
якщо
,
якщо
 .
. -
Довести, що симетрична група
 підстановок сьомого степеня породжується
множиною
підстановок сьомого степеня породжується
множиною
 .
. -
В симетричній групі підстановок
 знайти добуток елементів
знайти добуток елементів
 і
і
 .
.
-
В симетричній групі підстановок
 знайти підгрупу
знайти підгрупу
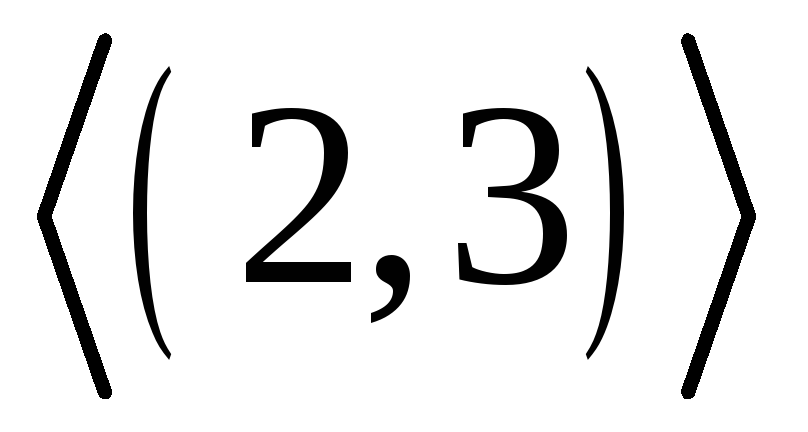 і записати правий суміжний клас за цією
підгрупою.
і записати правий суміжний клас за цією
підгрупою. -
Перевірити, що підгрупа
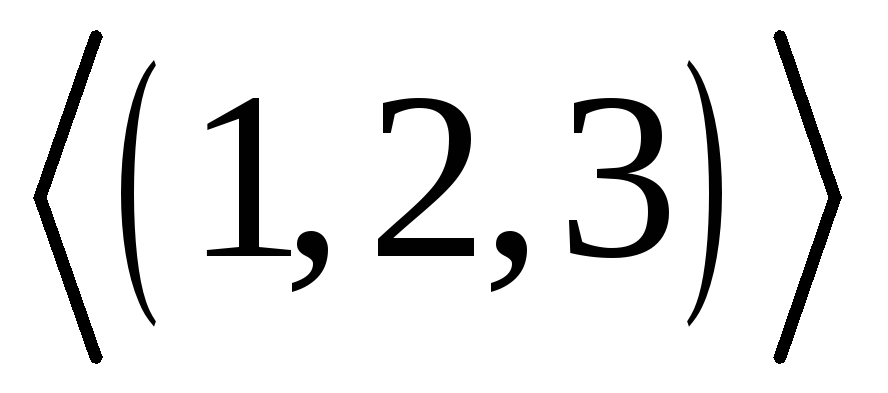 симетричної групи підстановок
симетричної групи підстановок
 є нормальною.
є нормальною. -
В симетричній групі підстановок
 знайти добуток елементів
знайти добуток елементів
 і
і
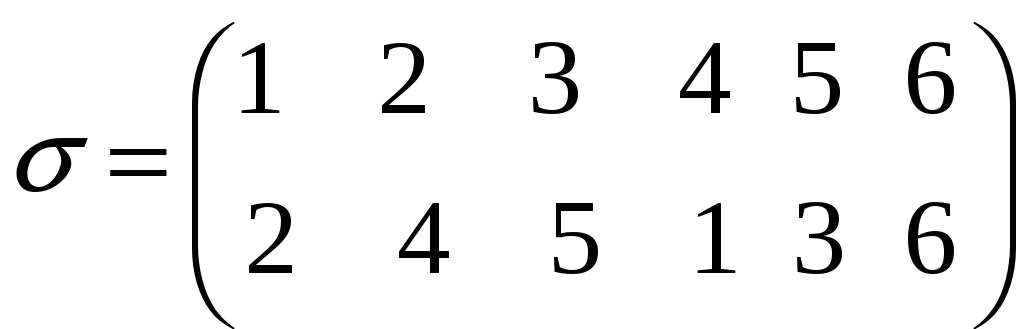 .
.
-
В симетричній групі підстановок
 знайти підгрупу
знайти підгрупу
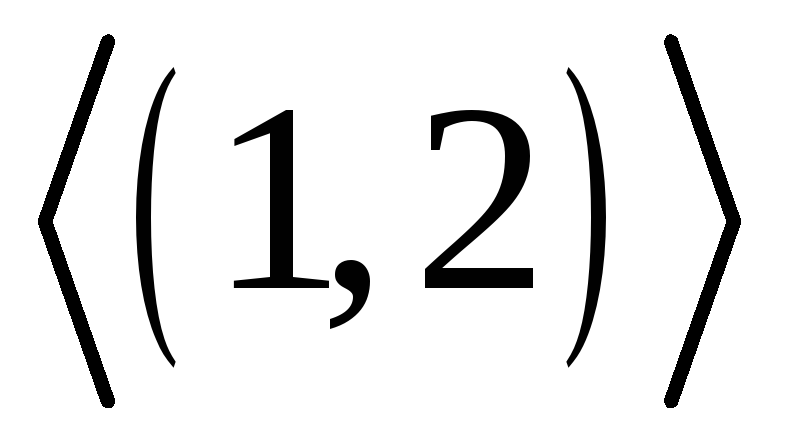 і записати лівий суміжний клас за цією
підгрупою.
і записати лівий суміжний клас за цією
підгрупою. -
В симетричній групі підстановок
 знайти добуток
знайти добуток
 елементів, записаних у вигляді циклів:
елементів, записаних у вигляді циклів:
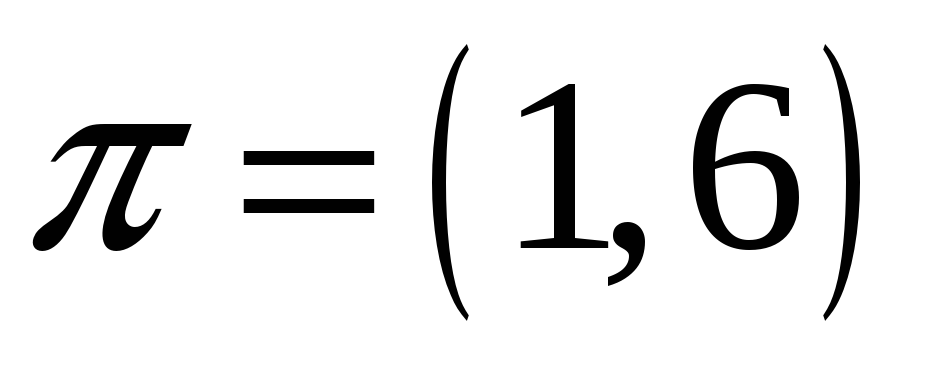 ,
,
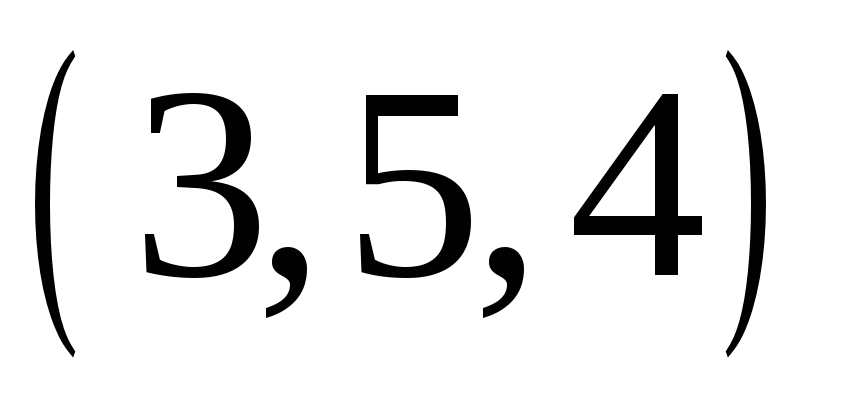 .
. -
Знайти всі підгрупи циклічної групи
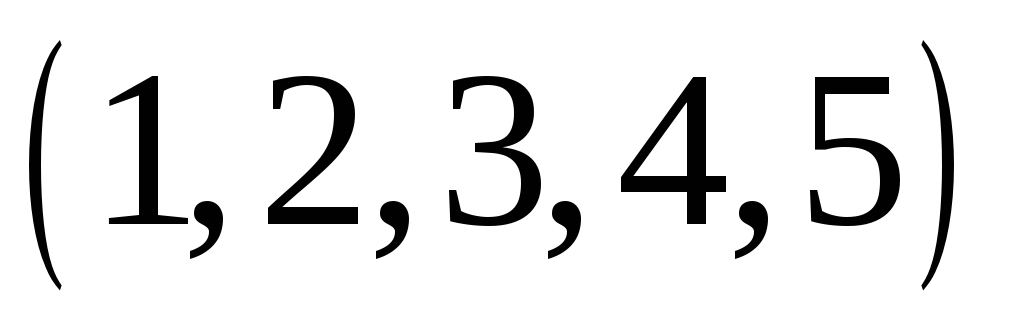 .
.
4. Кільця і поля
Завдання 4.
-
Довести, що множина
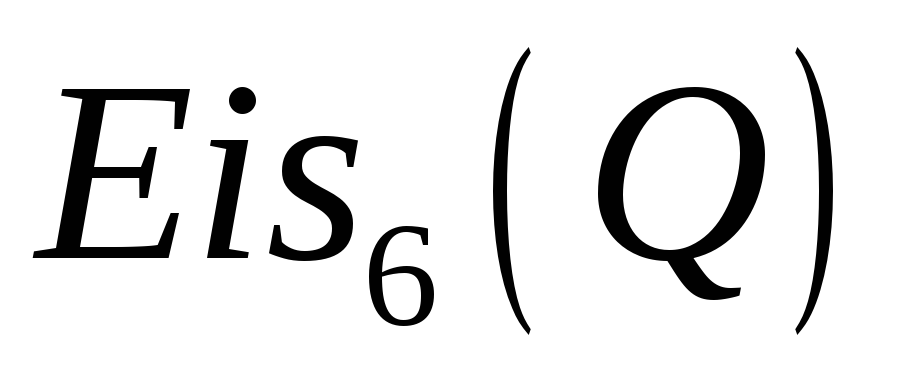 всіх комплексних чисел вигляду
всіх комплексних чисел вигляду
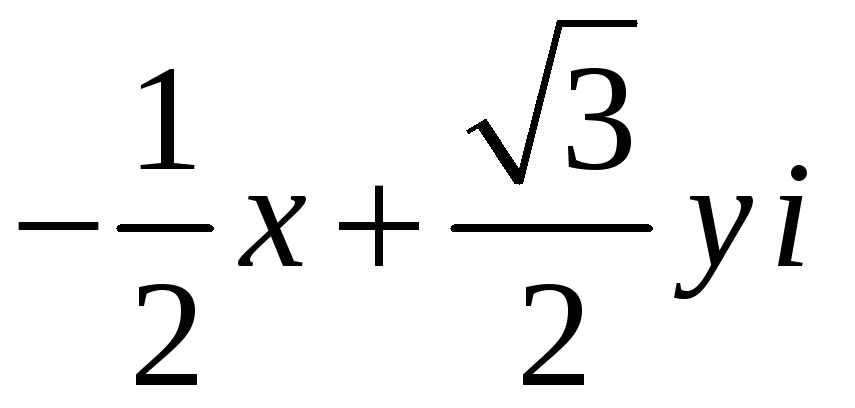 ,
де
,
де
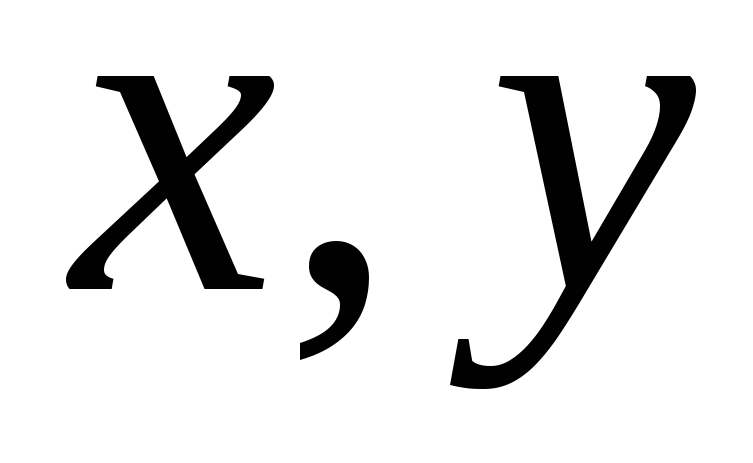 – раціональні числа, є полем.
(Числа такого вигляду називають
раціональними
ейзенштейновими числами.)
– раціональні числа, є полем.
(Числа такого вигляду називають
раціональними
ейзенштейновими числами.) -
Довести, що множина
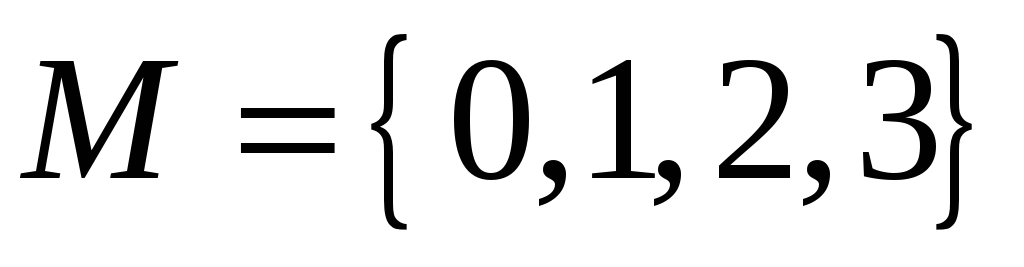 з операціями + і
з операціями + і
 , заданими таблицями Келі:
, заданими таблицями Келі:
|
+ |
0 |
1 |
2 |
3 |
|
0 |
0 |
1 |
2 |
3 |
|
1 |
1 |
2 |
3 |
0 |
|
2 |
2 |
3 |
0 |
1 |
|
3 |
3 |
0 |
1 |
2 |
|
. |
0 |
1 |
2 |
3 |
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
2 |
3 |
|
2 |
0 |
2 |
0 |
0 |
|
3 |
0 |
3 |
0 |
1 |
є комутативним кільцем з одиницею.
-
Довести, що множина 2х2-матриць вигляду
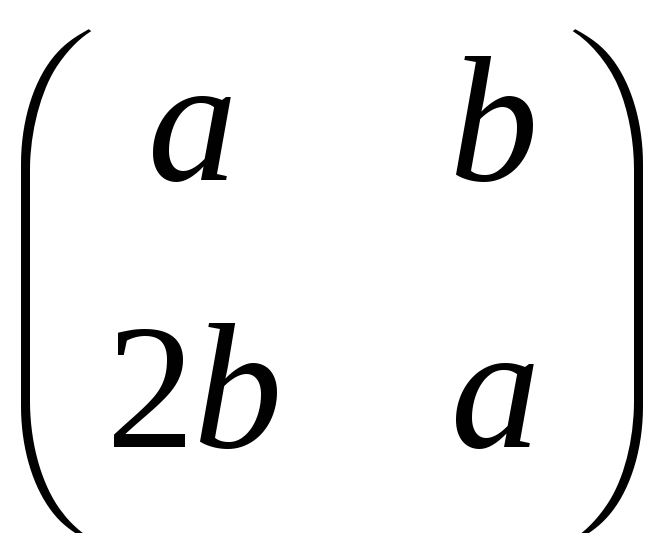 ,
де
,
де
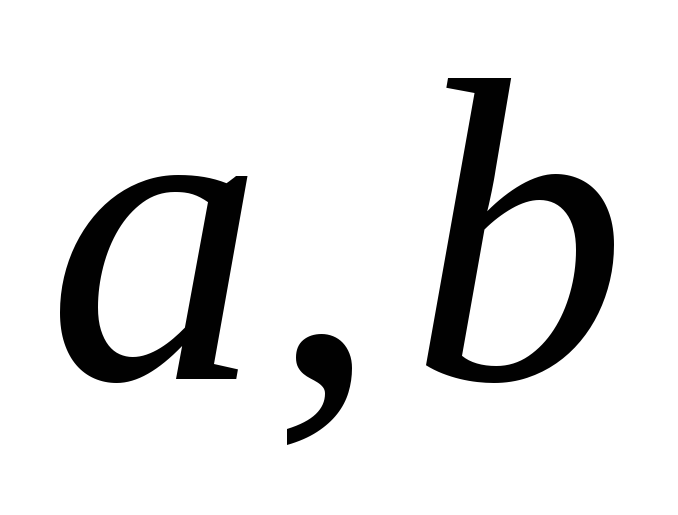 – раціональні числа,
є полем.
– раціональні числа,
є полем. -
Довести, що множина
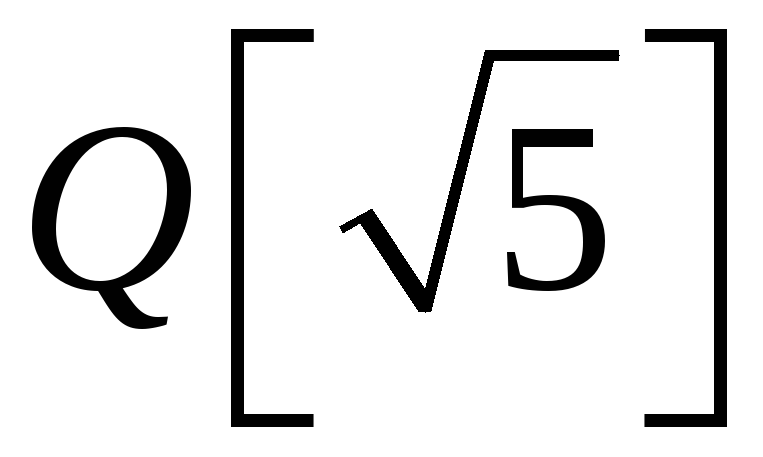 всіх дійсних чисел вигляду
всіх дійсних чисел вигляду
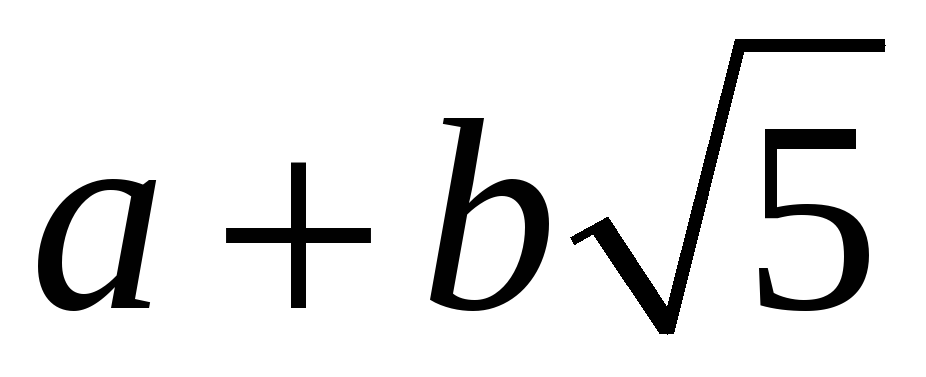 ,
де
,
де
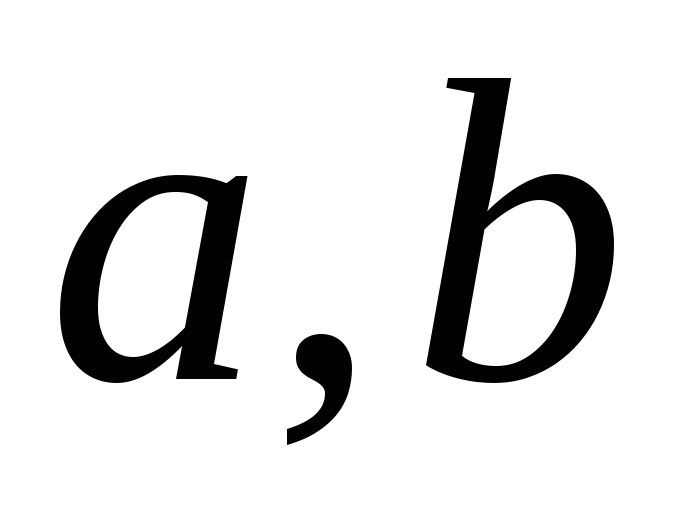 – цілі числа, є комутативним
кільцем з одиницею.
– цілі числа, є комутативним
кільцем з одиницею. -
Довести, що множина всіх цілих чисел виду
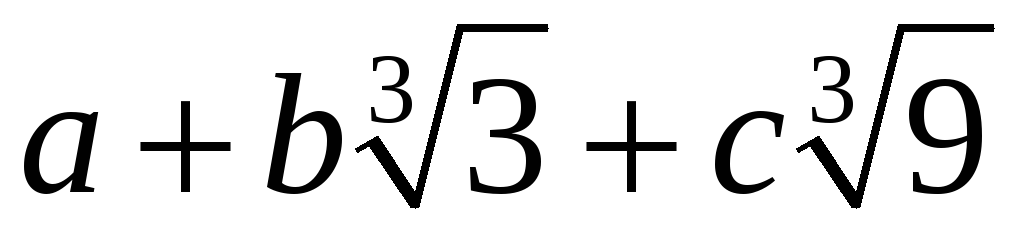 ,
де
,
де
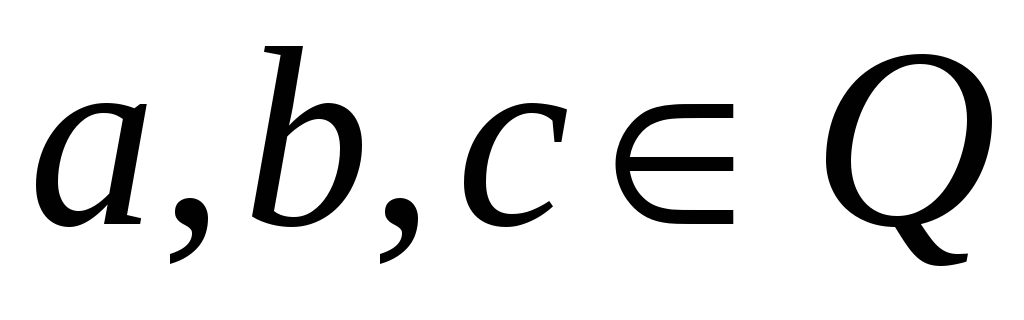 ,
є полем.
,
є полем. -
Довести, що множина всіх комплексних чисел вигляду
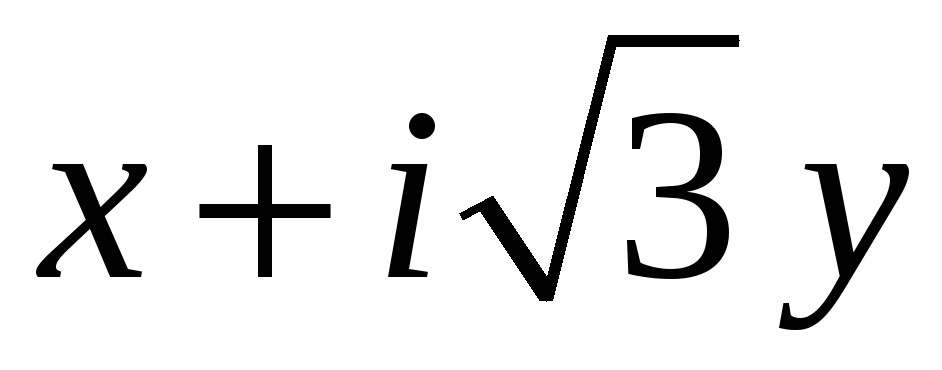 ,
де
,
де
 – раціональні, є комутативним
кільцем з одиницею.
– раціональні, є комутативним
кільцем з одиницею. -
Довести, що множина
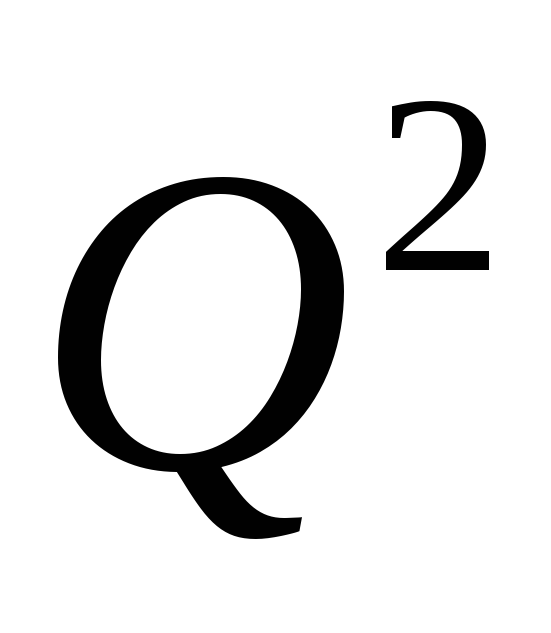 з операціями, визначеними рівностями:
з операціями, визначеними рівностями:
![]() ,
,
![]() ,
,
є полем. Яку характеристику має це поле?
-
Довести, що множина 2х2-матриць вигляду
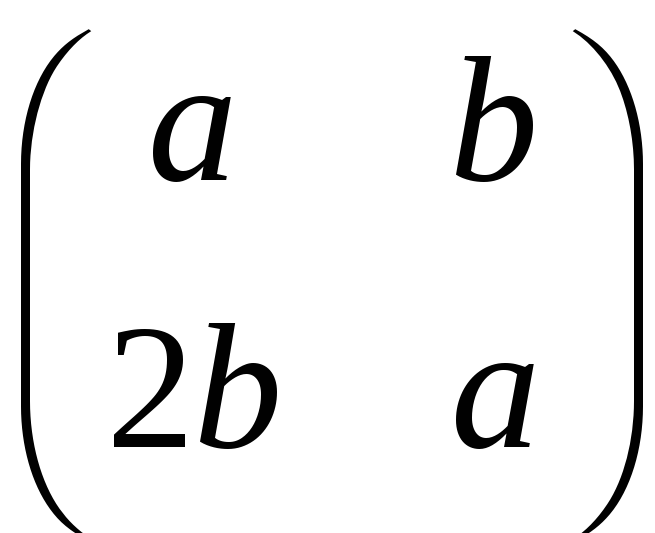 ,
де
,
де
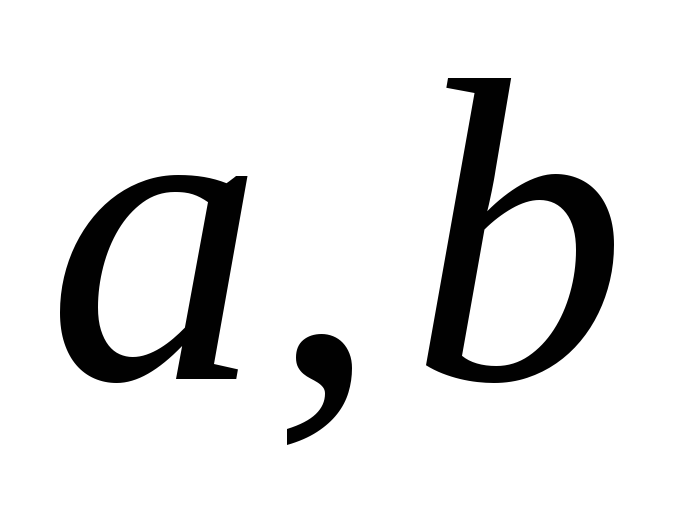 – дійсні числа,
є кільцем відносно звичайних операцій
додавання і множення
матриць.
– дійсні числа,
є кільцем відносно звичайних операцій
додавання і множення
матриць. -
Довести, що множина
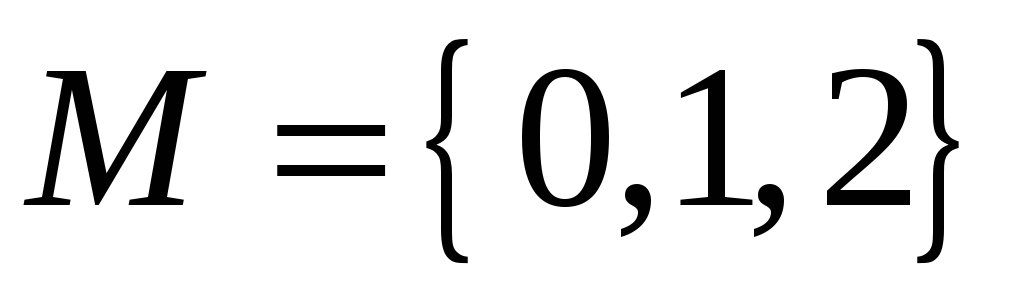 з операціями + і
з операціями + і
 , заданими таблицями Келі:
, заданими таблицями Келі:
|
+ |
0 |
1 |
2 |
|
0 |
0 |
1 |
2 |
|
1 |
1 |
2 |
0 |
|
2 |
2 |
0 |
1 |
|
. |
0 |
1 |
2 |
|
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
2 |
|
2 |
0 |
2 |
1 |
є полем. Яку характеристику має це поле?
-
Довести, що множина 2х2-матриць
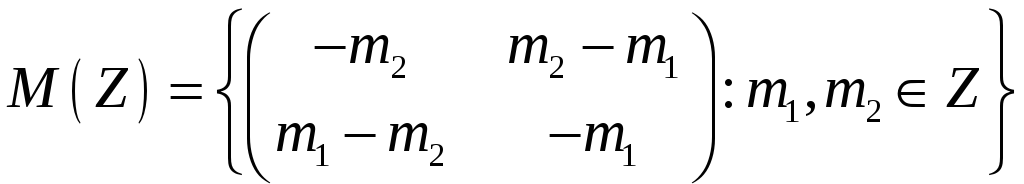 є
комутативним
кільцем.
є
комутативним
кільцем.
