1. Бінарні алгебраїчні операції

Завдання 1.

1. На множині задані дві бінарні операції: додавання + і множення . Показати, що:

а) обидві операції комутативні;

б) в множині не існує елемент (число) такий, що ;

в) в множині не існує нейтрального елемента відносно операції +;

г) в множині існує елемент (число) такий, що для будь-якого . Вкажіть цей елемент.

д) операції, обернені до додавання + і множення визначені частково.

2. Операція на множині задана таблицею:

	a	b	c	d
a	a	a	a	a
b	b	b	b	b
c	c	c	c	c
d	d	d	d	d

Довести, що операція асоціативна і некомутативна. Чи існує нейтральний елемент відносно операції ?

3. На множині натуральних чисел визначена алгебраїчна операція рівністю:

.

З'ясувати:

1. які властивості має ця операція.

2. чи існують елементи, виділені відносно цієї операції?

4. На множині чисел визначені операції ,,додавання‘‘ і ,,множення‘‘ наступними таблицями:

	0	1	–1
0	0	1	–1
1	1	–1	0
–1	–1	0	1

	0	1	–1
0	0	0	0
1	0	1	–1
–1	0	–1	1

Нехай 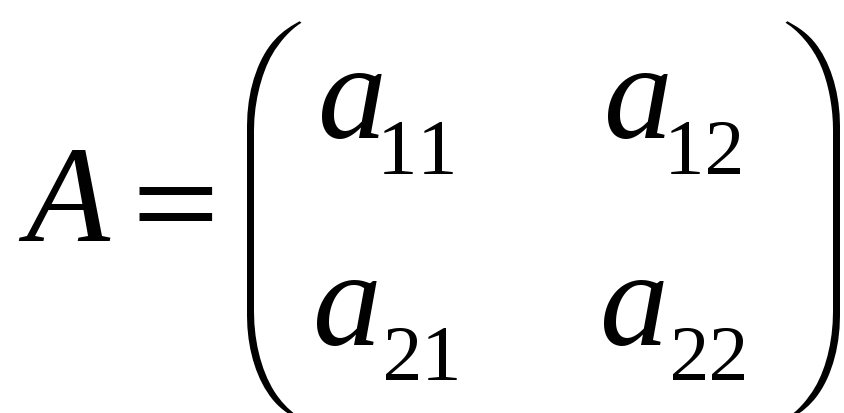і 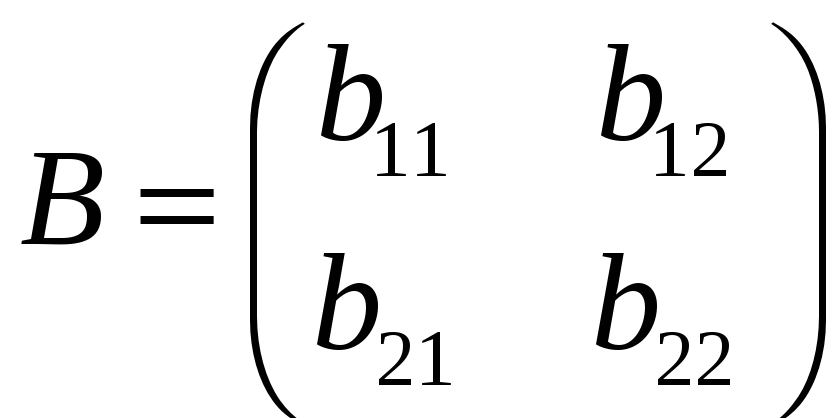– -матриці з елементами з множини . Будемо додавати і множити матриці і , замінюючи додавання + на і множення на . Обчислити , , , ,, , якщо

, , .

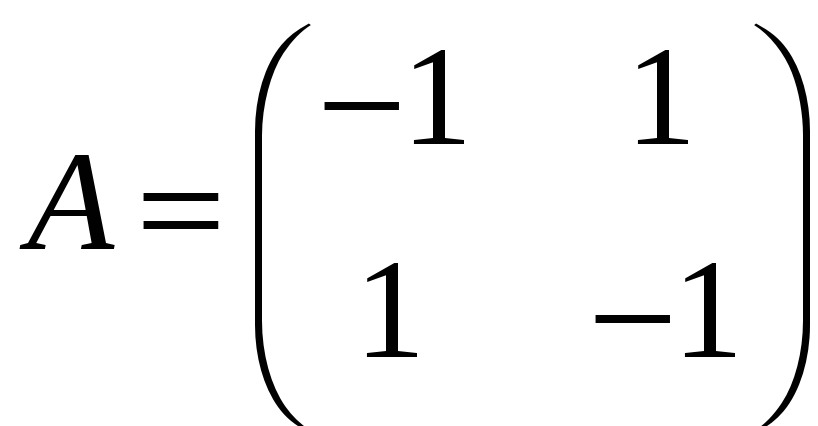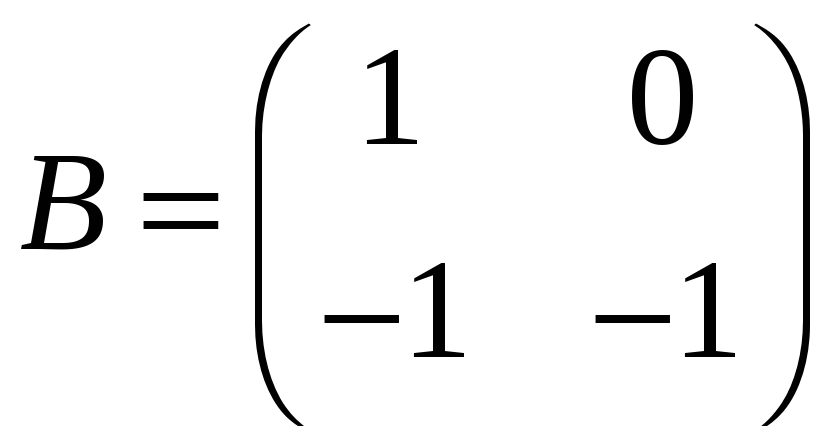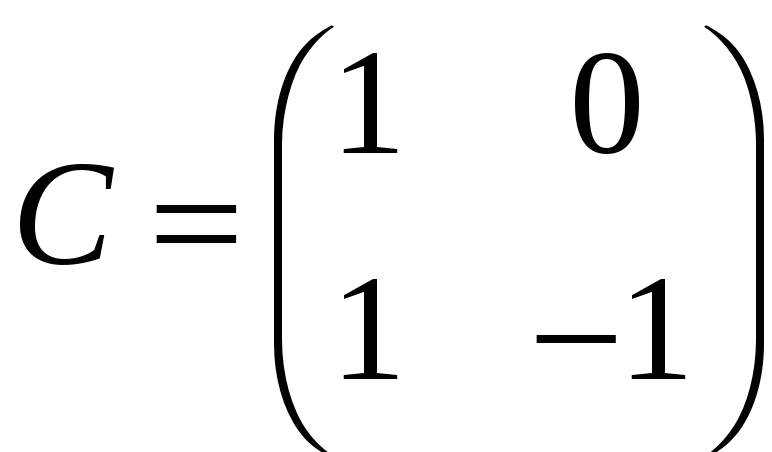5. На множині визначені операції:

;

,

Довести, що операція множення комутативна, асоціативна і дистрибутивна відносно операції додавання.

6. У множині задано бінарну операцію так, що є остачею від ділення суми на число 6.

а) Задати бінарну операцію таблицею Келі;

б) Визначити властивості операції ;

в) Визначити елементи, виділені відносно операції .

7. На множині пар дійсних чисел визначена операція множення * наступним правилом:

для будь-яких пар ,

.

Позначимо , . Тоді . Скласти таблицю Келі для операції * . З'ясувати:

1. які властивості має ця операція.

2. чи існують елементи, виділені відносно цієї операції?

8. На множині натуральних чисел визначена алгебраїчна операція рівністю:

,

де – НСК чисел .

З'ясувати:

1. які властивості має ця операція.

2. чи існують елементи, виділені відносно цієї операції?

9. На множині визначені операції:

;

,

Довести, що операція множення комутативна, асоціативна і дистрибутивна відносно операції додавання.

10. На множині дійсних чисел визначена алгебраїчна операція рівністю:

.

З'ясувати:

3. які властивості має ця операція.

4. чи існують елементи, виділені відносно цієї операції?