21

Лабораторне заняття 2 Тема: Основні алгебраїчні структури

Мета заняття: 1. Закріпити лекційний матеріал з основних алгебраїчних структур.

2. Навчитися визначати тип і властивості алгебраїчної структури, яку задають бінарні алгебраїчні операції на певній множині.

І. Короткі теоретичні відомості.(див. лекції 2)

1. Бінарні алгебраїчні операції

Означення. Нехай – довільна множина елементів . Бінарною алгебраїчною операцією (або законом композиції) на множині називається довільне (але фіксоване) відображення декартового квадрата в . Таким чином, будь-якій впорядкованій парі елементів однозначно ставиться у відповідність певний третій елемент тієї ж множини .

Іноді замість пишуть , а ще частіше конкретну бінарну операцію позначають спеціальним символом: +, •, &, , , і т.д.

Звичайно бінарна операція на скінченній множині з елементів задається так званою таблицею Келі, яка являє собою квадратну -таблицю з двома входами, кожній клітинці якої відповідає впорядкована пара елементів даної множини, елемент стоїть у вибраному рядку, елемент – у вибраному стовпці.

Властивості бінарних алгебраїчних операцій

Комутативність: .

Асоціативність: :.

Дистрибутивність зліва:

Дистрибутивність справа:

Якщо для будь-яких двох елементів і множини існує в множині одна і тільки одна пара елементів і таких, що і , то кажуть, що для визначеної на множині бінарної алгебраїчної операції виконується обернена операція, яку позначають .

Означення. Якщо існує елемент такий, що , то він називається ідемпотентним по відношенню до операції , або просто ідемпотентом.

Означення. Якщо існує елемент такий, що

то він називається нейтральним відносно операції , або одиничним.

Теорема (про єдиність нейтрального елемента). Якщо відносно операції існує нейтральний елемент, то він єдиний.

Означення. Елемент називається симетричним елементу відносно операції , якщо

,

де – нейтральний відносно операції елемент.

Теорема (про єдиність симетричного елемента). Якщо бінарна операція , визначена на множині , асоціативна, то для будь-якого елемента в ньому може існувати не більше одного симетричного елемента.

2. Групи

Означення. Непорожня множина , на якій визначена бінарна алгебраїчна операція , називається групою, якщо виконуються наступні умови (аксіоми групи):

1. операція асоціативна: ;

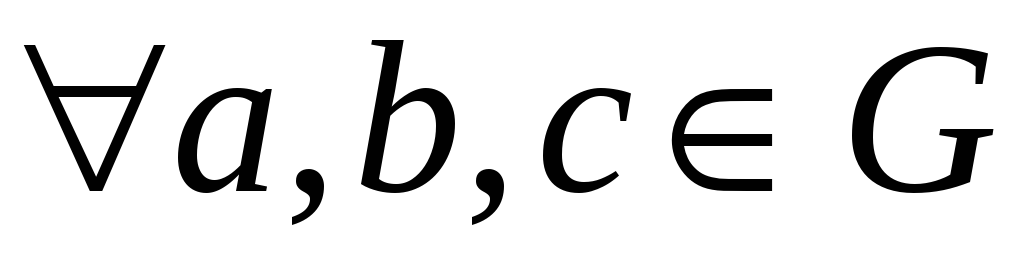
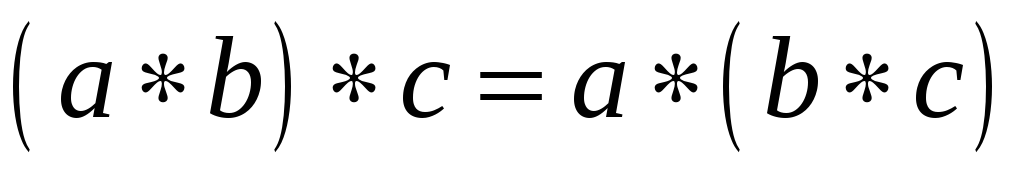2. в множині існує нейтральний елемент ; ;

3. для кожного елемента 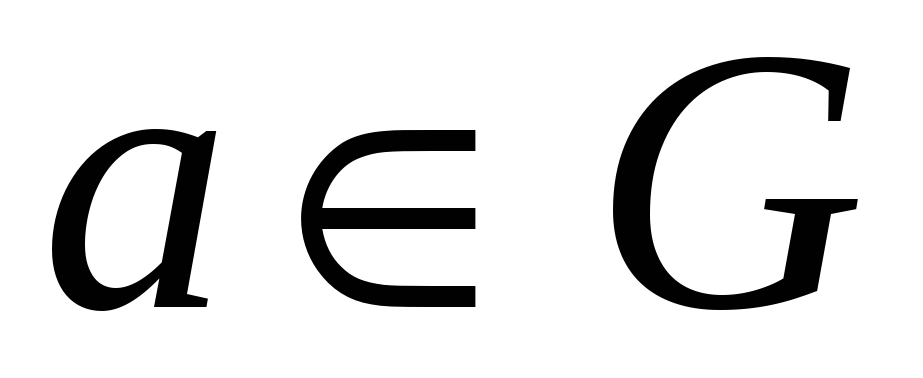існує симетричний елемент : .

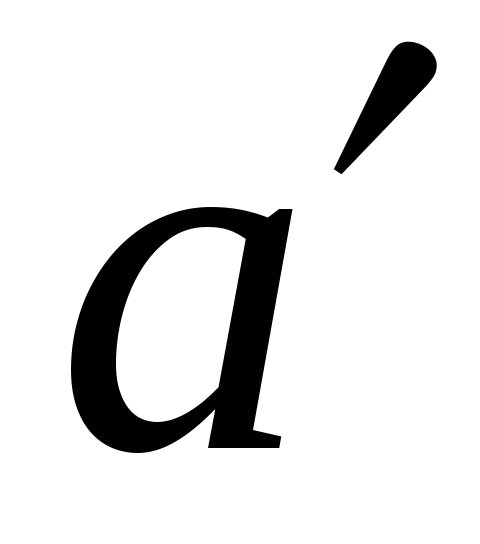Якщо

4) операція комутативна: ,

група називається абелевою.

Якщо задану на групі операцію називають множенням, то використовують мультиплікативну форму запису, саму групу при цьому називають мультиплікативною або групою по множенню. Якщо ж задану на групі операцію називають додаванням, то використовують адитивну форму запису, саму групу при цьому називають адитивною або групою по додаванню.

Означення. Підмножина називається підгрупою групи , якщо є групою відносно бінарної алгебраїчної операції , заданої на групі .( позначається: ).

Теорема (критерій підгрупи). Для того, щоб непорожня підмножина групи була б підгрупою групи , необхідно і достатньо, щоб підмножина :

1. разом з будь-якими своїми елементами і містила б також їх композицію ;

2. разом з будь-яким своїм елементом містила б також і симетричний елемент .

Означення. Нехай – підгрупа групи . Лівим суміжним класом групи (або лівим класом суміжності) по підгрупі називається множина елементів вигляду , де – фіксований елемент з , а перебігає всі елементи підгрупи :

, .

Елемент називається представником суміжного класу .

Теорема (про розклад групи на ліві суміжні класи по підгрупі ). Два лівих суміжні класи групи по підгрупі збігаються або не мають спільних елементів. Розбиття на ліві суміжні класи по

визначає на відношення еквівалентності.

Означення. Група, в якій всі елементи основної множини є степенями одного елемента , тобто є результатами k-кратного застосування операції (k=0,1,2,...), називається циклічною. Цей єдиний елемент називається твірним елементом циклічної групи. Циклічна група з твірним елементом позначається так: .

Циклічна група з твірним елементом є абелевою групою вигляду або в залежності від того, яка група розглядається – мультиплікативна або адитивна.

Теорема (про порядок елемента групи). Порядок будь-якого елемента довільної групи дорівнює порядку породженої ним циклічної групи:

.

Якщо – елемент скінченного порядку , то

і .

Означення. Група, елементами якої є всі взаємно однозначні відображення скінченної множини з елементів самої в себе, називається симетричною групою -го степеня (позначається через ).

Елементи симетричної групи називаються підстановками. Тому і групу також називають ще групою підстановок.

У розгорненій і наочній формі підстановку , , зображають дворядним символом:

,

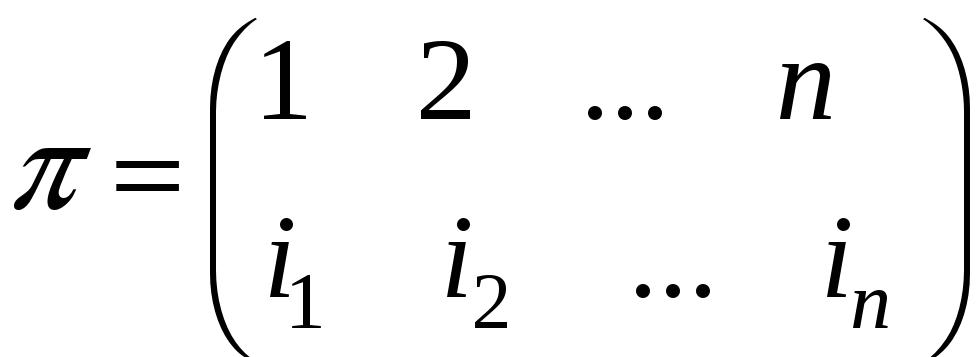Порядок групи підстановок дорівнює числу перестановок з елементів, тобто :

.

Означення. Циклічною перестановкою або просто циклом називається підстановка така, що при повторенні її достатню кількість разів будь-який з символів, що дійсно переміщується, може бути переведений в будь-який інший з таких символів.

Означення. Довжиною циклу називається число символів, яке дійсно переміщується циклом.

Розклад на цикли є зручним способом запису підстановок.

Приклад.

.

Означення. Цикл довжини 2 називається транспозицією.

Теорема. Будь-яка перестановка є добутком транспозицій. Цей розклад визначений однозначно з точністю до порядку слідування циклів.

Теорема Лагранжа. Порядок скінченої групи ділиться на порядок кожної своєї підгрупи:

.

Означення. Підгрупа групи називається нормальним дільником цієї групи (або інваріантною підгрупою), якщо

1. лівосторонній розклад групи по підгрупі збігається з правостороннім.

або

2. для будь-якого елемента .

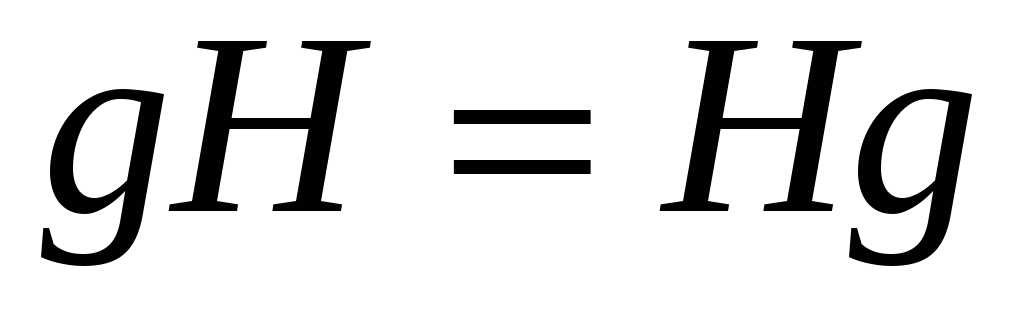(позначається так: ).

Значення нормального дільника засновано на тому, що з суміжних класів по нормальному дільнику деяким природним способом може бути побудована нова група.

Теорема (про факторгрупу). Якщо – нормальний дільник групи , то операція множення наділяє множину суміжних класів по структурою групи, яка називається факторгрупою по . Суміжний клас є одиничним елементом факторгрупи, а – елементом, оберненим до .

(Позначається .)