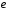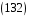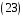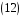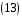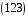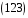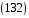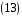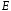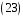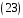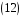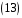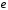- •Виконав(ла): студент(ка) бсдм(с)(убдм(с)) – 51
- •Властивості бінарних алгебраїчних операцій
- •2. Групи
- •3. Кільця
- •4. Поля
- •5. Ізоморфізми та гомоморфізми алгебраїчних структур
- •6. Векторні простори. Алгебри
- •Означення. Лінійною комбінацією векторів векторного простору називається вектор вигляду
- •1. Бінарні алгебраїчні операції
- •2. Групи
- •Симетрична і знакозмінна групи
- •3,4. Кільця і поля
- •5. Ізоморфізми та гомоморфізми алгебраїчних структур
- •6. Векторні простори. Алгебри
Симетрична і знакозмінна групи
Завдання
2.
В
симетричній групі підстановок
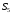 знайти добуток
знайти добуток
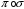 елементів, записаних у вигляді циклів:
елементів, записаних у вигляді циклів:
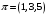 ,
,
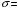
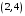 .
.
Розв'язання.
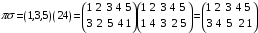 .
.
3,4. Кільця і поля
Завдання 3.
1.
Довести, що множина
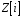 всіх чисел виду
всіх чисел виду
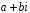 ,
де
,
де
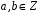 ,
,
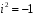 ,
є кільцем відносно звичайних операцій
додавання і множення.
,
є кільцем відносно звичайних операцій
додавання і множення.
Доведення.
Нехай
 і
і
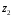 – два довільних елементи з множини
– два довільних елементи з множини
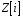 .
Тоді
.
Тоді
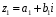 ,
,
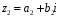 ,
де
,
де
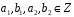 .
Маємо:
.
Маємо:
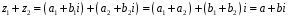 ,
,
де
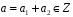 ,
,
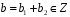 .
.
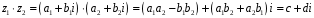 ,
,
де
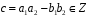 ,
,
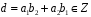 .
.
Оскільки
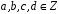 ,
то
,
то
 і
і
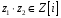 ,
тобто додавання
і множення
є алгебраїчними операціями на множині
,
тобто додавання
і множення
є алгебраїчними операціями на множині
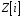 .
.
Аксіоми
асоціативності, комутативності операцій
додавання
і множення,
дистрибутивності множення
відносно додавання
виконуються на множині
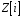 ,
оскільки виконуються
для будь-яких комплексних чисел.
,
оскільки виконуються
для будь-яких комплексних чисел.
Нульовий
елемент
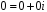 і одиничний елемент
і одиничний елемент
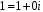 належать, очевидно, множині
належать, очевидно, множині
 .
.
Якщо
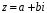 – довільне число з
– довільне число з
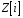 ,
то протилежне до нього число
,
то протилежне до нього число
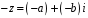 належить множині
належить множині
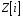 .
.
Таким
чином,
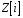 – комутативне кільце з одиницею. Його
називають кільцем цілих гауссових
чисел.
– комутативне кільце з одиницею. Його
називають кільцем цілих гауссових
чисел.
2.
Довести, що
множина
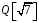 чисел вигляду
чисел вигляду
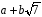 ,
де
,
де
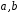 – раціональні числа, є полем.
– раціональні числа, є полем.
Доведення.
Доведемо
спочатку, що множина
 є кільцем.
є кільцем.
Оскільки
множина
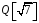 є підмножиною кільця
є підмножиною кільця
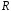 дійсних чисел, то можна скористатися
критерієм підкільця.
дійсних чисел, то можна скористатися
критерієм підкільця.
Нехай
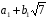 ,
,
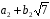 – два довільні елементи із
– два довільні елементи із
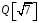 .
Тоді
.
Тоді
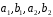 – раціональні числа, і отже,
– раціональні числа, і отже,
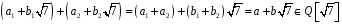 ,
,
оскільки
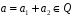 ,
,
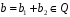 ;
;
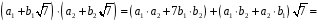
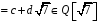 ,
,
оскільки
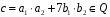 ,
,
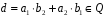 ;
;
 ,
,
оскільки
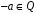 ,
,
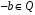 .
.
В
силу критерію підкільця,
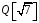 – підкільце кільця
– підкільце кільця
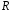 ,
а отже, кільце.
,
а отже, кільце.
Оскільки
 ,
то
,
то
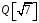 – комутативне кільце з одиницею.
– комутативне кільце з одиницею.
Нехай
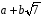 – довільний ненульовий елемент з
– довільний ненульовий елемент з
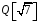 ,
тобто такий, що
,
тобто такий, що
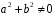 ,
і нехай
,
і нехай
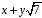 – такий елемент з
– такий елемент з
 ,
що
,
що
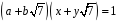 . (1)
. (1)
Покажемо,
що
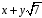 міститься в
міститься в
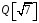 .
Виконавши операцію множення в лівій
частині рівності (1), отримуємо:
.
Виконавши операцію множення в лівій
частині рівності (1), отримуємо:
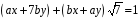 ,
,
звідси
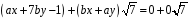 .
.
Отримана рівність еквівалентна системі лінійних алгебраїчних рівнянь:

Розв’язавши дану систему, будемо мати:
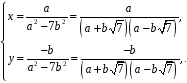
Оскільки
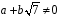 ,
то і
,
то і
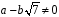 ,
значить,
,
значить,
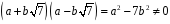 .
.
Отже,
числа
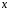 і
і
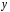 за даними числами
за даними числами
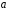 і
і
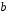 завжди можна визначити, причому
завжди можна визначити, причому
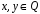 .
Значить,
.
Значить,
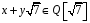 .
Таким чином, для кожного ненульового
елемента
.
Таким чином, для кожного ненульового
елемента
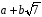 із
із
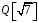 завжди існує в
завжди існує в
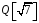 обернений до нього елемент:
обернений до нього елемент:
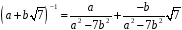 .
.
Отже,
множина
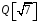 чисел вигляду
чисел вигляду
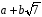 ,
де
,
де
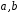 – раціональні числа, є полем.
– раціональні числа, є полем.
5. Ізоморфізми та гомоморфізми алгебраїчних структур
Завдання 4.
1.
Довести,
що адитивна група
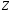 ізоморфна мультиплікативній групі всіх
цілих степенів числа 2.
ізоморфна мультиплікативній групі всіх
цілих степенів числа 2.
Доведення.
Щоб довести, що групи
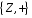 і
і
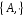 ,
де
,
де
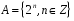 ,
ізоморфні, треба вказати хоча б один
ізоморфізм
,
ізоморфні, треба вказати хоча б один
ізоморфізм
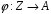 .
.
Зіставимо
кожному
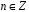
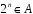 .
Тоді
.
Тоді
 .
.
Перевіримо,
що
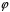 – ізоморфізм.
– ізоморфізм.
1)
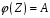 –
–
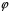 сюр‘єкція
сюр‘єкція
2)
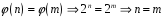 –
–
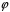 ін‘єкція
ін‘єкція
Отже,
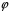 – бієкція.
– бієкція.
Перевіримо,
що
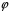 зберігає групову операцію, тобто
зберігає групову операцію, тобто
 .
.
Дійсно,
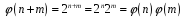 .
.
Таким
чином, відображення
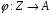 таке, що
таке, що
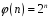 є ізоморфізмом груп.
є ізоморфізмом груп.
2.
Довести,
що група
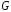 всіх симетрій правильного трикутника
()див. завдання 1) ізоморфна симетричній
групі
всіх симетрій правильного трикутника
()див. завдання 1) ізоморфна симетричній
групі
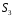 .
.
Доведення. Всім шести перетворенням симетрії відповідають перестановки на множині вершин трикутника.
Нехай
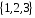 – множина вершин
трикутника,
– множина вершин
трикутника,
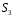 – симетрична група 3-го степеня.
– симетрична група 3-го степеня.
Складемо
таблицю Келі для групи
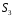 :
:
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Бачимо,
що таблиці Келі для групи
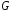 всіх
симетрій правильного трикутника
і симетричної
групі
всіх
симетрій правильного трикутника
і симетричної
групі
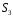 мають однакову структуру.
Це означає, що відображення:
мають однакову структуру.
Це означає, що відображення:
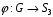 :
:
 ,
,
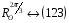 ,
,
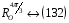 ,
,
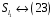 ,
,
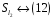 ,
,
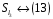
є ізоморфізмом груп.
Таким
чином,
 .
.
3.
Довести,
що кільце
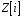 цілих гауссових чисел ізоморфне кільцю
цілих гауссових чисел ізоморфне кільцю
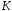 матриць вигляду
матриць вигляду
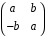 ,
де
,
де
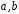 – цілі числа.
– цілі числа.
Доведення.
Поставимо у відповідність елементу
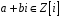 матрицю
матрицю
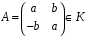
Цим
задане відображення
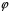 кільця
кільця
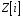 на кільце
на кільце
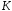 .
Покажемо, що
.
Покажемо, що
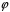 є взаємно однозначним відображенням
є взаємно однозначним відображенням
 кільця
кільця
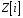 на кільце
на кільце
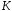 .
.
Нехай
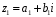 ,
,
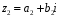 – довільні два елементи із
– довільні два елементи із
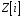 такі, що
такі, що
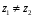 .
тоді або
.
тоді або
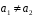 ,
або
,
або
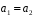 і
і
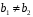 .
Отже,
.
Отже,
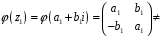
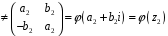
Покажемо,
що
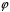 зберігає операції додавання і множення.
Нехай
зберігає операції додавання і множення.
Нехай
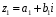 ,
,
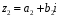 – довільні два елементи із
– довільні два елементи із
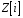 .
Тоді:
.
Тоді:
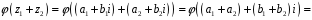
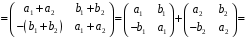
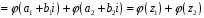 ;
;
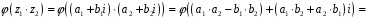
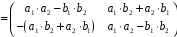 ;
;
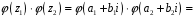
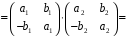
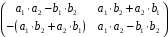 .
.
З
останніх двох рівностей випливає, що
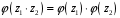 .
Таким чином,
.
Таким чином,
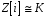 .
.
4.
Довести, що
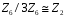 .
.
Доведення.
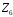 – кільце класів лишків за модулем 6.
Складемо таблиці Келі для операцій
кільця
– кільце класів лишків за модулем 6.
Складемо таблиці Келі для операцій
кільця
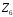 :
:
|
+ |
0 |
1 |
2 |
3 |
4 |
5 |
|
0 |
0 |
1 |
2 |
3 |
4 |
5 |
|
1 |
1 |
2 |
3 |
4 |
5 |
0 |
|
2 |
2 |
3 |
4 |
5 |
0 |
1 |
|
3 |
3 |
4 |
5 |
0 |
1 |
2 |
|
4 |
4 |
5 |
0 |
1 |
2 |
3 |
|
5 |
5 |
0 |
1 |
2 |
3 |
4 |
|
. |
0 |
1 |
2 |
3 |
4 |
5 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
2 |
0 |
2 |
4 |
0 |
2 |
4 |
|
3 |
0 |
3 |
0 |
3 |
0 |
3 |
|
4 |
0 |
4 |
2 |
0 |
4 |
2 |
|
5 |
0 |
5 |
4 |
3 |
2 |
1 |
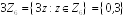 – головний
ідеал кільця
– головний
ідеал кільця
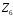 .
.
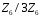 – факторкільце
кільця
– факторкільце
кільця
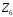 за ідеалом
за ідеалом
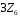 .
Складемо
таблицю Келі для операцій кільця
.
Складемо
таблицю Келі для операцій кільця
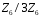 :
:
|
. |
0 |
3 |
|
0 |
0 |
0 |
|
3 |
0 |
3 |
|
+ |
0 |
3 |
|
0 |
0 |
3 |
|
3 |
3 |
0 |
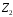 – кільце
класів лишків за модулем 2. Складемо
таблиці Келі для операцій кільця
– кільце
класів лишків за модулем 2. Складемо
таблиці Келі для операцій кільця
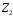 :
:
|
. |
0 |
1 |
|
0 |
0 |
0 |
|
1 |
0 |
1 |
|
+ |
0 |
1 |
|
0 |
0 |
1 |
|
1 |
1 |
0 |
Бачимо,
що таблиці Келі для кільця
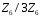 і кільця
і кільця
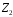 мають однакову структуру.
Це означає, що відображення:
мають однакову структуру.
Це означає, що відображення:
 :
:
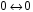 ,
,
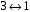 ,
є
ізоморфізмом кілець.
,
є
ізоморфізмом кілець.
Таким
чином,
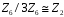 .
.