
- •Виконав(ла): студент(ка) бсдм(с)(убдм(с)) – 51
- •Властивості бінарних алгебраїчних операцій
- •2. Групи
- •3. Кільця
- •4. Поля
- •5. Ізоморфізми та гомоморфізми алгебраїчних структур
- •6. Векторні простори. Алгебри
- •Означення. Лінійною комбінацією векторів векторного простору називається вектор вигляду
- •1. Бінарні алгебраїчні операції
- •2. Групи
- •Симетрична і знакозмінна групи
- •3,4. Кільця і поля
- •5. Ізоморфізми та гомоморфізми алгебраїчних структур
- •6. Векторні простори. Алгебри
5. Ізоморфізми та гомоморфізми алгебраїчних структур
Означення.
Нехай
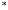 – алгебраїчна операція, задана на
множині
– алгебраїчна операція, задана на
множині
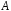 ,
,
 –
алгебраїчна операція, задана на множині
–
алгебраїчна операція, задана на множині
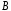 ,
,
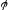 – відображення множини
– відображення множини
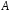 в множину
в множину
 .
Кажуть,
що відображення
.
Кажуть,
що відображення
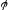 зберігає алгебраїчну операцію
зберігає алгебраїчну операцію
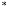 ,
якщо для будь-яких елементів
,
якщо для будь-яких елементів
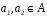 справедливо
справедливо
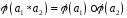 .
.
Означення.
Дві
групи
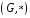 і
і
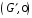 називаються гомоморфними,
якщо існує відображення
називаються гомоморфними,
якщо існує відображення
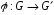 ,
при якому зберігається групова операція,
тобто таке, що:
,
при якому зберігається групова операція,
тобто таке, що:
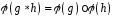 ;
;
Відображення, що задовольняє називається гомоморфізмом.
Означення.
Дві
групи
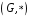 і
і
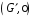 називаються ізоморфними,
якщо існує взаємно однозначне відображення
називаються ізоморфними,
якщо існує взаємно однозначне відображення
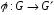 ,
при якому зберігається групова операція,
тобто таке, що:
,
при якому зберігається групова операція,
тобто таке, що:
1)
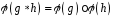 ;
;
2)
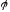 – бієкція.
– бієкція.
Відображення, що задовольняє умовам 1) і 2), називається ізоморфізмом.
Факт
ізоморфізму груп позначається символічно
 .
.
Теорема
(Келі).
Будь-яка скінченна група порядку
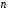 ізоморфна
деякій підгрупі симетричної групи
ізоморфна
деякій підгрупі симетричної групи
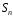 .
.
Означення.
Два кільця
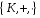 і
і
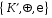 називаються гомоморфними,
якщо існує відображення
називаються гомоморфними,
якщо існує відображення
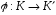 ,
при якому зберігаються операції, тобто
таке, що:
,
при якому зберігаються операції, тобто
таке, що:
1)
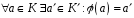 ;
;
2)
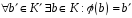 ;
;
3)
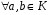
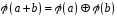 ,
,
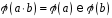 .
.
Відображення, що задовольняє умові, називається гомоморфним відображенням, або просто гомоморфізмом.
Означення гомоморфізму кілець можна сформулювати й іншим чином:
Означення.
Два
кільця
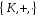 і
і
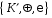 називаються гомоморфними,
якщо існує гомоморфізм адитивної групи
кільця
називаються гомоморфними,
якщо існує гомоморфізм адитивної групи
кільця
 на адитивну
групу кільця
на адитивну
групу кільця
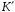 ,
що зберігає операцію множення.
,
що зберігає операцію множення.
Означення.
Два
кільця
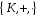 і
і
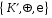 називаються ізоморфними,
якщо існує гомоморфне взаємно однозначне
відображення
називаються ізоморфними,
якщо існує гомоморфне взаємно однозначне
відображення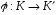 .
.
Факт
ізоморфізму кілець
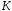 і
і
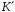 позначається символічно
позначається символічно
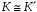 .
.
Означення.
Два поля
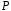 і
і
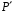 називаються ізоморфними,
якщо вони
ізоморфні як кільця.
називаються ізоморфними,
якщо вони
ізоморфні як кільця.
6. Векторні простори. Алгебри
Означення.
Множина
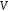 називається векторним
(лінійним)
простором,
якщо в
називається векторним
(лінійним)
простором,
якщо в
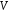 визначені алгебраїчна операція додавання
і операція множення на числа з поля
визначені алгебраїчна операція додавання
і операція множення на числа з поля
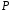 ,
причому виконані наступні умови (аксіоми
векторного простору):
,
причому виконані наступні умови (аксіоми
векторного простору):
1.
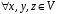
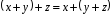 – асоціативність додавання;
– асоціативність додавання;
2.
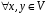
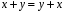 – комутативність додавання ;
– комутативність додавання ;
3.
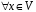
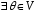 :
:
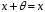 – існування нульового елемента ;
– існування нульового елемента ;
4.
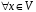
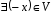 :
: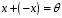 – існування протилежного елемента;
– існування протилежного елемента;
5.
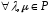
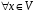
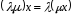 – асоціативність множення на число;
– асоціативність множення на число;
6.
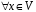
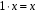 .
.
7.
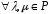

 – дистрибутивність відносно додавання
чисел ;
– дистрибутивність відносно додавання
чисел ;
8.
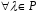
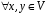
 – дистрибутивність відносно додавання
елементів;
– дистрибутивність відносно додавання
елементів;
Елементи
векторного простору називаються
векторами,
елемент
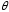 називається
нульовим вектором (нуль-вектором).
називається
нульовим вектором (нуль-вектором).
Означення. Лінійною комбінацією векторів векторного простору називається вектор вигляду
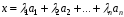 . (1)
. (1)
де
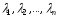 – деякі числа з поля
– деякі числа з поля
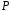
Означення.
Система векторів
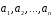 векторного простору
векторного простору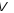 називається лінійно
залежною,
якщо існують числа
називається лінійно
залежною,
якщо існують числа
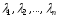 ,
які не всі водночас дорівнюють нулю
(
,
які не всі водночас дорівнюють нулю
(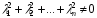 ),
такі що
),
такі що
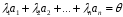 (2)
(2)
Система
векторів
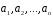 називається лінійно
незалежною,
якщо остання рівність виконується
тільки в одному випадку , коли
називається лінійно
незалежною,
якщо остання рівність виконується
тільки в одному випадку , коли
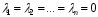
Означення.
Впорядкована система векторів
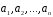 називається базисом
векторного простору
називається базисом
векторного простору
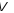 ,
якщо
,
якщо
1) вона лінійно незалежна;
2)
кожен вектор
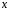 простору
простору
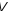 лінійно виражається через вектори цієї
системи, тобто
лінійно виражається через вектори цієї
системи, тобто
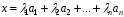 .
.
Означення.
Векторний простір
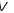 називається
називається
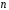 -вимірним,
якщо в ньому існує базис з
-вимірним,
якщо в ньому існує базис з
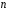 елементів. Число
елементів. Число
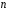 називається розмірністю
простору і позначається
називається розмірністю
простору і позначається
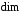
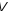 .
.
Теорема
(про зв'язок між базисом і розмірністю).
Система
векторів
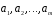 утворює в просторі
утворює в просторі
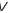 розмірності
розмірності
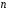 базис тоді і тільки тоді, коли вона
лінійно незалежна, а число векторів в
ній дорівнює розмірності простору
базис тоді і тільки тоді, коли вона
лінійно незалежна, а число векторів в
ній дорівнює розмірності простору
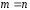 .
.
Якщо
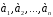 – деякий базис векторного простору
– деякий базис векторного простору
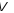 ,
то будь-який вектор
,
то будь-який вектор
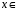
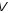 можна розкласти за цим базисом, тобто
подати у вигляді
можна розкласти за цим базисом, тобто
подати у вигляді
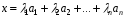
де
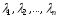 – деякі дійсні числа, причому єдиним
чином.
– деякі дійсні числа, причому єдиним
чином.
Означення.
Непорожня
підмножина
 векторного простору
векторного простору
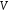 називається
підпростором
простору
називається
підпростором
простору
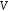 ,
якщо воно є векторним простором відносно
операцій, визначених в
,
якщо воно є векторним простором відносно
операцій, визначених в
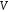 .
.
Теорема
(критерій підпростору). Непорожня
підмножина
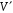 векторного простору
векторного простору
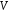 є
підпростором простору
є
підпростором простору
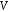 оді і тільки тоді, коли виконується
наступні умови:
оді і тільки тоді, коли виконується
наступні умови:
-
Якщо
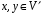 ,
то
,
то
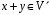 ;
; -
Якщо
 ,
,
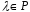 то
то
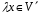 .
.
Означення.
Алгеброю
(лінійною алгеброю)
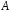 над полем
над полем
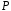 називається векторний простір
називається векторний простір
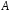 ,
в якому визначена алгебраїчна операція
множення векторів, причому виконані
наступні умови (аксіоми алгебри):
,
в якому визначена алгебраїчна операція
множення векторів, причому виконані
наступні умови (аксіоми алгебри):
1.
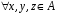
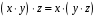 – асоціативність множення;
– асоціативність множення;
2.
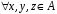
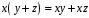 – дистрибутивність справа відносно
додавання векторів;
– дистрибутивність справа відносно
додавання векторів;
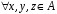
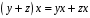 – дистрибутивність
зліва відносно додавання векторів;
– дистрибутивність
зліва відносно додавання векторів;
3.
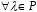
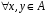
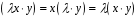 – дистрибутивність відносно множення
на число.
– дистрибутивність відносно множення
на число.
Можна дати інше означення алгебри, яке використовує поняття кільця:
Означення.
Алгеброю
(лінійною алгеброю)
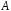 над полем
над полем
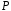 називається кільце з одиницею, яке
водночас є векторним простором
називається кільце з одиницею, яке
водночас є векторним простором
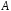 над полем
над полем
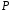 .
.
При
цьому аксіома 3 зв'язує множення на
елементи з поля
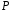 з множенням в кільці.
з множенням в кільці.
Означення.
Дві алгебри
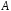 і
і
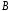 називаються ізоморфними,
якщо існує взаємно однозначне лінійне
відображення (ізоморфізм)
називаються ізоморфними,
якщо існує взаємно однозначне лінійне
відображення (ізоморфізм)
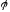 векторного простору
векторного простору
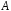 на векторний простір
на векторний простір
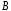 ,
яке зберігає операцію множення, тобто
таке, що для будь-яких елементів
,
яке зберігає операцію множення, тобто
таке, що для будь-яких елементів
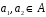
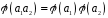
Очевидно,
що існування ізоморфізму
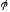 рівносильне тому, що в алгебрах
рівносильне тому, що в алгебрах
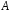 і
і
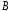 можна вибрати базиси з однаковими
таблицями множення.
можна вибрати базиси з однаковими
таблицями множення.
Означення.
Зображенням
скінченновимірної алгебри
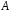 над полем
над полем
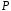 в скінченновимірному просторі
в скінченновимірному просторі
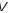 над полем
над полем
 називається гомоморфізм алгебри
називається гомоморфізм алгебри
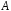 в алгебру лінійних операторів
(автоморфізми) простору
в алгебру лінійних операторів
(автоморфізми) простору
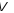
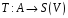 ,
,
тобто
відображення, яке задовольняє умовам:
для будь-яких
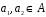 ,
,
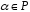
1)
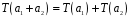 ;
;
2)
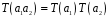 ;
;
3)
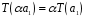 ;
;
4)
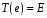 ,
де
,
де
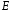 – тотожний оператор.
– тотожний оператор.
Означення.
Матричним
зображенням
степеня
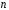 скінченновимірної алгебри
скінченновимірної алгебри
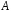 над полем
над полем
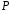 називається гомоморфізм алгебри
називається гомоморфізм алгебри
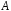 в алгебру
в алгебру
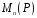 квадратних матриць порядку
квадратних матриць порядку
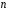 .
.
ІІ. Практичні завдання.
