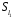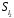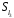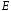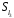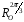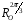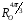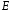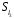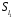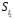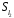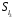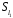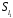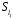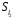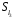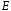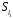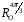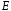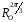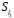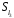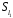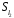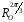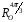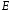- •Виконав(ла): студент(ка) бсдм(с)(убдм(с)) – 51
- •Властивості бінарних алгебраїчних операцій
- •2. Групи
- •3. Кільця
- •4. Поля
- •5. Ізоморфізми та гомоморфізми алгебраїчних структур
- •6. Векторні простори. Алгебри
- •Означення. Лінійною комбінацією векторів векторного простору називається вектор вигляду
- •1. Бінарні алгебраїчні операції
- •2. Групи
- •Симетрична і знакозмінна групи
- •3,4. Кільця і поля
- •5. Ізоморфізми та гомоморфізми алгебраїчних структур
- •6. Векторні простори. Алгебри
1. Бінарні алгебраїчні операції
Завдання
1.
У множині
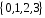 задано бінарну операцію
задано бінарну операцію
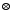 так, що
так, що
 є остачею від ділення добутку
є остачею від ділення добутку
 на число 4.
на число 4.
а)
Задати бінарну операцію
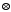 таблицею Келі.
таблицею Келі.
б)
Визначити властивості операції
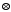 ;
;
в)
Визначити елементи, виділені відносно
операції
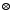 .
.
Розв'язання.
а)
Таблиця Келі для операції
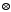 у множині
у множині
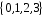 має вигляд:
має вигляд:
|
|
0 |
1 |
2 |
3 |
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
2 |
3 |
|
2 |
0 |
2 |
0 |
2 |
|
3 |
0 |
3 |
2 |
1 |
б)
Властивості операції
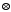 :
:
Операція
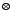 у множині
у множині
 є комутативною, оскільки її таблиця
Келі симетрична відносно діагоналі.
є комутативною, оскільки її таблиця
Келі симетрична відносно діагоналі.
в)
Визначити елементи, виділені відносно
операції
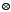 .
.
Щоб
визначити нейтральний елемент, знайдемо
стовпець таблиці Келі, що цілком
збігається з початковим. В таблиці для
операції
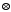 такий стовпець є, і йому відповідає
елемент 1. Отже, елемент 1 є нейтральним
відносно операції
такий стовпець є, і йому відповідає
елемент 1. Отже, елемент 1 є нейтральним
відносно операції
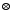 .
.
Щоб визначити існування симетричного елемента для даного, рухаємося по рядку, який відповідає даному елементу, до нейтрального елемента. Зверху, у початковому рядку, напроти нейтрального елемента знаходиться шуканий симетричний.
Для
елемента 2 не існує симетричного, оскільки
2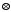 0=2
0=2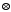 2=0
і 2
2=0
і 2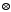 1=2
1=2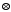 3=2.
3=2.
2. Групи
Завдання 2.
1. Довести, що множина всіх цілих степенів числа 2 є групою відносно операції множення.
Доведення.
Нехай
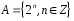 – множина всіх цілих степенів числа 2.
Операція множення степенів числа 2 є
алгебраїчною, тому що
– множина всіх цілих степенів числа 2.
Операція множення степенів числа 2 є
алгебраїчною, тому що
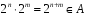
Перевіримо аксіоми групи.
1) Операція множення степенів числа 2 є асоціативною (властивості степенів).
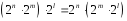
2)
Нейтральний елемент
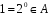 .
.
3)
Симетричний елемент
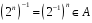 .
.
Таким
чином,
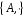 – група.
□
– група.
□
2. Довести, що множина всіх симетрій правильного трикутника є групою відносно операції композиції симетрій. Скласти таблицю Келі.
Доведення.
Множина
всіх симетрій правильного трикутника
складається з тотожного перетворення
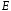 ,
поворотів
,
поворотів
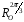 ,
,
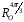 і трьох осьових симетрій (віддзеркалень)
і трьох осьових симетрій (віддзеркалень)
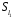 ,
,
 ,
,
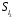 .
Отже,
.
Отже,
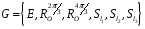
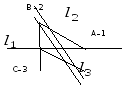
Складемо таблицю Келі:
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Операція композиції симетрій правильного трикутника є алгебраїчною.
Перевіримо аксіоми групи.
1) Операція композиції симетрій правильного трикутника є асоціативною (властивості композиції симетрій).
Наприклад, перевіримо, що
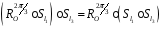 .
.
За таблицею Келі
 ,
,
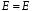 .
.
2)
Нейтральний елемент:
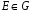 .
.
3)
Симетричний елемент:
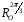 –
–
 ,
,
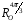 –
–
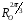 ,
,
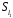 –
–
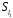 ,
,
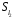 –
–
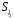 ,
,
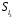 –
–
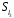 .
.
Таким
чином,
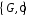 – група.
□
– група.
□