Метод множителей Лагранжа

С помощью метода множителей Лагранжа по существу устанавливаются необходимые условия, позволяющие идентифицировать точки оптимума в задачах оптимизации с ограничениями в виде ра­венств. При этом задача с ограничениями преобразуется в эквива­лентную задачу безусловной оптимизации, в которой фигурируют некоторые неизвестные параметры, называемые множителями Ла­гранжа.

Пусть задана задача математического программирования: максимизировать (минимизировать) функцию (3)

при ограничениях . (4)

Ограничения в задаче заданы уравнениями, поэтому для ее решения можно воспользоваться классическим методом отыскания условного экстремума функций нескольких переменных. При этом полагаем, что функции и непрерывны вместе со своими первыми частными производными.

Вводим набор переменных , называемых множителями Лагранжа и составляем функцию Лагранжа:

. (5)

Определяем частные производные и рассматриваем систему уравнений (6) с неизвестными .

Всякое решение системы (6) определяет точку , в которой может иметь место экстремум функции. Следовательно, решив систему (6), получают все точки, в которой функция (3) может иметь экстремальные значения. При этом неизвестен способ определения точек глобального минимума или максимума. Дальнейшее исследование найденных точек проводят так же, как и в случае безусловного экстремума, т.е. если для функции (3) существуют вторые частные производные и они непрерывны, то можно вывести достаточное условие существования локального экстремума функции в точке, являющейся решением системы (6). Однако практическое значение этого условия невелико.

Метод множителей Лагранжа имеет ограниченное применение, так как система (6), как правило, имеет несколько решений.

Пример 3.

Найти точки экстремума функции при условии .

Составим функцию Лагранжа .

Найдем ее частные производные по , приравнивав их к нулю:

Решение системы . Таким образом, в точке данная функция может иметь условный экстремум.

Найдем .

Далее .

Так как и , то в точке имеем условный минимум, причем .

Пример 4.

Обработка статистических данных показала, что производственная функция, связывающая выпуск готовой продукции предприятия с численностью рабочих и производственными фондами , имеет вид . Общие затраты предприятия на заработную плату и оборудование определяются соотношением .

Нужно определить затраты предприятия на покупку оборудования и расходы на заработную плату, при которых выпуск продукции будет максимальным.

Для решения составляем функцию Лагранжа:

.

Находим частные производные этой функции по и, исходя из необходимого условия экстремума функции Лагранжа, приравниваем их к нулю.

Получим систему:

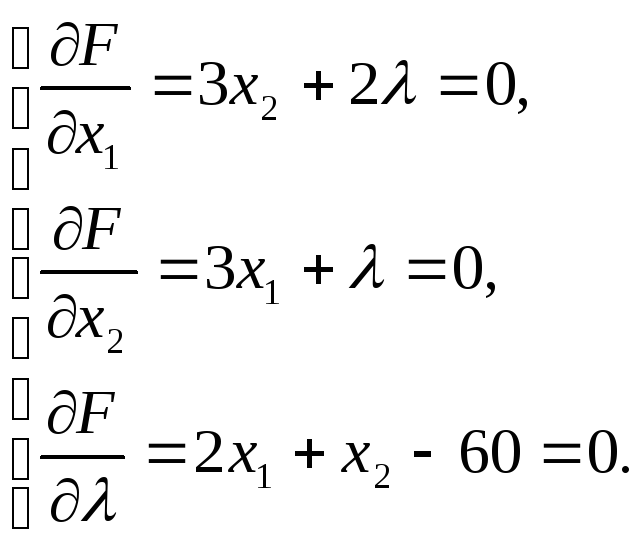
Отсюда и тогда . Находим, что . Получаем .

Теперь необходимо убедиться, что в точке (15;30) функция F достигает max. Для этого рассмотрим окрестность точки (15;30) и составим приращение функции

.

Так как по условию , или , то ,или .

Подставим это соотношение в :

при любом .

Это показывает, что в точке функция Лагранжа достигает max, равного .