2.3. Метод хорд (секущих)

Предполагая опять, что f(x) непрерывна на отрезке [a,b] и имеет разные знаки на его концах, получим формулы для приближенного вычисления корня уравнения (2.1), учитывающие не только знаки f(x), но и ее значения. Для этого соединим точки хордой АВ (рис. 2.1). Точку пересечения х₁ этой хорды с осью абсцисс примем за приближенное значение корня.

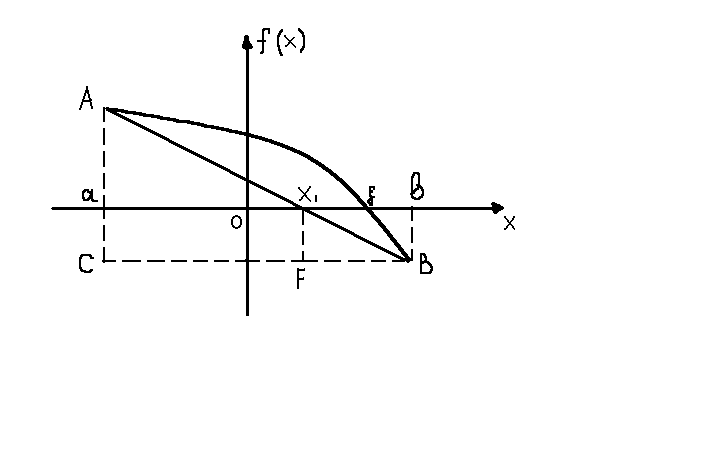
Рис.2.1.

Из подобия треугольников АВС и , АВС и следуют соотношения

,

откуда получим соответственно две формулы метода хорд для х₁:

(2.7)

(2.8)

Выбрав одну из формул, (2.7) или (2.8), вычислим х₁, определим знак и, как в методе половинного деления, для дальнейших вычислений выберем тот из отрезков , на концах которого функция имеет разные по знаку значения. Оценкой абсолютной погрешности приближенного значения х₁ здесь может служить величина

,

Получим еще одну оценку абсолютной погрешности при дополнительном предположении, что на отрезке [a, b] f(x) дифференцируема и

где  - точка, расположенная между корнем  и х_1.

Отсюда

. (2.9)

Если уравнение (2.1) имеет на отрезке [a, b] несколько корней, то метод хорд, как и метод половинного деления, вычислит с точностью до один из них. Если же функция f(x) имеет на отрезке [a, b] непрерывную первую и вторую производные, сохраняющие свои знаки, то можно показать [5], что последовательность приближенных значений метода хорд, построенная по формуле

, (2.10)

где с - один из концов отрезка [a, b], удовлетворяющий условию

,

а x₀ - противоположный конец отрезка, сходится к единственному на этом отрезке корню уравнения (2.1) монотонно.

2.4. Метод касательных (метод Ньютона)

Пусть искомый корень уравнения (2.1) принадлежит отрезку [a, b], . Представим f() с помощью разложения функции f(x) в ряд Тейлора в окрестности точки x₀

, (2.11)

где  - точка, находящаяся между точками  и x₁. Пренебрегая в (2.11) остаточным членом, найдем приближенное значение x₁ корня :

. (2.12)

Подставив в правую часть (2.12) вместо x₀ полученное значение x₁, получим x₂ и т.д. Докажем, что последовательность

(2.13)

монотонно сходится к единственному на отрезке корню  уравнения (2.1), если:

1) ;

2) непрерывны, отличны от нуля и сохраняют свои знаки на [a, b];

3) начальное приближение x₀ удовлетворяет условию: . Существование и единственность корня следуют из условий I и 2.

Докажем сходимость последовательности (2.13) для случая, когда (рис. 2.2)

.

В остальных случаях доказательство ведется аналогичным образом.

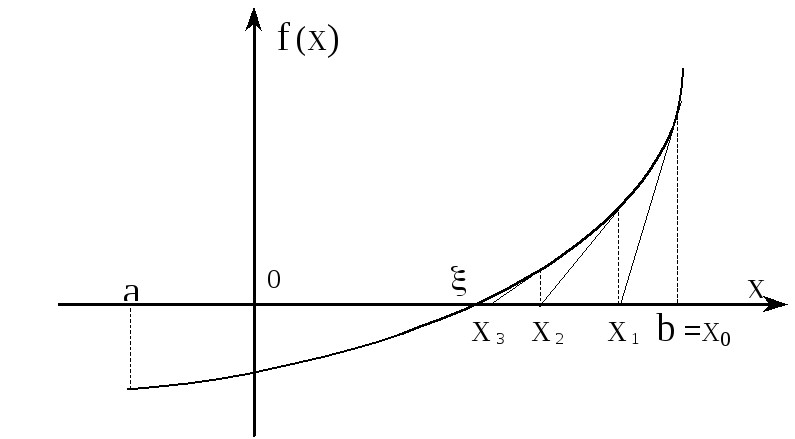
Рис. 2.2.

За начальное приближение удобно взять один из концов отрезка [a, b],. В данном случае , так как . Методом индукции докажем, что последовательность , построенная по формуле (2.13), ограничена снизу точным корнем  .Действительно, . Допустим, что все приближения и докажем, что . Разложим функцию f(x) в ряд Тейлора в окрестности точки :

, (2.14)

где точка  расположена между x и . Подставим в (2.14) x = 

.

Поскольку на [a, b],

,

откуда

,

т.е. ограниченность снизу последовательности доказана. Отсюда т.е. – последовательность , монотонно убывает и, значит, имеет предел:

.

Перейдем к пределу при в равенстве (2.13)

,

Абсолютную погрешность приближения , полученного методом касательных, можно оценить формулой (2.9). Преобразуем эту оценку с помощью (2.13). Представим f(x_n)разложением в ряд Тейлора в окрестности точки :

,

где  - точка, расположенная между и .

Согласно (2.13)

или ,

откуда

.

Обозначим .

Получим следующую оценку абсолютной погрешности величины :

.

На свойстве монотонности последовательностей метода хорд (2.10) и метода касательных (2.13) основан комбинированный метод, заключающийся в одновременном использовании этих двух методов:

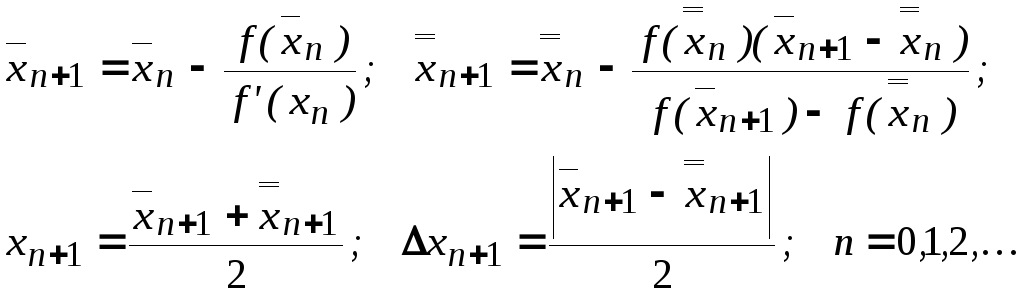
Если в формуле (2.13) положить

,

то формула (2.13) примем вид

Эта модификация метода касательных носит название двухшагового метода хорд.