7.2. Разностный метод решения краевой задачи

Рассмотрим краевую задачу для дифференциального уравнения второго порядка следующего вида:

(7.25)

(7.26)

зададим шаг , n – целое. Точки , примем за узлы сетки, – неизвестные значения искомого решения в узлах. Выразим производную в узлах сетки по формуле численного дифференцирования

.

Пусть

.

Вместо дифференциальной краевой задачи (7.25)-(7.26) будем иметь разностную краевую задачу

(7.27)

(7.28)

где y_j – приближенное значение точного решения y(x_j) в узлах .

Перепишем систему линейных алгебраических уравнений (7.27)-(7.28) в виде

.

Эта система с трех диагональной матрицей при на [0, H] имеет решение, причем единственное, которое может быть получено методом прогонки, при этом условие гарантирует устойчивость прогонки. Дадим оценку этому решению.

Лемма 1. Пусть и числа таковы, что . Тогда для всех j. Пусть . Предположим, что . Следовательно, . Пусть q – наименьшее целое, для которого . Из определения d и q имеем: .

Тогда

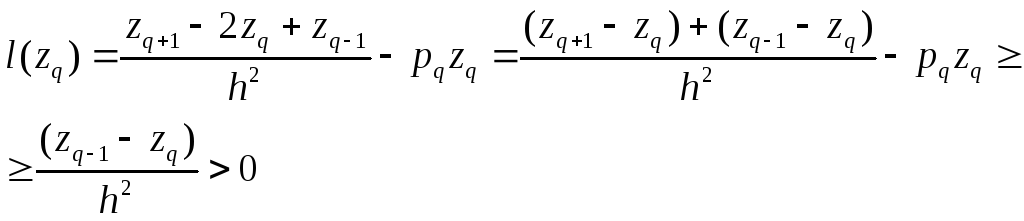
- противоречие с .

Лемма 1 доказана.

Лемма 2. Если , то для любой системы чисел z_j выполняется неравенство

,

где .

Введем в рассмотрение функцию

Через обозначим

.

Очевидно, что .

Это многочлен второй степени. Для него конечная разность второго порядка , следовательно,

.

Отсюда следует, что

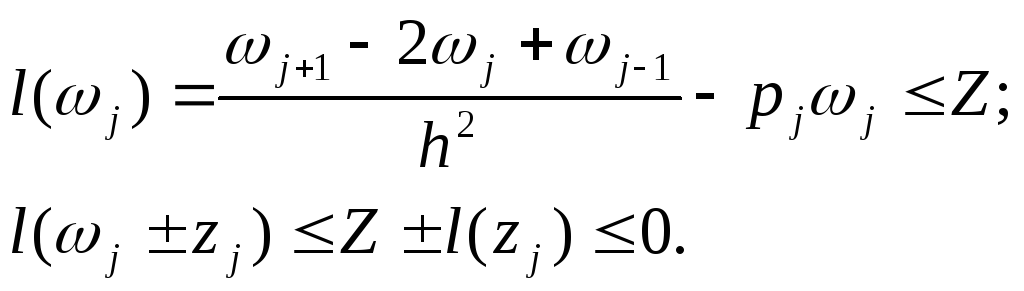
Очевидно, что

.

Числа удовлетворяют условиям леммы 1. Поэтому . Отсюда следует оценка

.

Имеем неравенство

.

Кроме того,

.

Поэтому имеем

.

Лемма 2 доказана.

Рассмотрим случай, когда функции P(x) и f(x) дважды непрерывно дифференцируемы. В курсе дифференциальных уравнений доказывается, что когда краевая задача (7.25)-(7.26) имеет единственное решение y(x), которое четырежды непрерывно дифференцируемо. Наша задача – оценить разность для . – это краевые условия.

Рассмотрим

Согласно дифференциальному уравнению (7.25) для любого j

Следовательно,

Левая часть этого равенства есть разность между приближенным значением второй производной в точке x_j, полученным по формуле численного дифференцирования, и точным значением этой производной y(x_j) и равна остаточному члену этой формулы

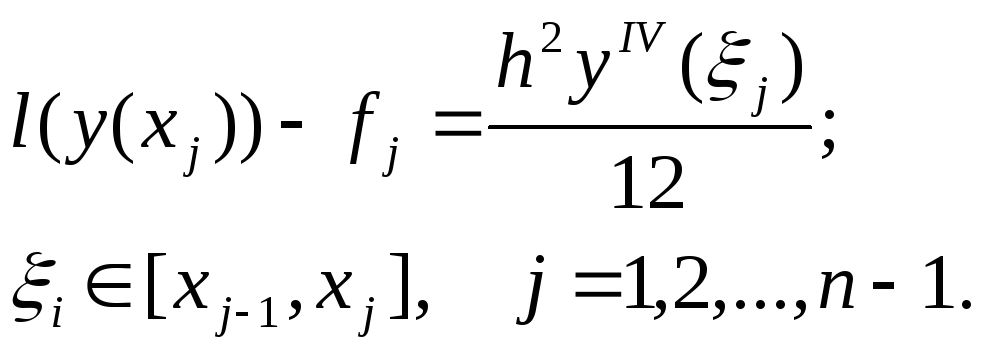(7.29)

Согласно (7.27) имеем

. (7.30)

Вычтем (7.30) из (7.29)

т.е.

.

Воспользуемся леммой 2 для чисел . Имеем

.

Таким образом, при , т.е. неограниченном сгущении сетки, решение разностной задачи приближается к решению дифференциальной.

Разностный метод решения краевой задачи (7.25)-(7.26) используется также и при , хотя успешный результат заранее предвидеть трудно. Для оценки получаемого решения в этом случае нужно провести расчеты для различных значений шага h (не менее трех) и убедиться в том, что полученные значения функции в одних и тех же узлах близки между собой и их разность уменьшается, что говорит о стремлении решения к некоторому пределу при .

Список литературы

1. Бахвалов Н.С. Численные методы. –М: Наука, 1975.

2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – М.: Лаборатория Базовых Знаний, 2001.

3. Березин И.С., Жидков Н.П. Методы вычислений. – Т.1. – М.: Наука, 1966; - Т.2. – М.: Физматгиз, 1962.

4. Волков Е.А. Численные методы. – М.: Наука, 1987.

5. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Наука, 1970.

6. Демидович Б.П., Марон И.А., Шувалова Э.З. численные методы анализа. – М: Наука, 1967.

7. Калиткин Н.Н., Численные методы. - М.: Наука, 1978.

8. Курош А.Г. Курс высшей алгебры. - М.: Наука, 1968.

9. Самарский А.А., Гулин А.В. Численные методы. – М: Наука, 1989.

10. Турчак Л.И. Основы численных методов. – М: Наука, 1987.

11. Фаддеев Д.К., Фаддеева В.Н. вычислительные методы линейной алгебры. – М: Физматгиз, 1963.

12. Фихтенгольц Г.М. Математический анализ. –Т.1, 2. – М: Гостехиздат, 1957.

13. Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений. – М: Мир, 1980.

102