- •Министерство образования российской федерации
- •Московский международный институт эконометрики, информатики, финансов и права
- •И.Н. Мастяева о.Н. Семенихина
- •Численные методы
- •Учебное пособие
- •Москва 2004
- •Содержание:
- •1. Погрешность результата численного решения задачи
- •1.1. Источники и классификация погрешностей.
- •1.2. Точные и приближенные числа. Правила округления чисел
- •1.3. Математические характеристики точности приближенных чисел
- •1.4. Число верных знаков приближенного числа. Связь абсолютной и относительной погрешности с числом верных знаков. Правила подсчета числа верных знаков
- •5423,47 6 Значащих цифр,
- •0,0000605 3 Значащие цифры,
- •0,060500 5 Значащих цифр.
- •1.5. Общая формула теории погрешностей (погрешность вычисления значения функции)
- •1.6. Погрешность арифметических действий
- •1.7. Обратная задача теории погрешностей
- •2. Численные методы решения нелинейных уравнений
- •2.1. Отделение корней
- •2.2. Метод половинного деления
- •2.3. Метод хорд (секущих)
- •2.4. Метод касательных (метод Ньютона)
- •2.5. Метод итераций
- •3. Численные методы линейной алгебры
- •3.1. Метод Гаусса
- •З.2. Метод прогонки
- •3.3. Норма вектора и норма матрицы
- •3.4. Метод простой итерации
- •3.5. Частичная проблема собственных значений
- •Интерполирование.
- •4.1. Интерполяционный полином, его существование и единственность. Остаточный член.
- •4.2. Интерполяционный полином Лагранжа.
- •4.3. Разделенные разности и их свойства.
- •4.4. Интерполяционный полином Ньютона с разделенными разностями
- •4.5. Конечные разности и их свойства
- •4.6. Интерполяционные формулы Ньютона
- •4.7. Интерполяционные полиномы с центральными разностями
- •4.8.Обратное интерполирование
- •4.9. Численное дифференцирование
- •5. Интерполирование с кратными узлами и сплайны
- •5.1. Разделенные разности с повторяющимися (кратными) узлами
- •5.2. Интерполяционный полином Эрмита
- •5.3. Интерполирование сплайнами
- •6. Численное интегрирование
- •6.1. Формула прямоугольников
- •6.2. Формула трапеций
- •6.3. Формула Симпсона
- •6.4. Правило Рунге практической оценки погрешности квадратурных формул. Уточнение приближенного значения интеграла по Ричардсону
- •7. Численные методы решения дифференциальных уравнений
- •7.1. Метод Рунге-Кутта
- •7.2. Разностный метод решения краевой задачи
- •Список литературы
4.6. Интерполяционные формулы Ньютона
Рассмотрим интерполяционный полином Ньютона с разделенными разностями (4.18), взяв в качестве узлов интерполирования равноотстоящие точки x0, x1 = x0+ h, …,xi=x0+ih,…,xn = x0+nh. Заменяя разделенные разности их выражениями через конечные разности согласно (4.20)
![]() ,
,
получим
![]()
Введем
переменную
![]() .
Тогда формула примет вид
.
Тогда формула примет вид
![]() .
(4.22)
.
(4.22)
Полученную формулу называют первым интерполяционным полиномом Ньютона или полиномом Ньютона для интерполирования вперед.
Остаточная
погрешность значения
![]() выражается формулой (4.8). Если заменить
выражается формулой (4.8). Если заменить
![]() ,
то она примет следующий вид:
,
то она примет следующий вид:
![]() .
.
На
практике величина
![]() оценивается согласно (4.21) с помощью
конечных разностей (п+1)-го
порядка
оценивается согласно (4.21) с помощью
конечных разностей (п+1)-го
порядка
![]()
или
![]() определяется абсолютной величиной
первого отброшенного слагаемого.
определяется абсолютной величиной
первого отброшенного слагаемого.
Введем
еще одну интерполяционную формулу
Ньютона. Для этого запишем полином
Ньютона с разделенными разностями
(4.18), присоединяя узлы в следующем
порядке:
![]() :
:
![]() Введем
переменную
Введем
переменную
![]() .
и выразим разделенные разности через
конечные.
.
и выразим разделенные разности через
конечные.
![]() . (4.23)
. (4.23)
Эта формула называется вторым интерполяционным полиномом Ньютона, или полиномом Ньютона для интерполирования назад.
Оценка
(4.8) остаточной погрешности приближенного
значения
![]() представится в виде
представится в виде
![]()
![]() .
.
Итак, получены две новые формулы интерполирования, и далее будут получен еще ряд таких формул. Однако следует заметить, что каждая из них является лишь другой формой записи интерполяционного полинома Лагранжа. Поэтому, если отвлечься от различия в обозначениях и в форме записи, то все эти формулы тождественны, когда они построены по одним и тем же узлам интерполирования. Однако в практике вычислений применяются в различных случаях разные формулы. Как уже отмечалось, во-первых, дело связано с тем, что обычно бывает удобнее вести вычисления, если при интерполировании сначала используются ближайшие к x* узлы, а затем подключаются все более удаленные. При этом первые члены интерполяционных формул дадут основной вклад в искомую величину, а остальные будут давать лишь уменьшающиеся (по модулю) добавки. В этом случае легко установить, на какой разности следует закончить вычисления.
Во-вторых,
как было отмечено в разделе 4.1, максимальные
значения
![]() убывают к середине отрезка, содержащего
все узлы, и возрастают к концам его.
Поэтому, если имеется возможность при
вычислениях для различных x
строить интерполяционный полином по
различным узлам, то их следует выбирать
так, чтобы точка x
находилась вблизи середины отрезка,
содержащего все узлы интерполирования.
В этом смысле мы можем сравнивать по
точности различные интерполяционные
формулы
убывают к середине отрезка, содержащего
все узлы, и возрастают к концам его.
Поэтому, если имеется возможность при
вычислениях для различных x
строить интерполяционный полином по
различным узлам, то их следует выбирать
так, чтобы точка x
находилась вблизи середины отрезка,
содержащего все узлы интерполирования.
В этом смысле мы можем сравнивать по
точности различные интерполяционные
формулы
4.7. Интерполяционные полиномы с центральными разностями
Возьмем
в качестве узлов интерполирования точки
![]() ,
где
,
где
![]() .
Построим интерполяционный полином
Ньютона с разделенными разностями
.
Построим интерполяционный полином
Ньютона с разделенными разностями
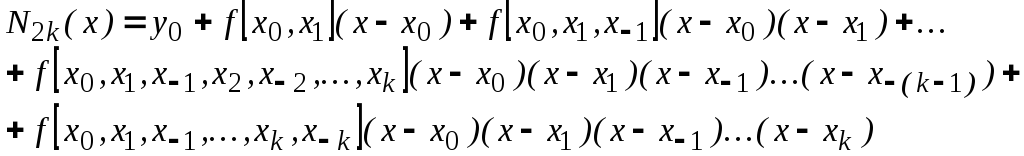
Используя симметричность разделенных разностей относительно своих аргументов и связь их с конечными разностями (4.20), получим

Отсюда

Введя
переменную
![]() ,
получим первый интерполяционный полином
Гаусса, или полином Гаусса для
интерполирования вперед,
,
получим первый интерполяционный полином
Гаусса, или полином Гаусса для
интерполирования вперед,
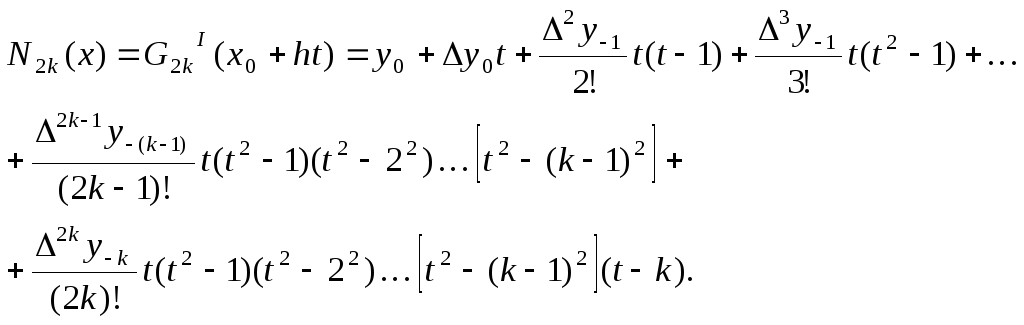 (4.24)
(4.24)
В этой формуле используются следующие конечные разности (подчеркнуты):
|
xi |
yi |
|
|
|
|
|
x-3 |
y-3 |
|
|
|
|
|
|
|
|
|
|
|
|
x-2 |
y-2 |
|
|
|
|
|
|
|
|
|
|
|
|
x-1 |
y-1 |
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
y0 |
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
y1 |
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
y3 |
|
|
|
|
Если
взять узлы интерполирования в другом
порядке, а именно
![]() ,
то совершенно аналогично можно получить
второй интерполяционный полином Гаусса,
или интерполяционный полином Гаусса
для интерполирования назад,
,
то совершенно аналогично можно получить
второй интерполяционный полином Гаусса,
или интерполяционный полином Гаусса
для интерполирования назад,
 (4.25)
(4.25)
Вторая интерполяционная формула Гаусса использует следующие конечные разности:
|
xi |
yi |
|
|
|
|
|
x-3 |
y-3 |
|
|
|
|
|
|
|
|
|
|
|
|
x-2 |
y-2 |
|
|
|
|
|
|
|
|
|
|
|
|
x-1 |
y-1 |
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
y0 |
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
y1 |
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
y3 |
|
|
|
|
Взяв полусумму интерполяционных формул Гаусса, получим интерполяционный полином Стирлинга в виде формулы:
 (4.26)
(4.26)
Интерполяционный полином Стирлинга использует следующие конечные разности:
|
xi |
yi |
|
|
|
|
|
x-3 |
y-3 |
|
|
|
|
|
|
|
|
|
|
|
|
x-2 |
y-2 |
|
|
|
|
|
|
|
|
|
|
|
|
x-1 |
y-1 |
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
y0 |
1/2 |
|
1/2 |
|
|
|
|
|
|
|
|
|
x1 |
y1 |
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
y3 |
|
|
|
|
Остаточный член интерполяционных формул (4.24), (4.25) и (4.26) имеет следующий вид
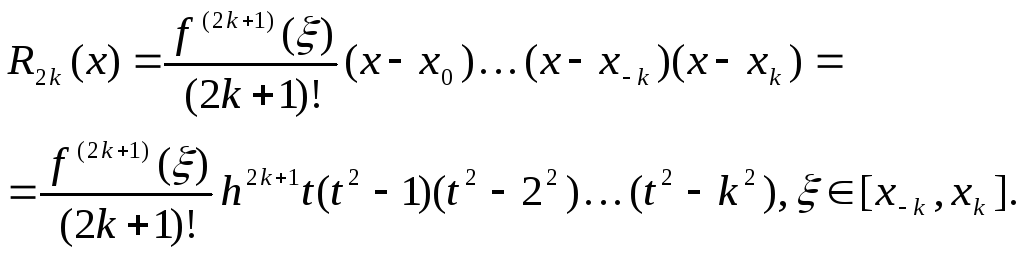 (4.27)
(4.27)
Например, для полинома Стирлинга второй степени
![]() ,
,
остаточный член
![]() .
.
Получим
еще одну форму интерполяционного
полинома. Для этого применим вторую
интерполяционную формулу Гаусса к точке
х1,
используя для ее построения узлы
![]() .
Тогда
.
Тогда
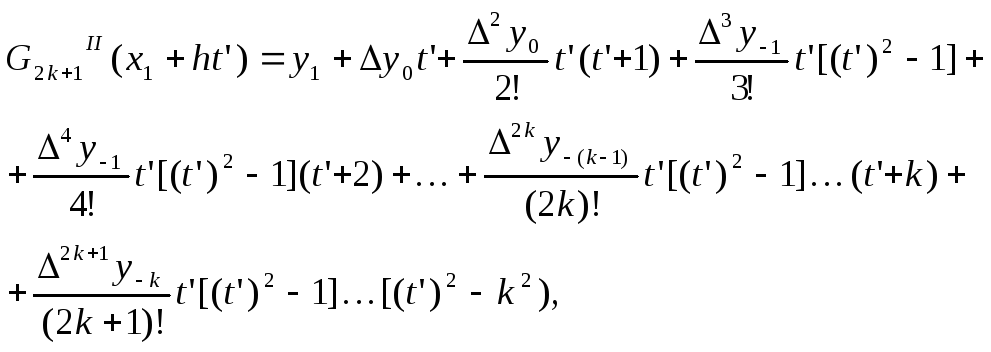
где
![]() .
Легко видеть, что
.
Легко видеть, что
![]() ,
где
,
где
![]() .
Выразим в
.
Выразим в
![]() через t.
Получим
через t.
Получим
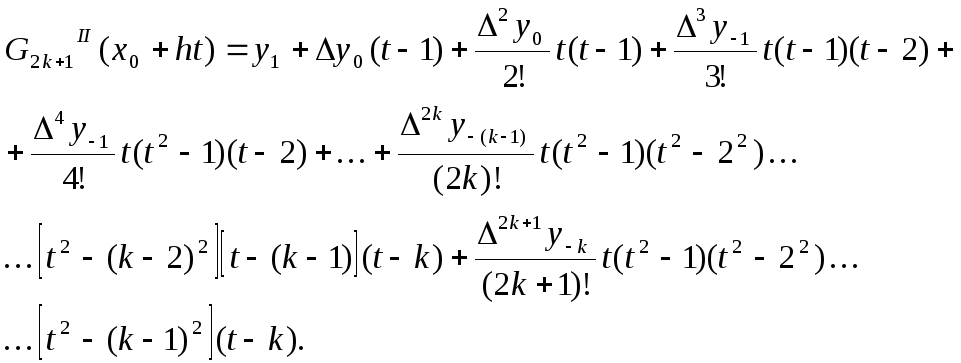
Полусумма
этой формулы и первой формулы Гаусса
(4.24), построенной по узлам
![]() ,
даст интерполяционный полином Бесселя:
,
даст интерполяционный полином Бесселя:
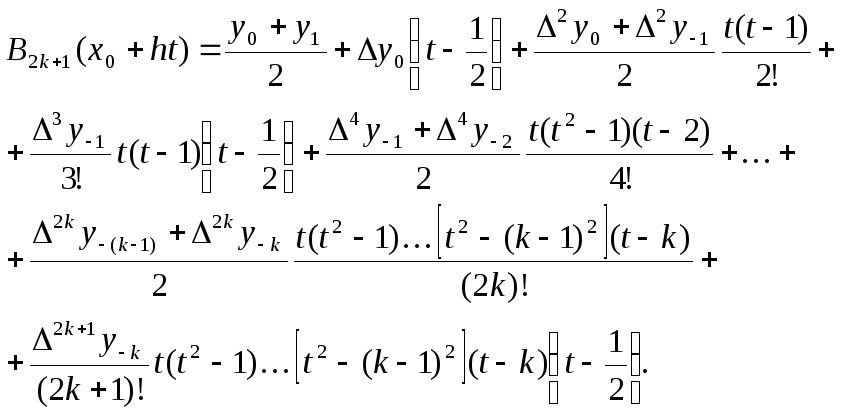 (4.28)
(4.28)
Полином
Бесселя особенно удобен для интерполирования
на середину, т.е. для
![]() .
Действительно, в этом случае члены,
содержащие разности нечетного порядка,
обращаются в нуль. В формуле Бесселя
используются следующие разности:
.
Действительно, в этом случае члены,
содержащие разности нечетного порядка,
обращаются в нуль. В формуле Бесселя
используются следующие разности:
|
xi |
yi |
|
|
|
|
|
|
x-3 |
y-3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x-2 |
y-2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x-1 |
y-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
y |
|
|
|
|
|
|
|
1/2 |
|
1/2 |
|
1/2 |
|
|
x1 |
y1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
y3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 |
y4 |
|
|
|
|
|
Остаточный член интерполяционного полинома Бесселя имеет вид
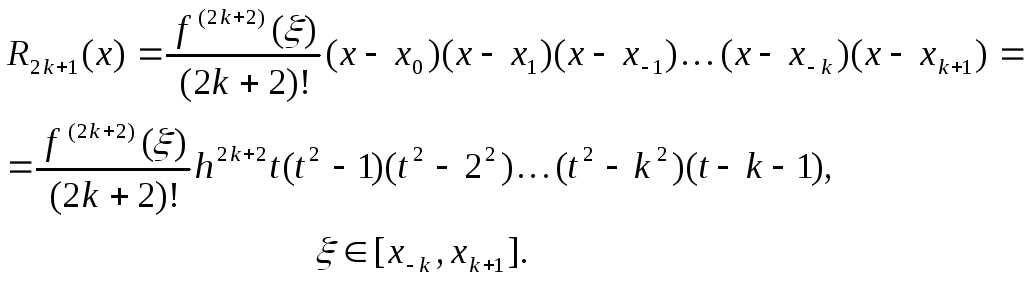 (4.29)
(4.29)
В частности, для полинома Бесселя первой и третьей степени
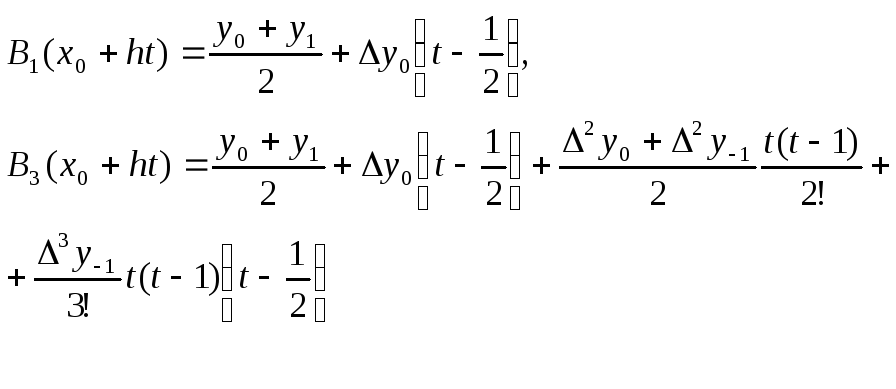
остаточные члены имеют вид
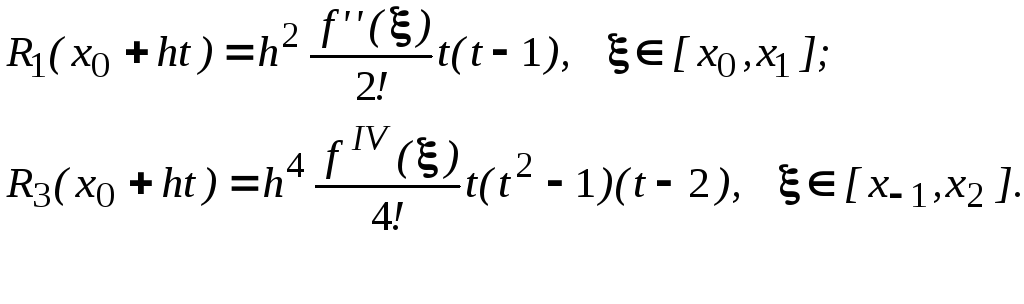

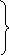
 0
0