4. Интерполирование.

Задача приближения (аппроксимации) функций возникает и как самостоятельная, и при решении многих других задач. Простейшая ситуация, приводящая к приближению функций, заключается в следующем. При некоторых значениях аргумента х₀, х₁,…х_n, называемых узлами, заданы значения функции y_i=f(x_i), i=0,1...,n. Требуется восстановить значения функции при других x. Подобная же задача возникает при многократном вычислении на ЭВМ одной и той же сложной функции в различных точках. Вместо этого часто бывает целесообразно вычислять значения этой функции в небольшом числе характерных точек x_i, а в остальных точках вычислять ее значения по некоторому более простому правилу, используя информацию об уже известных значениях y_i.

Другими распространенными примерами приближения функций являются задачи определения производной f'(x) и интеграла по заданным значениям y_i.

Классический подход к решению подобных задач заключается в том, чтобы, используя имеющуюся информацию о функции f(x), рассмотреть другую функцию , близкую к f(x), позволяющую выполнить над ней соответствующую операцию и получить оценку погрешности такой «аналитической замены».

При выборе класса, к которому принадлежит аппроксимирующая функция , следует руководствоваться тем, что , с одной стороны, должна отражать характерные особенности аппроксимируемой функции f(x), с другой стороны, быть достаточно удобной в обращении.

Вопрос о близости аппроксимируемой и аппроксимирующей функций решается по-разному. Если параметры, от которых зависит функция , определяются из условия совпадения значений функций f(x) и в узлах, то такой способ аппроксимации называется интерполированием (интерполяцией).

Наличие большого количества различных способов приближения объясняется многообразием различных постановок задачи. Далее мы рассмотрим лишь один раздел теории приближения – интерполирование многочленами. Аппарат интерполирования многочленами является важнейшим аппаратом численного анализа. На его основе строится большинство численных методов решения других задач.

4.1. Интерполяционный полином, его существование и единственность. Остаточный член.

Будем строить аппроксимирующую функцию в виде

. (4.1)

Коэффициенты определим из условий

. (4.2)

Распишем подробно эти условия:

.

……………..

.

Определитель этой системы

может быть получен из определителя Вандермонда

транспонированием матрицы и последующей перестановкой ее строк, т.е. будет отличаться от определителя Вандермонда лишь знаком.

Последний, как известно, равен [8], т.е. отличен от нуля, если узлы интерполирования x_i различны.

Следовательно, коэффициенты интерполяционного полинома (4.1) всегда могут быть определены, и при том единственным образом. Таким образом, доказано существование и единственность интерполяционного полинома (4.1).

Оценим остаточный член интерполирования

, (4.3)

где x* – точка, в которой значение функции вычисляется с помощью интерполяционного полинома.

Предположим, что узлы упорядочены: и непрерывна на [a, b], .

Введем вспомогательную функцию

, (4.4)

где константа выбирается так, чтобы

,

отсюда

. (4.5)

При таком выборе функция f(x) обращается в нуль в (п+2) точках . На основании теоремы Ролля ее производная F'(x) обращается в нуль, по крайней мере, в (п+1)-й точке. Применяя теорему Ролля к F'(x), получаем, что ее производная F''(x) обращается в нуль по крайней мере в п точках. Продолжая эти рассуждения дальше, получаем, что обращается в нуль по крайней мере в одной точке , принадлежащей отрезку [a, b]. Поскольку

,

из условия будем иметь

. (4.6)

Приравнивая правые части (4.5) и (4.6), получим представление остаточного члена в точке x^*

, (4.7)

где .

Остаточная абсолютная погрешность интерполирования в точке может быть оценена как

, (4.8)

где .

Так как точка – произвольная точка отрезка [a, b], выражение (4.7) остаточного члена справедливо для любой точки . Найдем оценку остаточной погрешности интерполирования на всем отрезке [a, b]:

,

где .

Оценить при произвольном расположении узлов интерполяции сложно. Если же узлы расположены на одинаковом расстоянии h друг от друга., то имеет примерно такой вид, как показано на рисунке 4.1. для п = 5 [3].

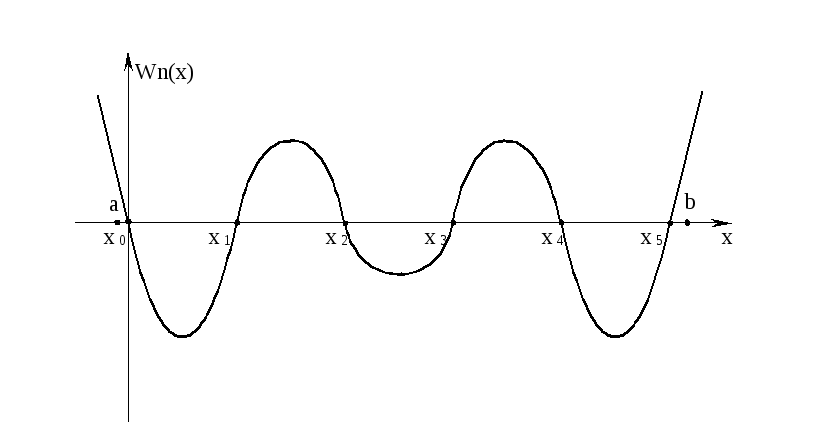
Рис. 4.1.

Вблизи центрального узла интерполяции экстремумы невелики, вблизи крайних узлов – несколько больше, а если Х выходит за крайние узлы интерполяции, то быстро возрастает. Термин «интерполяция» в узком смысле употребляют, если x заключен между крайними узлами; если же он выходит из этих пределов, то говорят об экстраполяции. Очевидно, что при экстраполяции далеко за крайним узлом ошибка может быть велика, поэтому экстраполяция малонадежна.