Нахождение функции по ее полному дифференциалу

Пусть на односвязной области (D) выполняется . Тогда на этой области дифференциальное выражение является полным дифференциалом некоторой функции F(x,y), т.е. . Из сказанного выше следует, что общий вид таких функций F(x,y):

,

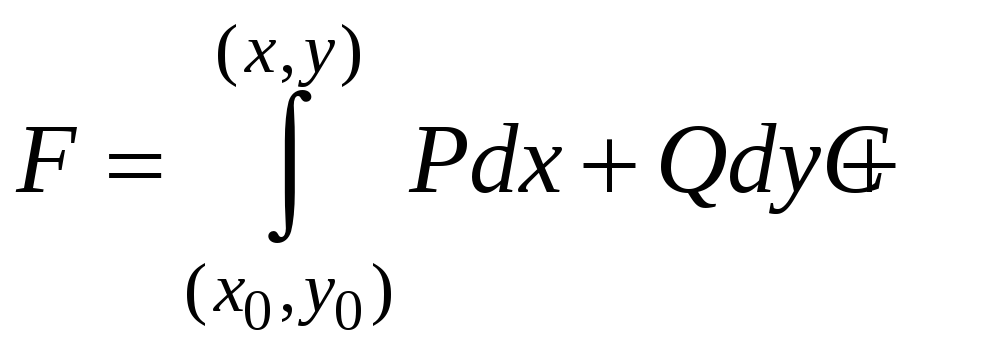причем интеграл не зависит от пути интегрирования на области (D).

В качестве пути интегрирования обычно выбирают ломаную с двумя звеньями, параллельными осям координат.

Примеры решения задач

Пример 1. Вычислить криволинейный интеграл , где (L) – контур треугольника ABC с вершинами .

Решение. Вычислим данный интеграл двумя способами: с помощью формулы Грина-Остроградского и непосредственно по теореме о вычислении криволинейных интегралов второго рода.

I. Если функции P(x,y) и Q(x,y) непрерывны вместе со своими частными производными и на простой области (D), то справедлива формула Грина-Остроградского

,

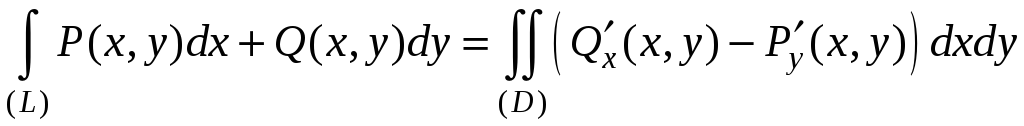связывающая криволинейный интеграл по замкнутому контуру (L) с двойным интегралом по области, ограниченной этим контуром. При этом интегрирование в криволинейном интеграле осуществляется в положительном направлении.

В данном интеграле

,,

.

Функции P(x,y) и Q(x,y) непрерывны вместе со своими частными производными и везде на R², следовательно, и на простой области (D), ограниченной контуром треугольника ABС. Тогда по формуле Грина-Остроградского получаем:

,

где область (D) – треугольник ABC.

Уравнение прямой AB: , уравнение прямой BC: . Вычислим двойной интеграл:

.

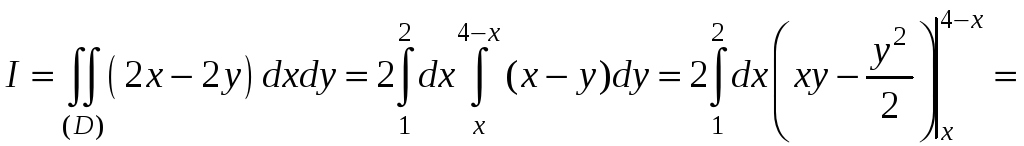
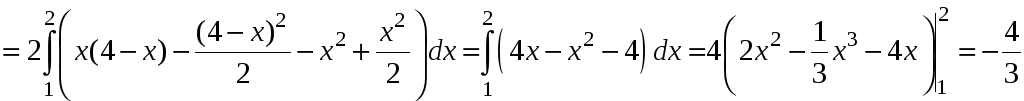II. Вычислим теперь непосредственно криволинейный интеграл по контуру (L), состоящему из звеньев (AB), (ВС), (СА):

.

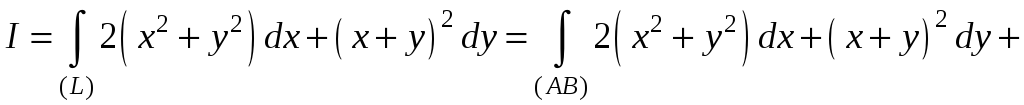
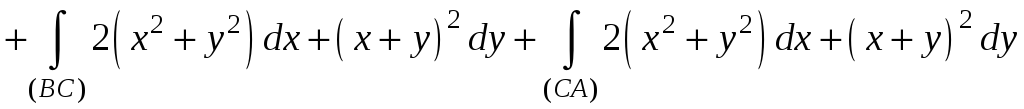Уравнение (AB): ; следовательно, изменяется от 1 до 2.

Уравнение (ВС): ; следовательно, изменяется от 2 до 1.

Уравнение (СА): ; значит, изменяется от 3 до 1. Тогда

.

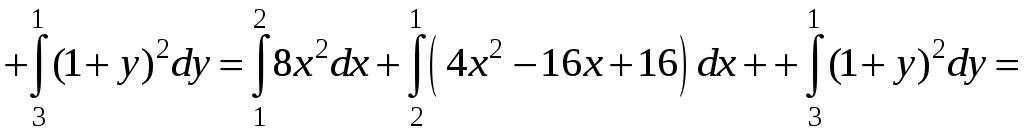
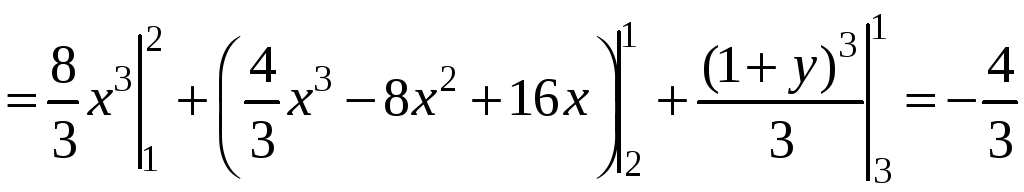Пример 2. Вычислить с помощью формулы Грина-Остроградского

,

где (L) – проходимый в положительном направлении замкнутый контур, состоящий из правой полуокружности и участка оси OY.

Решение. Приведем уравнение окружности к виду :

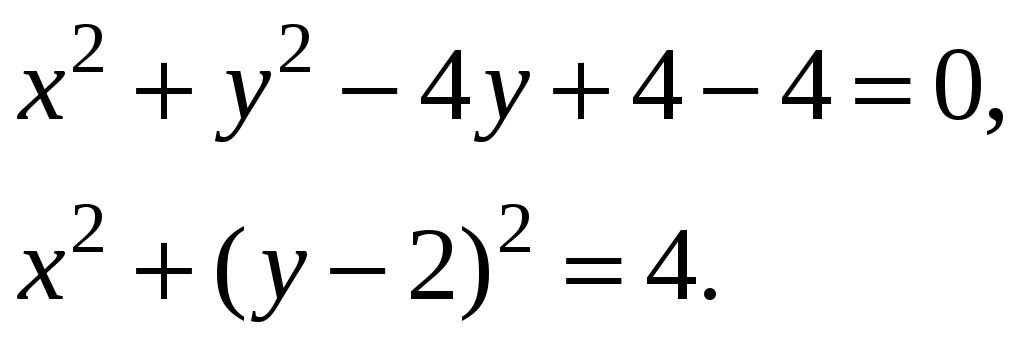
Следовательно, окружность имеет центр (0,2), радиус 2. Изобразим контур интегрирования OABO.

В рассматриваемом примере

,

.

Функции P(x,y) и Q(x,y) непрерывны вместе со своими частными производными и везде на R², следовательно, и на простой области (D), ограниченной контуром OABO. Тогда по формуле Грина-Остроградского получаем:

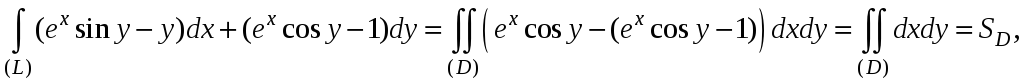где – площадь области (D).

В данном примере область (D) является полукругом радиуса 2, следовательно, .

Таким образом, .

Замечание 1. Формулу Грина-Остроградского можно непосредственно применять только к криволинейным интегралам по замкнутому контуру!

Замечание 2. С помощью формулы Грина-Остроградского криволинейный интеграл сводится к двойному интегралу, для нахождения которого может быть удобен переход к полярным координатам.

Пример 3. С помощью криволинейного интеграла вычислить площадь области (D), которая ограничена кривыми , .

Решение. Изобразим область (D) на рисунке. Найдем координаты точки В, как координаты точки пересечения кривых , .

Решая систему, составленную из уравнений этих кривых, получаем, что координаты точки В.

П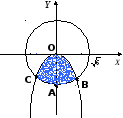лощадь плоской области (D) можно найти по формуле

,

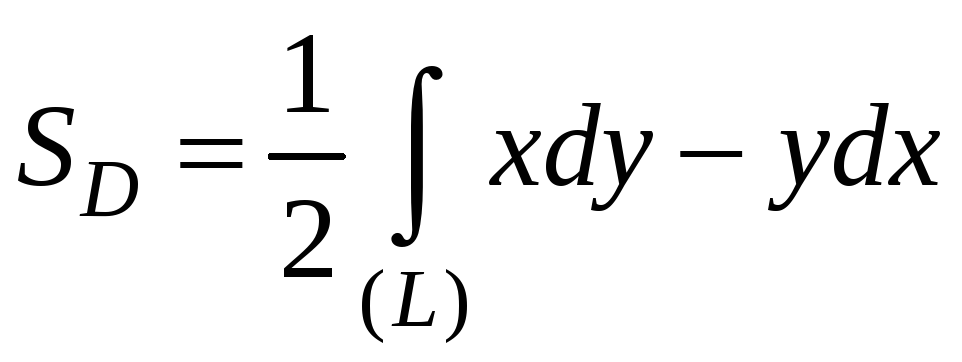где (L) – граница области (D), а интегрирование по контуру (L) ведется в положительном направлении.

В данной задаче область (D) ограничена контуром OCABO.

Так как область (D) симметрична относительно оси OY, то

,

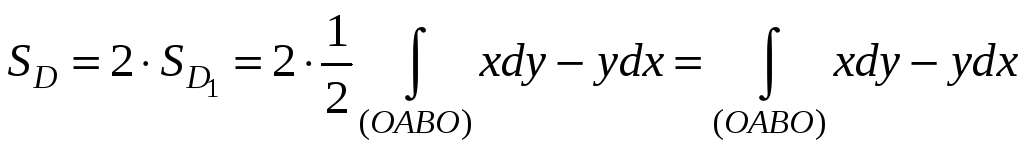где (D₁) – область, ограниченная контуром OABO.

Криволинейный интеграл обладает свойством аддитивности, поэтому

.

Рассматриваем каждый участок контура OABO отдельно.

1) OA: x=0, dx=0. Тогда .

2) AB: , 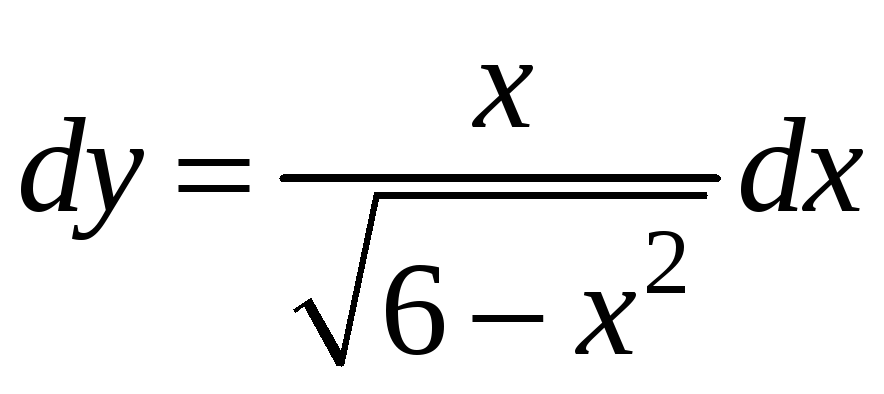. Тогда

.

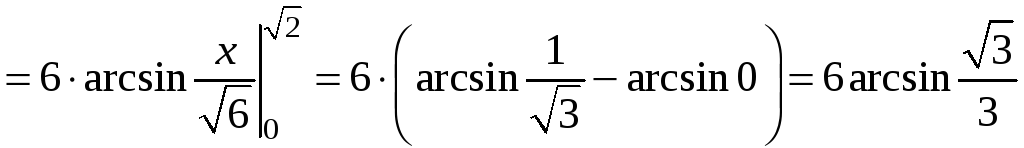3) BO: . Тогда

.

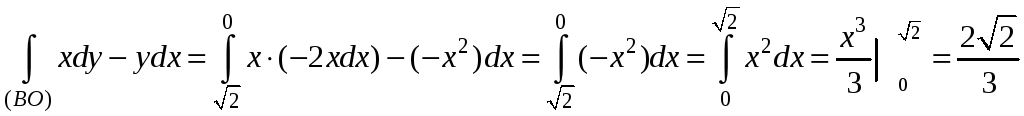Таким образом, .

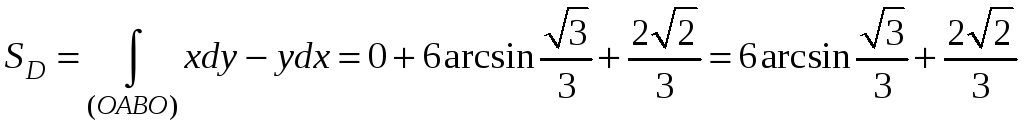Пример 4. Вычислить криволинейный интеграл, доказав его независимость от пути интегрирования: .

Решение. Докажем, что интеграл не зависит от пути интегрирования на некоторой области (D). Согласно теореме 2 пункта 5, если:

1) функции P(x,y), Q(x,y) непрерывны вместе со своими частными производными и на области (D);

2) на области (D);

3) область (D) является односвязной,

то криволинейный интеграл не зависит от пути интегрирования на области (D).

Выясним, на какой области выполняются условия 1)–3) для данного интеграла.

,

.

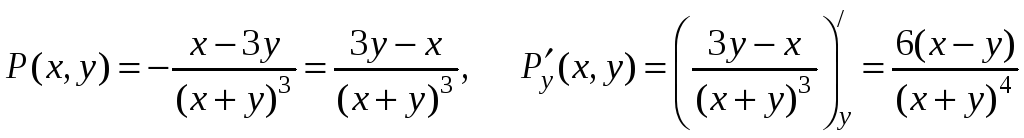У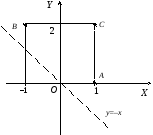словия 1), 2) выполняются на области , которая не является односвязной (эта область даже не является связной). Поэтому рассмотрим область , которая является односвязной, и в которой лежат точки А(1,0) и В(–1,2). На этой односвязной области (D) выполняются условие 1) и равенство , следовательно, данный интеграл не зависит от пути интегрирования на области (D).

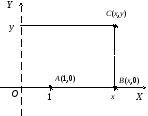
Чтобы вычислить интеграл, выберем путь АСВ (удобнее интегрировать по прямым, параллельным осям координат).

В силу аддитивности криволинейного интеграла имеем:

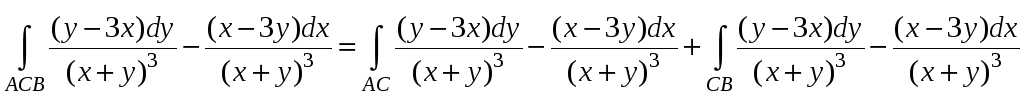
1) AC: x=1, dx=0. Тогда

.

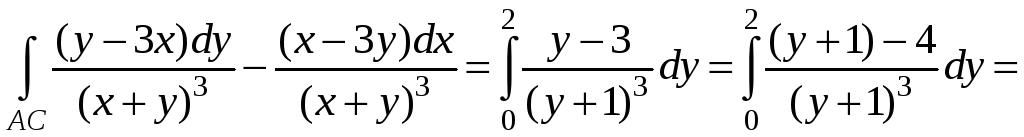
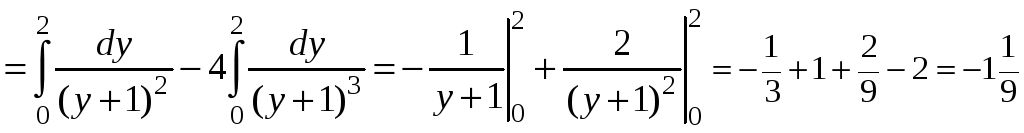2) CB: y=2, dy=0.

Тогда

.

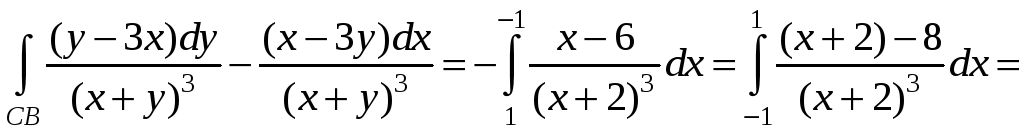
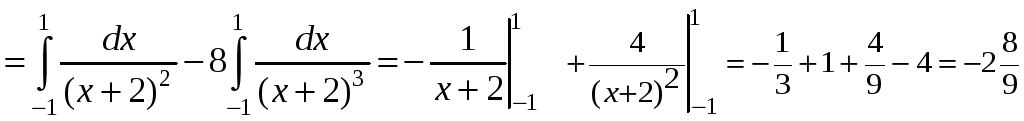Таким образом, .

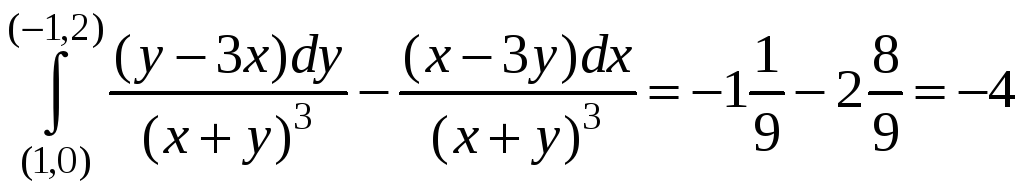Заметим, что данный криволинейный интеграл равен числу –4 по любому пути, соединяющему точки А(1,0) и В(–1,2) и лежащему в области .

Пример 5. Доказать, что дифференциальное выражение

является полным дифференциалом некоторой функции двух переменных, и найти все такие функции.

Решение. Согласно следствию (см. пункт 5), дифференциальное выражение является полным дифференциалом некоторой функции на области (D), если выполняются условия:

1) функции P(x,y), Q(x,y) непрерывны вместе со своими частными производными и на области (D);

2) на области (D);

3) область (D) является односвязной.

,

.

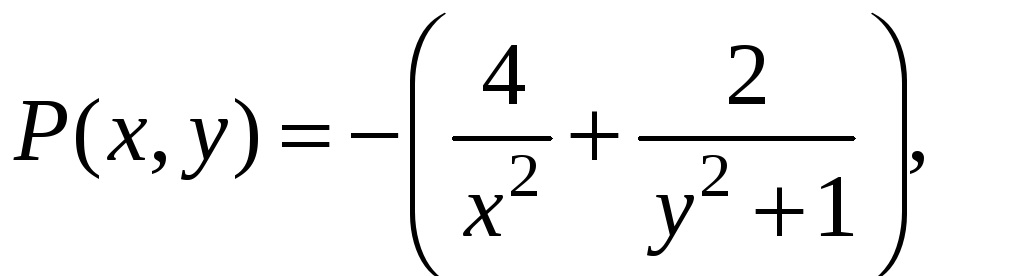
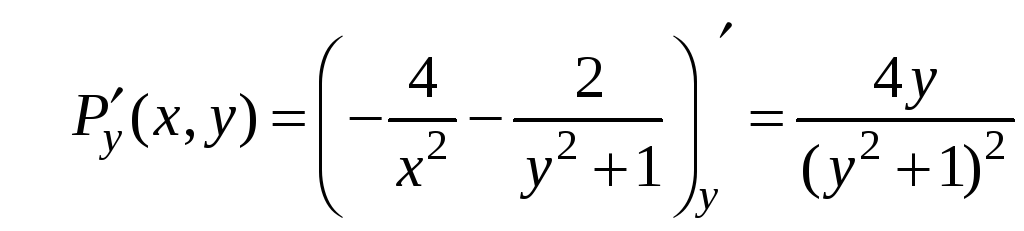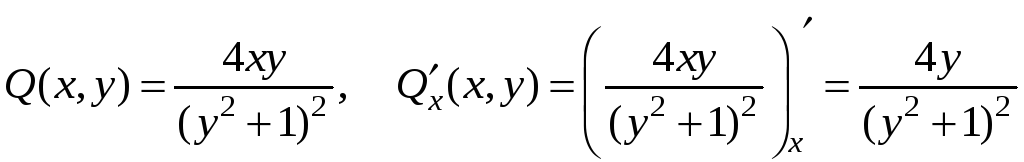Для данного дифференциального выражение условия 1)–2) выполняются на области , которая не является связной.

Поэтому рассмотрим область , которая является односвязной. На этой области (D) выполняются условия 1)–3), следовательно, существует функция F(x,y) такая, что полный дифференциал этой функции совпадает с данным дифференциальным выражением:

.

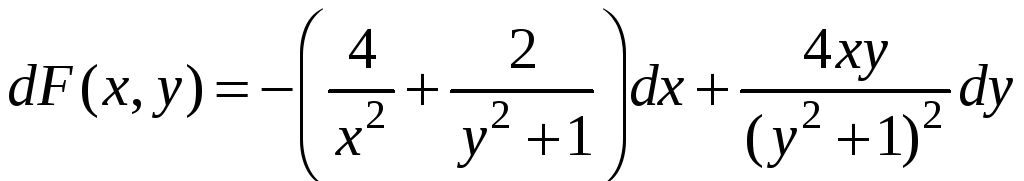Очевидно, что таких функций F(x,y) существует бесконечно много, друг от друга они отличаются на постоянную величину. Находим функцию F(x,y) по формуле: ,

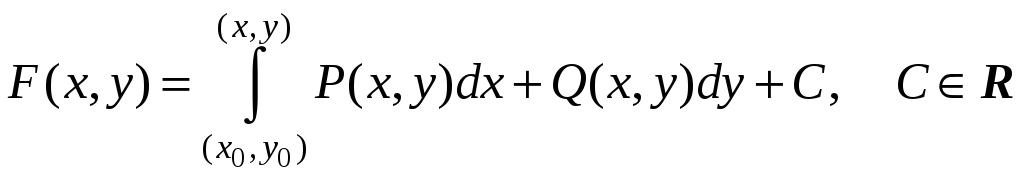где – произвольная фиксированная точка области (D).

Выберем точку =(1,0). В силу вышеизложенного интеграл

не зависит от пути интегрирования на области (D). Выбираем путь интегрирования ABC.

1) AB: y=0, dy=0.

.

2) BC: x=x=const, dx=0.

.

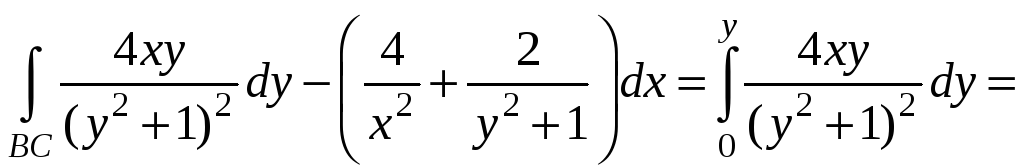
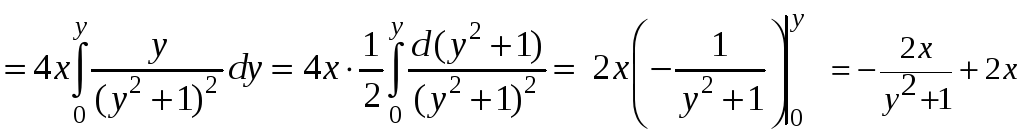Тогда .

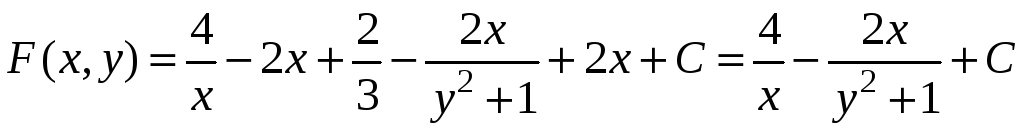Первообразная для данного дифференциального выражения найдена на области . Для области необходимо изменить начальную точку и все рассуждения провести аналогично. При этом в большинстве задач при нахождении первообразных дифференциального выражения на разных областях получаются одинаковые семейства первообразных.