2. Некоторые свойства криволинейного интеграла второго рода

Для краткости формулировок рассмотрим свойства криволинейного интеграла только для интеграла по переменной x, то есть для .

Свойство 1. Если функция f интегрируема вдоль кривой (АВ), , то функция также интегрируема вдоль кривой (АВ) и справедливо равенство:

.

Свойство 2. Если функции f и g интегрируемы вдоль кривой (АВ), то функция также интегрируема вдоль кривой (АВ) и справедливо равенство:

.

Свойство 3 (аддитивность). Если функция f интегрируема вдоль кривой (АВ), то функция f интегрируема вдоль кривых (АС) и (СВ) и справедливо равенство:

Свойство 4. Если функция f интегрируема вдоль кривой (АВ), то она интегрируема вдоль кривой (ВА) и справедливо равенство:

Свойство 5. Если функция f интегрируема по замкнутому контуру (L), то величина криволинейного интеграла не зависит от того, какую точку контура принять за начальную.

3. Существование и вычисление криволинейных интегралов второго рода

Теорема. Пусть кривая (L)=(AB) задана параметрическими уравнениями , где , - непрерывно дифференцируемые функции на , Пусть функции , P(x,y), Q(x,y) непрерывны на кривой (L). Тогда существуют интегралы , и справедливы равенства:

; ;

.

Замечание 1. Пусть кривая (АВ) задана явным уравнением , где функция непрерывно дифференцируема на отрезке [a,b], , . Тогда если функция f непрерывна на кривой (АВ), то справедлива формула: .

Замечание 2. Если кривая (АВ) представляет собой прямолинейный отрезок, параллельный оси OY, то .

(Это следует из того, что в интегральных суммах . Тогда и .)

Аналогично, если кривая (АВ) есть отрезок, параллельный оси OX, то .

4. Формула Грина-Остроградского

Формула Грина-Остроградского связывает двойной интеграл по области (P) с криволинейным интегралом по границе (L) этой области.

Область (P) называется простой, если она одновременно является простой областью I типа и II типа. Очевидно, что любая прямая, параллельная осям координат, пересекает простую область не более чем в двух точках.

Теорема. Пусть (P) простая область (или область, представимая в виде конечного числа простых областей), (L) - ее контур. Тогда если P(x,y), Q(x,y) непрерывны вместе со своими частными производными , на замкнутой области (P), то справедлива формула:

(3)

где интегрирование по контуру (L) ведётся в положительном направлении.

Формула (3) называется формулой Грина-Остроградского.

Из формулы Грина-Остроградского можно вывести формулу для вычисления площади плоской области (P) с границей (L):

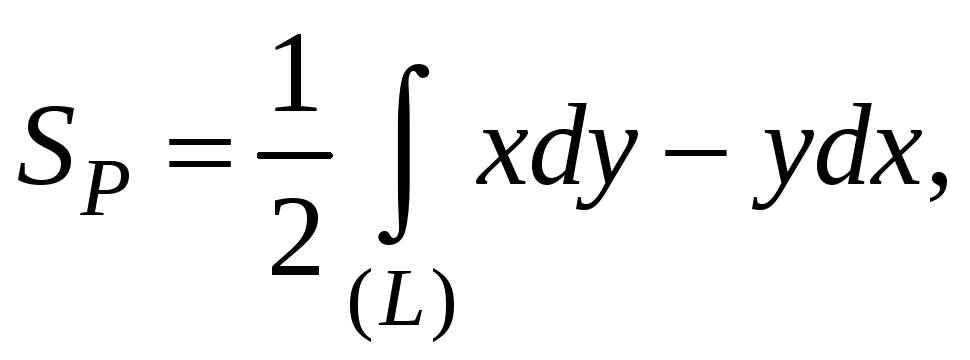
где интегрирование по контуру (L) ведётся в положительном направлении.

5. Криволинейные интегралы, не зависящие от пути интегрирования

Все рассматриваемые кривые предполагаются кусочно-гладкими.

Определение 1. Область называется связной, если любые две точки области можно соединить ломаной, целиком лежащей в этой области.

Определение 2. Связная область (D) называется односвязной, если любой замкнутый контур, лежащий в (D), ограничивает область, также целиком лежащую в (D). (Проще: односвязная область не имеет «дыр»).

Пусть на области (D) заданы две непрерывные функции P(x,y) и Q(x,y). Возьмем любые две точки и зафиксируем их. Соединим A и B всевозможными кривыми (L), лежащими в области (D). Тогда интеграл

(1)

будет иметь различные значения в зависимости от кривой (L).

Определение 3. Если для любых фиксированных точек значение криволинейного интеграла (1) по любой кривой, лежащей в области (D) и соединяющей точки A и B, одно и тоже, то говорят, что интеграл (1) не зависит от пути интегрирования на области (D). В этом случае значение интеграла (1) определяется только заданием точек A и B.

Условия независимости криволинейного интеграла от пути интегрирования на области (D) задаются следующими теоремами.

Теорема 1. Для того чтобы криволинейный интеграл (1) не зависел от пути интегрирования на области (D) необходимо и достаточно, чтобы он был равен нулю по любому замкнутому контуру, лежащем в области (D).

Теорема 2. Пусть функции P(x,y) и Q(x,y) непрерывны вместе со своими частными производными и на области (D). Для того чтобы криволинейный интеграл (1) на области (D) не зависел от пути интегрирования необходимо, а в случае односвязности области (D) и достаточно, чтобы во всех точках области (D) выполнялось равенство .

Теорема 3. Пусть функции P(x,y) и Q(x,y) непрерывны на области (D). Для того чтобы интеграл не зависел от пути интегрирования необходимо и достаточно, чтобы подынтегральное выражение являлось полным дифференциалом некоторой функции F(x,y), определенной на области (D), т.е.

.

Из теорем 2 и 3 существует важное следствие.

Следствие. Пусть на односвязной области (D) функции непрерывны. Для того чтобы на области (D) выражение было полным дифференциалом некоторой функции необходимо и достаточно, чтобы на области (D) выполнялось следующее условие .

Определение. Функция F(x,y) называется первообразной дифференциального выражения на области (D), если на этой области .

Если F(x,y) является первообразной выражения на области (D), то также является первообразной для выражения , то есть выражение имеет бесконечно много первообразных. Их общий вид .

В ходе доказательства теоремы 3 обосновывается, что одной из первообразных для выражения является функция

,

где - некоторая произвольная фиксированная точка области (D).

Тогда общий вид первообразных для выражения :

.

Заметим, что в этом равенстве интеграл не зависит от пути интегрирования на области (D).