
- •Глава1. Множества. Вещественные числа. Операции над множествами Множества. Вещественные числа. Операции над мнoжествами.
- •Сравнение множеств по числу элементов.
- •Счетные множества.
- •Счетность множества рациональных чисел.
- •Соответствие точка-число. Вещественные числа.
- •Множества мощности континуума
- •Супремум и инфимум числовых множеств.
- •Приближение вещественных чисел рациональными.
- •Терминология. Неравенства.
Счетность множества рациональных чисел.
Школьная математика имеет дело в основном с рациональными числами.
Рациональным числом называется число вида:
![]()
Что мы умеем делать с этими числами?
1) Складывать и вычитать:
Если![]() ,
то
,
то
![]()
2) Умножать и делить:
![]()
3) Сравнивать:
Если
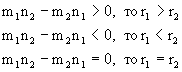
Но в связи с изучаемыми понятиями для нас нужна следующая теорема.
Теорема. Множество рациональных чисел счетно.
Доказательство.
Представим множество всех рациональных чисел в виде бесконечной таблицы.
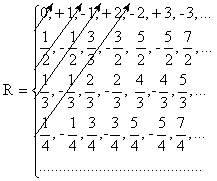
Оценим, как строятся строки этой таблицы.
Первая строка – это все целые числа, расположенные по возрастанию их модуля и так, что знаки “+” и “–” чередуются.
Вторая строка – это все несократимые дроби со знаменателем 2, расположенные по возрастанию их модуля и так, что знаки “+” и “–” чередуются.
Третья строка – это все несократимые дроби со знаменателем 3, расположенные по возрастанию их модуля и так, что знаки “+” и “–” чередуются.
Вообще,n-ая строка это все несократимые дроби со знаменателем n, расположенные по возрастанию их модуля и так, что знаки “+” и “–” чередуются.
Очевидно, что в этой таблице находятся все рациональные числа. Используя снова прием диагонализации представим R в виде:
![]()
Так как R представилось в форме последовательности, то отсюда следует, что R –счетное множество.
Соответствие точка-число. Вещественные числа.
Разберем сначала правило, которое каждой точке прямой линии ставит во взаимно-однозначное соответствие некоторое число
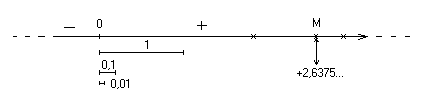
Пусть имеется некая бесконечная прямая. Проделаем следующее:
-
На этой прямой выберем какую-то точку, которую будем считать за начало отсчета. Этой точке поставим в соответствие число +0,0000…
-
Будем считать, что если точка расположена правее начала отсчета, то соответствующее ей число имеет знак +, а если левее – то знак –. Тем самым на прямой будет задано направление.
-
Выберем некоторый отрезок, длину которого будем считать за 1.
-
Пусть М – некоторая точка прямой, расположенная скажем, правее точки отсчета. Будем откладывать от начала отсчета единичные отрезки до тех пор, пока конец не “перескочит” точку М. Сколько раз этот единичный отрезок уложится до точки М определит нам целую часть числа, соответствующего этой точке (на рисунке +2).
-
Разделим отрезок, равный 1 на 10 равных частей, и от последней точки будем откладывать теперь этот отрезок, равный
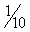 .
Сколько раз он уложился до точки М,
определит нам первую цифру числа после
запятой (на рисунке +2,6)
.
Сколько раз он уложился до точки М,
определит нам первую цифру числа после
запятой (на рисунке +2,6)
-
Разделим отрезок,равный
 снова
на 10 равных частей, и от последней точки
будем откладывать теперь этот отрезок,
равный
снова
на 10 равных частей, и от последней точки
будем откладывать теперь этот отрезок,
равный
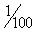 .
Сколько раз он уложился до точки М,
определит нам вторую цифру числа после
запятой (на рисунке +2,63)
.
Сколько раз он уложился до точки М,
определит нам вторую цифру числа после
запятой (на рисунке +2,63)
-
Разделим отрезок, равный
 снова
на 10 равных частей, и …
снова
на 10 равных частей, и …
Продолжая этот процесс деления отрезка на 10 равных частей неограниченное число раз, мы и получим число, соответствующее точке М нашей прямой (см. на рис. +2,6375…).
Сделаем
только одну важную оговорку. Что делать,
если на каком-то этапе конец отрезка
“воткнется” в точку М, т.е. совпадет с
ней? Здесь, конечно, дело вкуса. Для
определенности договоримся, что мы
всегда будем откладывать отрезок по
недостатку,
т.е. так, чтобы его конец не превосходил
точки М и не совпадал с ней. Поэтому,
скажем, точке М, расположенной на
расстоянии ½ длины единичного отрезка
будет соответствовать число +0,49999… а
не число +0,5000… Эта оговорка гарантирует
нам взаимную однозначность соответствия
точка![]() число.
число.
Итак, каждой точке взаимно однозначно поставлено в соответствие некая бесконечная десятичная дробь, называемая вещественным числом. Дадим точное определение этим числам.
Вещественным числом называется бесконечная десятичная дробь вида:
![]()
где
ЗНАК![]()
![]()
а все цифры ai после запятойпринадлежат множеству {0,1,2,3,4,5,6,7,8,9}
Оговорки:
-
Запрещаются числа вида:
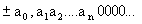
-
Существует особое число +0,0000…
Какое
же соотношение между рациональными и
вещественными числами?Конечно,каждое
рациональное число можно также можно
представить в виде бесконечной десятичной
дроби, т.е. рациональные числа входят
во все множество вещественных чисел.
Но эти дроби будит обязательно
периодическими.
Например,
![]() .
.
А если получающаяся дробь непериодическая, например такая +0,101001000100001…? Тогда она соответствует так называемому иррациональному числу.
Итак,{вещ.числа}={рац.числа}{иррац.числа}, где {рац. числа}- это периодические десятичные дроби, а {иррац. числа} это непериодические десятичные дроби.
Пусть даны два вещественных числа:
![]()
Будем считать, что a=b, если:
-
знак a = знак b
-
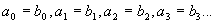
т.е. если у них одинаковые знаки и совпадают все соответствующие друг другу цифры.
