§ 4.3 Типы линейных операторов и их свойства

Рассмотрим основные типы линейных операторы и их матричные аналоги:

1. Оператор , действующий по правилу для любого элемента , называется нулевым оператором и ему соответствует нулевая матрица.

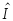2. Оператор , действующий по правилу  , называется тождественным (единичным) оператором и ему соответствует единичная матрица.

3. Оператор называется обратным к оператору , если и ему соответствует обратная к А матрица, обозначаемая А^-1.

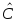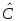4. Суммой = линейных операторов и называют оператор такой, что и оператору С соответствует сумма матриц А + В.

5. Произведением = линейных операторов и называется оператор , которому соответствует произведение матриц А,В: .

6. Операторы , будут равными, если равны их матрицы А и В.

7. Операторы можно умножать на некоторое число (или их матрицы

можно умножать на число).

Таким образом, для линейных операторов выполняются все свойства, свойственные матрицам, т.е. линейные операторы образуют линейное пространство.

Определение 1. Оператор называется сопряженным к линейному оператору , действующему в евклидовом пространстве , если для любых выполняется

.

Матрица А^Ж сопряженного оператора в ортонормированном базисе является транспонированной к А и сохраняет все свойства транспонированных матриц.

Пример. Рассмотрим вектора х =(2,3), y =(1,2) и матрицу оператора :А = . Тогда, х=Ах^т=(9,19)=z и (z,y)=47.

С другой стороны, :А^Т=,y=A^тy^т=(13,7)=f и (х,f)=47

Определение 2. Линейный оператор в евклидовом пространстве называется симметричным ( самосопряженным ), если x=х

В любом ортонормированном базисе матрица симметричного оператора является симметричной: и сохраняет все свойства симметричных матриц.

Пример. Рассмотрим вектор х =(2,3)и матрицу самосопряженного оператора :А = . Тогда, х^т=(8,13), х^т=(8,13)

§ 4.4 Операторы аффинных и ортогональных преобразований

В различных разделах математики приходится иметь дело с переменными х₁,х₂…,х_m, которые являются функциями других переменных y₁,y₂…,y_n,т.е.

х₁= f(y₁,y₂…,y_n)

х₂= f(y₁,y₂…,y_n)

……………………………………

х_m= f(y₁,y₂…,y_n)

Такого рода выражение одной системы переменных через другую называют преобразованием переменных. Если одна система переменных выражается через другую систему при помощи многочленов первой степени (линейных однородных функций первого порядка), то такие преобразования называют линейными, т.е

х₁= а₁₁y₁+ а₁₂y₂ + …+ а_1ny_n

х₂= а₂₁y₁+ а₂₂y₂ + …+ а_2ny_n ( 1 )

……………………………………

х_m= а_m1y₁+ а_m2y₂ + …+ а_mny_n

Матрица А, составленная из коэффициентов при переменных y₁,y₂…,y_n называется матрицей линейного преобразования. Очевидно, что в результате последовательно выполнения двух и более линейных преобразований переменных мы снова получаем линейное преобразование. Если первое преобразование характеризуется матрицей А, а второе - матрицей В, то в результате последовательного выполнения двух преобразований получим новое, определяемое матрицей С = АВ. Понятно, что при этом должны соблюдаться требования, принятые для произведений двух матриц.

Если количество переменных одинаково и матрица преобразований от Х к Y неособенная, то определено обратное линейное преобразование от Y к Х.

Переходя от переменных x, y к их векторной записи, систему (1) можно записать в виде: Х = АY, где X,Y – вектора – столбцы, а матрица А может считаться матрицей линейного оператора в векторном пространстве Rⁿ.

Определение 1. Если определитель квадратной матрицы А оператора не равен нулю, то линейное преобразование, осуществляемое по данному оператору, называют неособенным линейным преобразованием.

Пример.

Рассмотрим вектора в R²: а = (1,1), b =(3, -3), c =(2, 0) и неособенную матрицу линейного преобразования . Применяя ее к каждому из векторов, получим вектора Аа^т=, Аb^т=, Аc^т=, т.е. в результате данного преобразования треугольник переходит в треугольник. Легко проверить, что при этом величины углов, площадей, длины отрезков и т.д. не сохраняются (смотри рисунок).

3

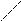
2

1

-1 1 2 3

-2

-3

Таким образом, неособенное линейное преобразования сохраняя типы

фигур (многоугольники в многоугольники), не сохраняют метрику. В литературе такие преобразования иногда называют аффинными.

Определение 2. Линейный оператор , действующий в евклидовом пространстве, называется ортонормированным, если для любых из этого пространства выполняется равенство

(2).

Линейное преобразование, осуществленное по данному оператору, называют линейным ортонормированным преобразованием.

Замечание. Условие (2) означает, что ортонормированный оператор сохраняет скалярное произведение и те величины, которые выражаются

через скалярное произведение – длину векторов и угол между векторами. Ортонормированный оператор в Rⁿ производит поворот пространства вокруг начала координат, оставляя начало координат неподвижным.

Теорема. Если - ортонормированный линейный оператор, заданный в евклидовом пространстве и ортонормированный базис, то матрица А = {a_ij} ортонормированного оператора обладает свойством

(i  j ) (3)

Обратно, любая матрица А, удовлетворяющая условию (3), является матрицей некоторого ортонормированного линейного оператора

Пример.

Применим к векторам а = (1,1), b =(3, -3), c =(2, 0) из предыдущего примера ортонормированный оператор с ортонормированной матрице

.

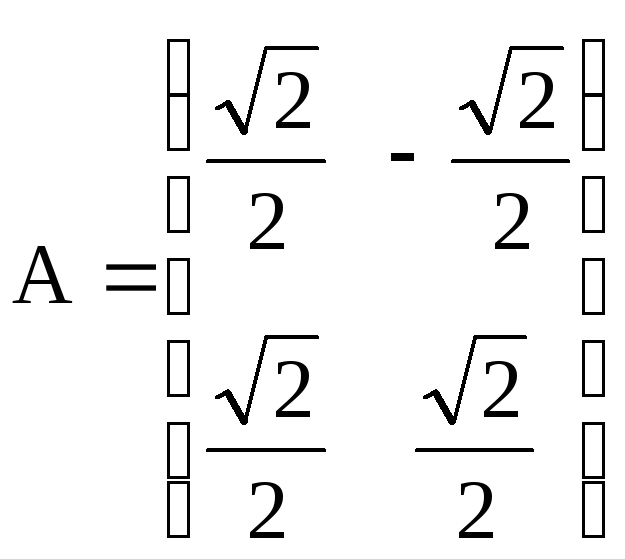Результатом применения оператора А будут вектора:

Аа^т = , Аb^т = , Аc^т =

или в геометрическом представлении произойдет поворот треугольника вокруг центра с сохранением длин, углов и площадей.

3

2

1

-1 1 2 3

-2

-3

Используя свойства векторного произведения легко найти площади двух треугольников:

S₁ = 0.5= 1, S₁ = 0.5= 1

Определение 3. Оператор - ортогональный линейный оператор, заданный в евклидовом пространстве с базисом тогда и только тогда, когда матрица А = {a_ij} оператора обладает свойством

(i  j ) (4)

Пример.

Применим к векторам а = (1,1), b =(3, -3), c =(2, 0) из предыдущих примеров ортогональный оператор с ортогональной матрицей

Результатом применения оператора А будут вектора:

Аа^т = , Аb^т = , Аc^т =

или в геометрическом представлении произойдет поворот треугольника без сохранения длин, углов и площадей.

3

2

1

-1 1 2 3

-2

-3

Площади двух треугольников: S₁ = 0.5= 1, S₁ = 0.5= 2

Заметим, что площади двух треугольников ортогональной матрицы А.

отличаются на константу , т.е. а₁₁² + а₂₁² = 2.

Основные свойства линейных ортонормированных (ортогональных) и аффинных преобразований :

1. Ортонормированное (ортогональное) преобразование – частный случай аффинного преобразования.

2. Ортонормированные преобразования сохраняют расстояние, углы и площади, а ортогональное преобразование меняет расстояние, углы и площади на величину .

3. Аффинные и ортонормированные (ортогональные) преобразования обратимы, тождественны и транзитивны

4. Аффинные преобразования не сохраняют метрики, но сохраняют тип фигуры.