
- •Глава 4 Теория линейных операторов
- •§ 4.1 Линейные операторы в конечномерных пространствах
- •§ 4.2 Основные теоремы о линейных операторах
- •§ 4.3 Типы линейных операторов и их свойства
- •§ 4.4 Операторы аффинных и ортогональных преобразований
- •§ 4.5 Собственные вектора и собственные значения самосопряженных операторов
Глава 4 Теория линейных операторов
§ 4.1 Линейные операторы в конечномерных пространствах
Определение
1.
Линейным
оператором
![]() ,
действующим в n-мерном
координатном евклидовом
пространстве
,
действующим в n-мерном
координатном евклидовом
пространстве
![]() над полем К, называется такое отображение
, что
над полем К, называется такое отображение
, что
-
Область определения
 есть
пространство
есть
пространство
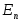
-
Множество значений
 принадлежит
пространству
принадлежит
пространству
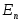
(иными
словами, каждому вектору
![]() ставится в соответствие определенный
вектор
ставится в соответствие определенный
вектор
![]()
-
Для любых векторов
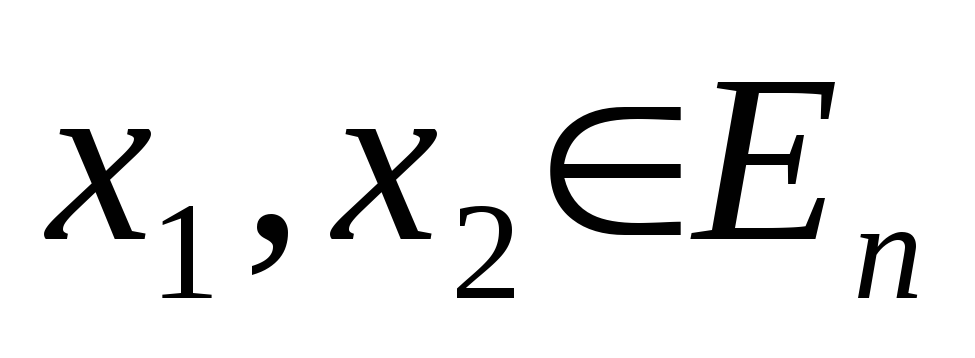 и любого числа
и любого числа
 из поля К выполняются равенства:
из поля К выполняются равенства:
![]() (аддитивное
свойство);
(аддитивное
свойство);
![]() (свойство
однородности).
(свойство
однородности).
При
этом используют следующую терминологию:
вектор
![]() называют образом
вектора
называют образом
вектора
![]() при данном отображении
при данном отображении
![]() (или результатом действия линейного
оператора
(или результатом действия линейного
оператора
![]() на вектор
на вектор
![]() ),
вектор
),
вектор
![]() называют прообразом
вектора
называют прообразом
вектора
![]() .
.
Фактически
линейный
оператор
можно рассматривать, как векторную
функцию,
заданную на пространстве
![]() со значениями в
со значениями в
![]() (сама
в себя).
Оператор называется линейным потому,
что в силу свойств аддитивности и
однородности линейно зависимые вектора
под действием этого оператора переходят
в также линейно зависимые вектора.
Очевидно, что нулевой вектор переходит
в нулевой.
(сама
в себя).
Оператор называется линейным потому,
что в силу свойств аддитивности и
однородности линейно зависимые вектора
под действием этого оператора переходят
в также линейно зависимые вектора.
Очевидно, что нулевой вектор переходит
в нулевой.
Из сказанного выше следует, что под действием линейного оператора прямые переходят в прямые, параллельные в параллельные, плоскости в плоскости и т.д. При этом длины отрезков, величины углов, вообще говоря, не сохраняются.
Примерами линейных операторов в R2 являются: поворот вокруг начала координат, растяжение или сжатие в направлении какой-либо прямой, проходящей через начало координат и т.д.
Механизмом,
реализующим действие линейного оператора
![]() ,
является его матричное
представление.
,
является его матричное
представление.
Пусть
в пространстве
![]() фиксирован некоторый базис
фиксирован некоторый базис
![]() .
Возьмем произвольный вектор
.
Возьмем произвольный вектор
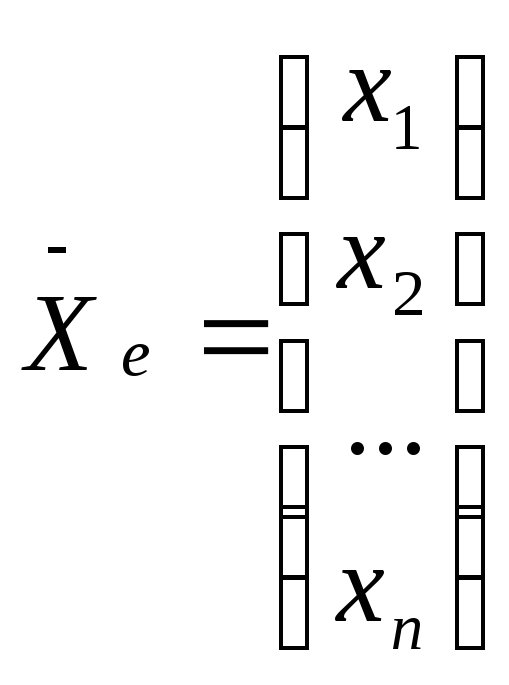
![]()
и его
разложение
![]() базису Е.
базису Е.
Рассмотрим
действие оператора
![]() по отношению к векторам
по отношению к векторам
![]() .
.
Разложение
вектора
![]() по базису
по базису
![]() имеет вид:
имеет вид:
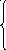 f1=
f1=![]() ,
,
f2=![]() ,
(1)
,
(1)
. . . . . . . . . . . .
fn=![]() .
.
Определение
2.
Матрицей
линейного оператора
![]() в базисе Е
называют
квадратную матрицу (n
x
n)
в базисе Е
называют
квадратную матрицу (n
x
n)

в k-ом
столбе которой записаны коэффициенты
разложения
![]() по базису Е.
по базису Е.
Иными
словами, под воздействием оператора
![]() базисный
вектор переходит в новый вектор, причем
коэффициенты
разложения этого нового вектора
по базису Е
являются столбцами
матрицы линейного оператора.
Равенство (1) переводит векторы Е,
составляющие базис пространства, в
систему векторов F,
причем полученные вектора остаются в
исходном базисе Е. Эту операцию можно
записать в матричном виде
базисный
вектор переходит в новый вектор, причем
коэффициенты
разложения этого нового вектора
по базису Е
являются столбцами
матрицы линейного оператора.
Равенство (1) переводит векторы Е,
составляющие базис пространства, в
систему векторов F,
причем полученные вектора остаются в
исходном базисе Е. Эту операцию можно
записать в матричном виде
F=![]() или
или
![]() ,
,
где
![]()
![]() = F
-
матрица-строка, состоящая из образов
базисных векторов E.
= F
-
матрица-строка, состоящая из образов
базисных векторов E.
§ 4.2 Основные теоремы о линейных операторах
Теорема
1.
Если
определитель матрицы линейного оператора
![]() отличен от нуля, то система векторов
F=
отличен от нуля, то система векторов
F=![]() будет новым базисом в евклидовом
пространстве, порождаемым оператором
будет новым базисом в евклидовом
пространстве, порождаемым оператором
![]() .
.
Доказательство следует из свойств линейно независимых систем и определения базиса.
Пусть
в пространстве
![]() даны два произвольных базиса
даны два произвольных базиса
![]() и
и
![]() .
Используя полученные выше результаты,
разложим элементы 2-го базиса по 1-ому:
.
Используя полученные выше результаты,
разложим элементы 2-го базиса по 1-ому:

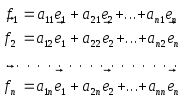 или
в матричной форме
или
в матричной форме
![]() .
.
Матрицу
![]() оператора
оператора
![]() будем называть
базисной
матрицей (матрица
перехода от первого базиса
будем называть
базисной
матрицей (матрица
перехода от первого базиса
![]() ко второму базису
ко второму базису
![]() ).
Принято использовать обозначение
).
Принято использовать обозначение
![]() .
.
Разложим
любой вектор
![]() по выбранным базисам :
по выбранным базисам :
![]() (1),
(1),
где
![]() и
и
![]() - вектор-столбцы координат данного
вектора
- вектор-столбцы координат данного
вектора
![]() в первом и во втором базисах соответственно.
Так как определитель базисной матрицы
отличен от нуля, то справедливы формулы
(проверяется подстановкой в (1)
в первом и во втором базисах соответственно.
Так как определитель базисной матрицы
отличен от нуля, то справедливы формулы
(проверяется подстановкой в (1)
![]() )
)

![]() (2),
(2),
которые называются формулами преобразования координат вектора при преобразовании базиса ( при переходе от старого к новому базису).
Пример.
-
Пусть
 -
базис в Е3
и заданы векторы
-
базис в Е3
и заданы векторы
 .
Доказать, что вектора
.
Доказать, что вектора
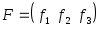 образует базис и найти разложение
вектора
образует базис и найти разложение
вектора
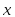 по этому базису.
по этому базису.
Решение.
Матрица
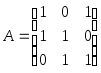 ,
составленная из столбцов координат
векторов
,
составленная из столбцов координат
векторов
![]() в базисе
в базисе
![]() ,
является невырожденной, и, следовательно,
векторы
,
является невырожденной, и, следовательно,
векторы
![]() являются линейно независимыми и также
образуют базис. При этом матрица
являются линейно независимыми и также
образуют базис. При этом матрица
![]() является матрицей перехода от базиса
является матрицей перехода от базиса
![]() к базису
к базису
![]()
 .
.
По формуле
(2)
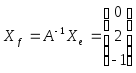 ,
то искомое разложение
,
то искомое разложение
![]() .
.
Теорема
2.
Если переход от базиса
![]() к базису
к базису
![]() ,
осуществляется по формуле
,
осуществляется по формуле
![]() ,
где
,
где![]() - базисная
матрица,
то матрицы операторов
- базисная
матрица,
то матрицы операторов
![]() e
и
e
и
![]() f
в базисах E
и
F
находят по формулам:
f
в базисах E
и
F
находят по формулам:
![]() или
или
![]() (3).
(3).
Доказательство. Теорема имеет наглядный геометрический смысл. Рассмотрим два базиса E и F в R2



 Yf
Yf
 Xe
Ae
Xe
Ae
Pef
 Ye
Ye


Система с базисом E Система с базисом F
Последовательность действий можно записать равенствами:
АeXe = Ye, Pef(Ye)= Yf или Pef(Ae)=Yf
С другой стороны, последовательность операций можно поменять
Xf


 Xe
Xe
Af

Pef Yf


Система с базисом е Система с базисом f
или
PefXe = Xf, АfXf = Yf или Аf(Pef) = Yf
и приравнивая левые части двух операций, получим требуемое:
PefAe
=
АfPef
или
![]() и
и
![]() .
.
где Р-1
-
базисная
матрица Pfe
при
переходе от базису
![]() к базису
к базису
![]() (является обратной к Pef).
(является обратной к Pef).
Пример.
1.Задан
оператор
![]() е
с
матрицей
е
с
матрицей
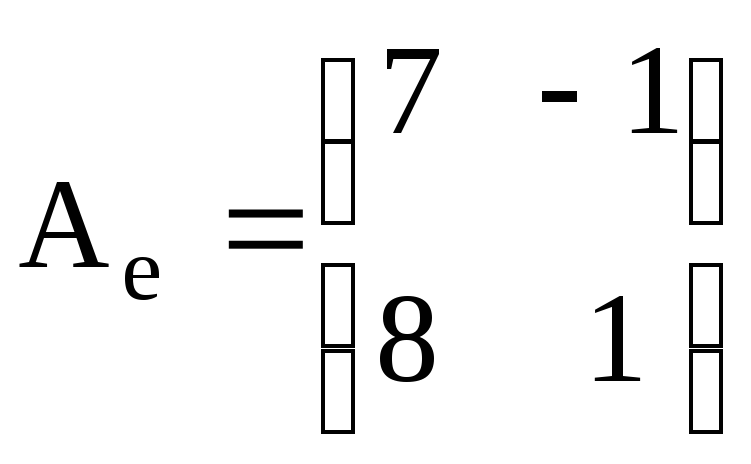 и матрица перехода
и матрица перехода
 от базиса
от базиса
![]() к базису
к базису
![]() .
Вычислить матрицу оператора
.
Вычислить матрицу оператора
![]() и найти образ
и найти образ
![]() вектора
вектора
 в базисе
в базисе
![]() двумя способами.
двумя способами.
Решение.
Находим
матрицу, обратную к Р:
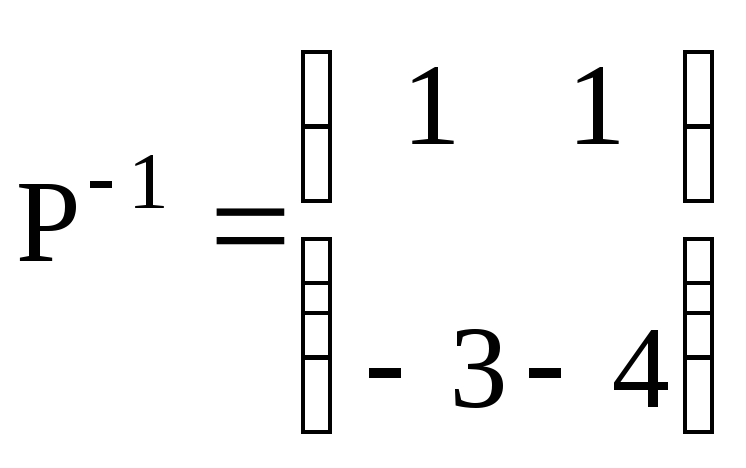 .
Находим матрицу оператора
.
Находим матрицу оператора
![]() :
:
![]() =
=
 .
.
Тогда
![]() =
=![]() =
=![]() и Рef(
и Рef(![]() )
=
)
=
![]() =
=
![]() .
.
С другой
стороны,
Рef(![]() =
=![]() =
=![]() и
и
![]()
![]() =
=
![]() .
.
