§ 1.8 Взаимная и обратная матрица

Определение 1. Квадратная матрица называется невырожденной ( или неособенной), если , в противном случае матрица называется вырожденной ( особенной ).

Определение 2. Пусть задана квадратная матрица А, то матрица называется взаимной к матрице , если в ее к-ой строке стоят алгебраические дополнения элементов k- го столбца матрицы А, т.е.

.

Теорема 1. Для взаимной матрицы квадратной матрицы А выполнено равенство

А=А = АI = АI = 

где  - определитель матрицы А.

Доказательство. Докажем для случая А = АI =  I

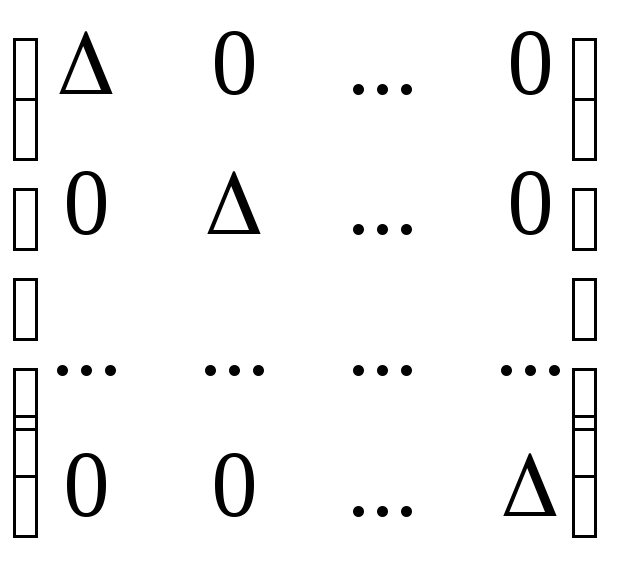А= = =  I

Теорема 2. Особенные матрицы обратных матриц не имеют. Всякая неособенная матрица имеет обратную и причем единственную, определяемую по формуле

Доказательство. По определению обратной Х матрицы А А^-1 = А^-1 А = I и свойству, что определитель произведение равен произведению определителей, получаем

А А^-1  =  А^-1  А = I= 1  0

т.е. определители матрицы А и А^-1 не равны нулю.

Используем теорему 1: если А =  I, то умножая слева на А^-1 получим А^-1А = А^-1 I или = А^-1 и окончательно будет

Докажем единственность. Пусть существуют 2 обратные матрицы Y₁, Y. Тогда А Y = I, Y₁ (А Y) = Y₁I, (Y₁ А)Y = Y₁ , I Y = Y₁, Y = Y₁

Следствие

1.. Свойство вытекает из цепочки равенств

2. Замечание:.

Показать, что если матрица А симметрическая (кососимметричная), то взаимная матрица А^ж также симметрическая (кососимметричная).

Пример. Найти обратную матрицу для матрицы .

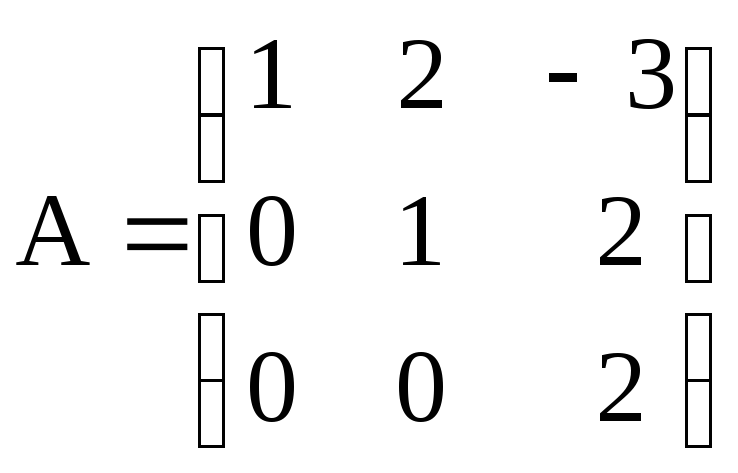Так как , то обратная матрица существует. Для удобства вычисления запишем транспонированную с ней матрицу

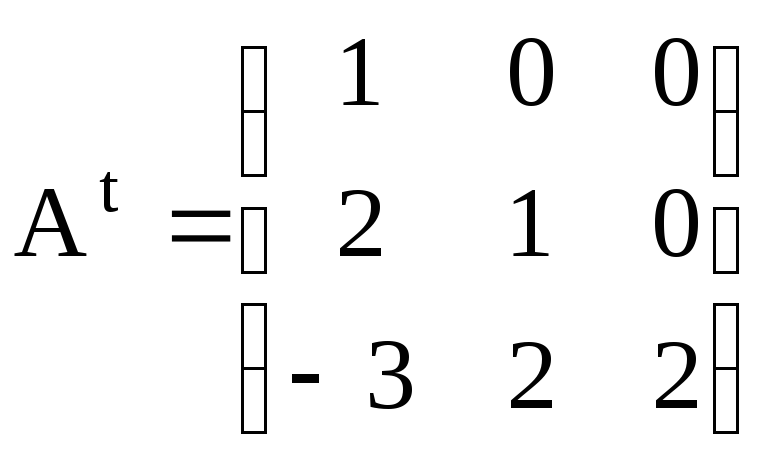, и найдем ее алгебраические дополнения

А₁₁ = 2, А₁₂ = 0, А₁₃ = 0,

А₂₁ =-4, А₂₂ = 2, А₂₃ = 0,

А₃₁ = 7, А₃₂ = -2, А₃₃ = 1

Взаимная матрица , обратная .