
- •Глава 1 Матрицы и определители
- •§ 1.1. Матрицы и их основные виды
- •§ 1.2. Линейное пространство
- •§ 1.3 Элементарные операции над матрицами
- •§ 1.4 Произведение матриц
- •Примеры: 1) .
- •§ 1.5 Специальные матрицы и их свойства
- •§ 1.6 Определитель n-го порядка
- •§ 1.7 Свойства определителей
- •§ 1.8 Взаимная и обратная матрица
§ 1.7 Свойства определителей
Свойство
1.
При
транспонировании матрицы ее определитель
не меняется, то есть
![]() .
.
Из определения определителя
![]()
и свойства транспонированной матрицы аij= atji, получаем
![]() =
detA
=
detA
Замечание. Данное свойство означает равноправие строк и столбцов определителя. Все дальнейшие свойства формулируются только для столбцов, подразумевая при этом, что они справедливы и для строк.
Свойство 2. Если один из столбцов матрицы состоит целиком из нулей, то ее определитель равен нулю.
Так в каждое слагаемое определителя входит по одному представителю из каждой строки, то в каждом слагаемом содержится по одному нулевому сомножителю, т.е.все слагаемые равны нулю.
Свойство 3. При перестановке двух столбцов матрицы ее определитель меняет знак
Пусть исходная матрица А, а ее определитель detA. Если поменять местами два столбца i и j, то получим матрицу В с определителем detB. Причем, в каждом слагаемом сомножитель, входивший в определитель матрицы А из i-го столбца, в определитель матрицы В войдет под номером j-го столбца и обратно. Согласно свойству транспозиций, при перемене двух индексов местами, каждая четная перестановка в detA станет нечетной в detB, а нечетная – четной, т.е. все слагаемые detA будут отличаться от слагаемых detB только знаками. Следовательно, detB = - detA.
Свойство 4. Если определитель имеет две одинаковых строки, то он равен нулю.
Пусть дана матрица А с определителем detA. Поменяв в матрице А две строки местами, получим аналогичную матрицу А, но ее определитель (по св.3)поменяет знак, т.е. detA = -detA или, что то же самое, 2detA = 0, тогда detA = 0.
Свойство 5. Перед формулировкой данного свойства необходимо ввести ряд новых определений и доказать несколько результатов.
Определение 1. Пусть задана матрица А. Вычеркнем из нее i-ю строку и k-ый столбец и не меняя порядка сомкнем строки и столбцы. Определитель вновь построенной матрицы А называют минором элемента aij матрицы А и обозначают ij.
Пример. Найти минор 23 элемента а23 матрицы А

 Из
матрицы А=
Из
матрицы А=
 вычеркиваем 2-ю строку и 3-ий столбец.
вычеркиваем 2-ю строку и 3-ий столбец.
Получаем
матрицу 23=![]() ,
ее определитель det
23=
3, то есть минор
элемента a23
матрицы А равен 3.
,
ее определитель det
23=
3, то есть минор
элемента a23
матрицы А равен 3.
Лемма. Пусть дана матрица А с первой строкой, содержащей один ненулевой элемент, т.е. матрица вида
А= ,то
определитель такой матрицы равен
detA=a11
11
,то
определитель такой матрицы равен
detA=a11
11
Доказательство. Рассмотрим определитель матрицы А
![]() (1)
(1)
Так как все элементы 1-ой строки, кроме первого, равны нулю, то формула (1) трансформируется в формулу
![]() =
а11
11
=
а11
11
где 11 – определитель матрицы, полученной из матрицы А удалением первой строки и первого столбца ( или минор элемента а11).
Теорема Пусть дана матрица с i-ой строкой, содержащей в k-ом столбце отличный от нуля элемент
А
=
 ,
,
то определитель матрицы А равен detA =(-1)i+k aik ik
Доказательство. Меняя i-ю строку с 1-ой строкой, мы совершим (i-1) перестановку строк, т.е. по свойству 3 произойдет (i-1) перемена знака. Поменяв k-ый столбец с 1-ым, мы совершим еще (k – 1) перемену знака и в результате придем к матрице, рассмотренной в лемме. Используя ее результаты, получаем detA =(-1)i+k aik ik
Определение 2. Выражение Аij =(-1)i+k ik называется алгебраическим дополнением элемента aij матрицы А.
Иначе: алгебраическим дополнением - это минор со знаком.
Заметим,
что алгебраическое дополнение
![]() не зависит как от элементов i-ой
строки, так и элементов j-ого
столбца, так как определяющий его минор
содержит элементы, не входящие в эти
стоки и столбцы.
не зависит как от элементов i-ой
строки, так и элементов j-ого
столбца, так как определяющий его минор
содержит элементы, не входящие в эти
стоки и столбцы.
Теперь можно сформулировать само свойство 5. Заметим, что в математической литературе это свойство часто фигурирует, как определение определителя.
Свойство 5. Определитель матрицы А равен произведению элементов произвольной строки (столбца) на свои алгебраические дополнения
![]() (2)
(2)
Формула (2) называется разложением определителя по i-ой строке.
Результат иллюстрируется на примере определителя 3-го порядка.
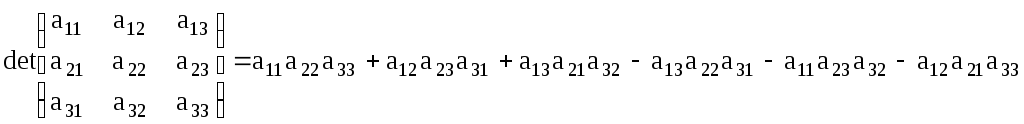
![]() а21А21+а22А22+а23А23
а21А21+а22А22+а23А23
Используя свойство 5, легко доказываются утверждения (доказать):
-
Определитель диагональной матрицы равен произведению элементов главной диагонали
-
Определитель треугольной матрицы равен произведению элементов главной диагонали
-
Определитель произведения двух матриц равен произведению определителей этих матриц, т.е. А В = А В
Пример
.

Свойство 6. Сумма произведений элементов какого-либо столбца на соответствующие алгебраические дополнения другого столбца равна нулю (принимаем без доказательства). Проверить на числовом примере
Свойство 7. Если элементы некоторой строки матрицы А умножить на любое число, то определитель полученной матрицы В будет отличаться от определителя исходной матрицы А на это число.
Доказательство.
Пусть
дана матрица А, где
![]() .
.
Умножив i-ю строку матрицы А на число r, получим новую матрицу В с определителем, определяемым свойством 5 :
![]() =
=
![]()
Следствия:
1.Общий множитель элементов одной строки можно выносить за знак определителя.
2.Если в матрице существуют 2 пропорциональные строки, то ее определитель равен 0 (коэффициент пропорциональности можно вынести за знак определителя, тогда матрица полученного определителя будет содержать две равные строки)
Свойство
8.
Если в матрице
![]() каждый элемент k-ого
столбца может быть представлен в виде
сумма двух слагаемых aik
=
bik
+ cik,
то определитель такой матрицы А представим
в виде суммы двух
определителей,
в первом
из которых на месте элементов k-го
столбца стоят элементы bik,
а во втором
определителе на месте элементов k-го
столбца стоят cik
(остальные элементы матрицы не меняются).
каждый элемент k-ого
столбца может быть представлен в виде
сумма двух слагаемых aik
=
bik
+ cik,
то определитель такой матрицы А представим
в виде суммы двух
определителей,
в первом
из которых на месте элементов k-го
столбца стоят элементы bik,
а во втором
определителе на месте элементов k-го
столбца стоят cik
(остальные элементы матрицы не меняются).
Доказательство. Воспользуемся свойством 5.
![]() =
=![]()
![]() detB
+ detC
detB
+ detC
Пример.
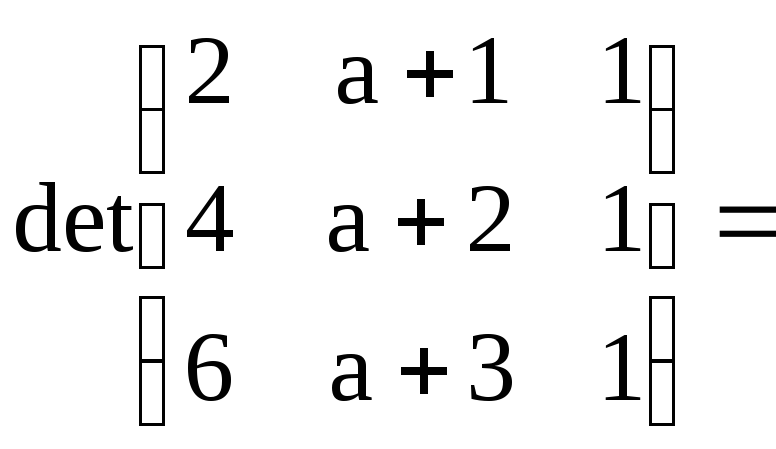

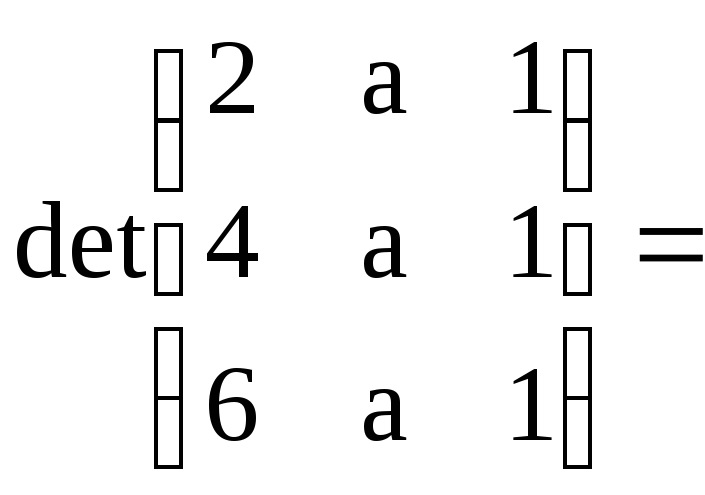 0
+ 0 = 0
0
+ 0 = 0
Свойство 9 Если к строке определителя прибавить любую другую его строку, умноженную на некоторое число k, то определитель не изменится.
Доказательство.
Пусть дана матрица А, где
![]() .
.
Умножив j-ю строку матрицы А на число r и прибавит эту строку к элементам i-ой строки получим новую матрицу А1 с определителем:
![]() =
=![]() =
0 + detA
=
0 + detA
Первый определитель равен нулю, т.к. в нем находятся две пропорциональные строки.
Пример. Вычислить определитель матрицы D четвертого порядка:
Умножим последовательно первую строку на (-2),(-5) и (-6) и прибавим ее соответственно ко второй, третьей и четвертой строке. По свойству 9 значение полученного определителя не изменится.


Теперь последовательно умножим 2-ю строку на 13 и 4 и прибавим ее к 3-ей и 4-ой строке. Получим определитель:

![]()
Свойство 10 Если один из столбцов матрицы А есть линейная комбинация других столбцов этой матрицы, то определитель такой матрицы равен нулю.
Доказательство. Пусть таким столбцом в матрице А является k- ый. Тогда, обозначив столбцы как А1,А2,…,Аk,…,Аn запишем линейную комбинацию для столбца k:
Аk = 1A1+ 2A2+ … + k-1Ak-1+ k+1Ak+1+…+nAn
Если вместо элементов k-го столбца в исходной матрице А записать данную комбинацию, то используя свойство 7 определитель матрицы А можно представить в виде (k – 1) определителя, в каждом из которых будут два пропорциональных столбца. Тогда, каждый из таких определителей равен нулю ( следствие 2 из свойства 7).
Свойство 11. Перед его формулировкой введем определение.
Определение.
Матрица вида
![]() ,
где А, В, С квадратные матрицы, называется
ступенчатой
матрицей.
,
где А, В, С квадратные матрицы, называется
ступенчатой
матрицей.
Определитель ступенчатой матрицы равен произведению определителей диагональных клеток.
Пример.
 =
=
![]()
![]() =
1 – 1 = 0.
=
1 – 1 = 0.
