
- •Глава 1 Матрицы и определители
- •§ 1.1. Матрицы и их основные виды
- •§ 1.2. Линейное пространство
- •§ 1.3 Элементарные операции над матрицами
- •§ 1.4 Произведение матриц
- •Примеры: 1) .
- •§ 1.5 Специальные матрицы и их свойства
- •§ 1.6 Определитель n-го порядка
- •§ 1.7 Свойства определителей
- •§ 1.8 Взаимная и обратная матрица
Глава 1 Матрицы и определители
§ 1.1. Матрицы и их основные виды
Определение 1. Вещественной матрицей (прямоугольной) размерности m x n называется совокупность mn вещественных чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов.
Если m=n, то матрица называется квадратной, а число n называется ее порядком.
Для обозначения матриц приняты прописные латинские буквы, а для обозначения элементов матриц - строчные:
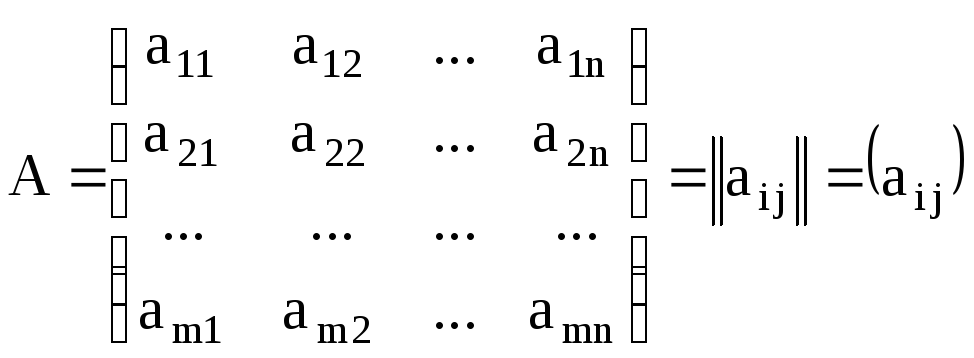 .
.
Здесь
![]() - элемент матрицы
- элемент матрицы
![]() ,стоящий
в строке с номером
,стоящий
в строке с номером
![]() и в столбце с номером
и в столбце с номером
![]() .
.
Определение
2.
Две матрицы А и В одинаковой размерности
m
x
n
называются равными,
если
![]() при всех
при всех
![]() .
.
Элементы
![]() образуют
главную
диагональ
квадратной
матрицы
порядка n,
а элементы
образуют
главную
диагональ
квадратной
матрицы
порядка n,
а элементы
![]() - побочную
(второстепенную)
диагональ
квадратной матрицы.
- побочную
(второстепенную)
диагональ
квадратной матрицы.
Матрицу,
состоящую из одного столбца, называют
матрицей-столбцом
высоты m
и обозначают![]() .
Матрицу, состоящую из одной строки,
называют
матрицей-строкой
длины n
и обозначать
.
Матрицу, состоящую из одной строки,
называют
матрицей-строкой
длины n
и обозначать
![]() .
.
Матрица, все элементы которой равны нулю, называется нулевой и обозначается .
Отметим специальные виды квадратных матриц:
-
Квадратная матрица называется верхней треугольной матрицей, если
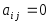 при
при
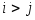 ,
т.е. все элементы, расположенные ниже
главной диагонали равны нулю.
,
т.е. все элементы, расположенные ниже
главной диагонали равны нулю. -
Квадратная матрица называется нижней треугольной матрицей, если
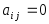 при
при
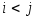 ,
т.е. все элементы, расположенные выше
главной диагонали равны нулю.
,
т.е. все элементы, расположенные выше
главной диагонали равны нулю.
-
Квадратная матрица, у которой
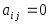 при
при
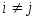 ,
называется диагональной.
Если
у диагональной матрицы
,
называется диагональной.
Если
у диагональной матрицы
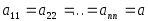 ,
то она называется скалярной.
И, наконец, если в скалярной матрицы
,
то она называется скалярной.
И, наконец, если в скалярной матрицы
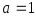 ,
то она называется единичной
матрицей
и обозначается символом I.
,
то она называется единичной
матрицей
и обозначается символом I.
-
Квадратная матрица А называется симметрической, если аij=aji ij
-
Квадратная матрица А называется обратно симметрической, если выполнены условия: элементы аii = 1 i и аij = 1/aji ij.
-
Квадратная матрица А называется кососимметрической, если выполнены условия: элементы аii = 0 I и аij = -aji ij.
Определение
3.
Матрица
![]() размерности n
x
m
называется транспонированной
по
отношению к матрице
размерности n
x
m
называется транспонированной
по
отношению к матрице
![]() размерности m
x
n,
если
размерности m
x
n,
если
![]() .
.
Это
определение означает, что столбцы
матрицы
![]() становятся строками транспонированной
матрицы
становятся строками транспонированной
матрицы
![]() и обратно. Заметим, что для симметрических
А квадратных матриц выполнено: А = АТ
и обратно. Заметим, что для симметрических
А квадратных матриц выполнено: А = АТ
Определение
4.
Прямоугольная матрица А вида
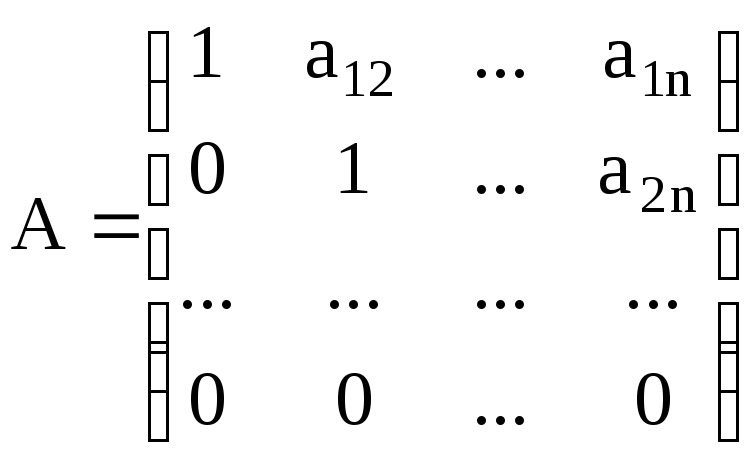 называется верхней трапециевидной.
По аналогии определяется нижняя
трапециевидная
называется верхней трапециевидной.
По аналогии определяется нижняя
трапециевидная
Матрицу
![]() можно разбить системой вертикальных и
горизонтальных прямых на части, которые
при этом рассматриваются как матрицы
низших порядков и называются блоками
или клетками
матрицы
можно разбить системой вертикальных и
горизонтальных прямых на части, которые
при этом рассматриваются как матрицы
низших порядков и называются блоками
или клетками
матрицы
![]() .
Сама матрица, элементами которой служат
блоки, называется блочной
или
клеточной
матрицей.
Общая запись блочной матрицы имеет вид
.
Сама матрица, элементами которой служат
блоки, называется блочной
или
клеточной
матрицей.
Общая запись блочной матрицы имеет вид
 ,
,
где
![]() - клетка-матрица, расположенная в i-ой
клеточной строке и j-ом
клеточном столбце.
- клетка-матрица, расположенная в i-ой
клеточной строке и j-ом
клеточном столбце.
§ 1.2. Линейное пространство
Определение 1. Совокупность объектов, связанных общим свойством , называют множеством и обозначают А = { a ai ak }
Определение 2. Множество чисел К, в котором определены четыре арифметические операции и выполнены все соответствующие свойства этих операций называют полем.
Поля образовывают рациональные, вещественные или комплексные числа. Мы будем рассматривать только поле К вещественных чисел.
Определение 3. Пусть задано множество М, для всех элементов которого определены две операции:
-для любых А, В из М сумма А + В принадлежит М
-для любого А из М и k из К произведение kA принадлежит М
и для этих операций выполняются следующие свойства:
1. Для любых А, В из М выполнено А + В = В + А
2. Для любых А, В, С из М выполнено (А + В) + С = А + (В + С)
3. Для любого А из М найдется «О» из М, что выполнено А + О =А
4. Для любого А из М найдется «-А» из М, что выполнено А+(-А)=0
5. Для любого А из М и , из К выполнено ( + )А = А + В
6. Для любых А, В из М и из К выполнено (А + В) = А + В
7. Для любых А, В из М и , из К выполнено ()А = (А)
8. Для любого А из М найдется 1, что выполнено 1А = А
то множество М называется линейным пространством над полем К.
Замечание.
1).
Множество
![]() всех функций
всех функций
![]() ,
определенных и непрерывных на сегменте
,
определенных и непрерывных на сегменте
![]() ,
образует линейное пространство,
если
,
образует линейное пространство,
если![]() сложение
таких функций и умножение их на
вещественные числа определяются по
обычным правилам математического
анализа.
сложение
таких функций и умножение их на
вещественные числа определяются по
обычным правилам математического
анализа.
2).
Множество
![]() всех алгебраических многочленов степени,
не превышающей фиксированного натурального
числа n,
с операциями, определенными по обычным
правилам операций над многочленами,
образует линейное пространство.
всех алгебраических многочленов степени,
не превышающей фиксированного натурального
числа n,
с операциями, определенными по обычным
правилам операций над многочленами,
образует линейное пространство.
