
- •§ 7. Отображения метрических пространств. Непрерывность отображений
- •Для функционала , заданного формулой , найдите:
- •Функционал задан формулой . Найдите:
- •Дополнительные задания
- •§8. Компактные множества в метрических пространствах
- •Дополнительные задания
- •§ 9. Полные метрические пространства
- •Дополнительные задания
- •§ 10. Принцип сжимающих отображений
- •Дополнительные задания
- •§11. Измеримые множества
- •Дополнительные задания
- •§ 12. Функции, измеримые по Лебегу
- •Дополнительные задания
§ 7. Отображения метрических пространств. Непрерывность отображений
Литература: [1], глава VIII, § 2, глава IX, § 3.
Задачи §7 способствуют более глубокому усвоению таких основных понятий теории функций, как отображение и непрерывность отображения. Студент должен увидеть, что эти понятия являются распространением известных ему понятий числовой функции и ее непрерывности на случай произвольных метрических пространств. Геометрические образы рассматриваемых понятий помогут ему яснее представить структуру определений.
-
Приведите примеры отображений:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
-
Является ли отображением соответствие, заданное уравнением
![]() ,
если:
,
если:
а)
![]() ;
;
б)
![]() ?
?
-
Отображение
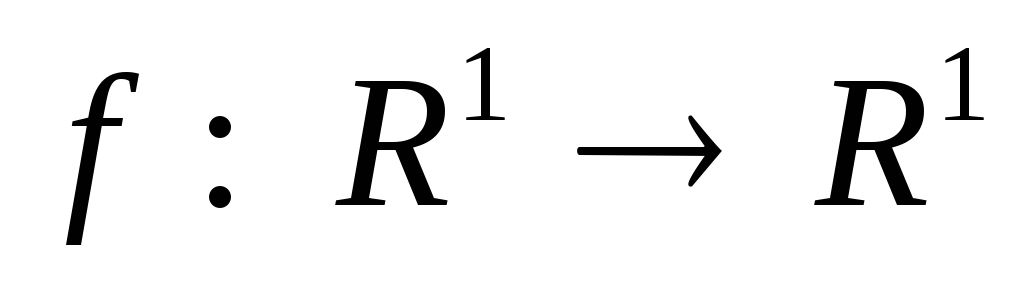 задано формулой
задано формулой
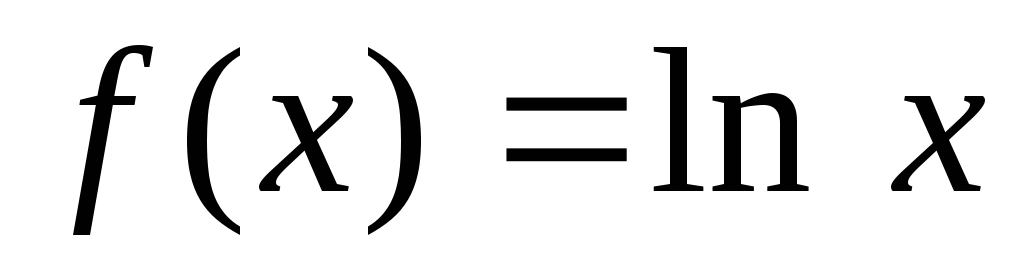 .
Найдите:
.
Найдите:
-
 ;
б)
;
б)
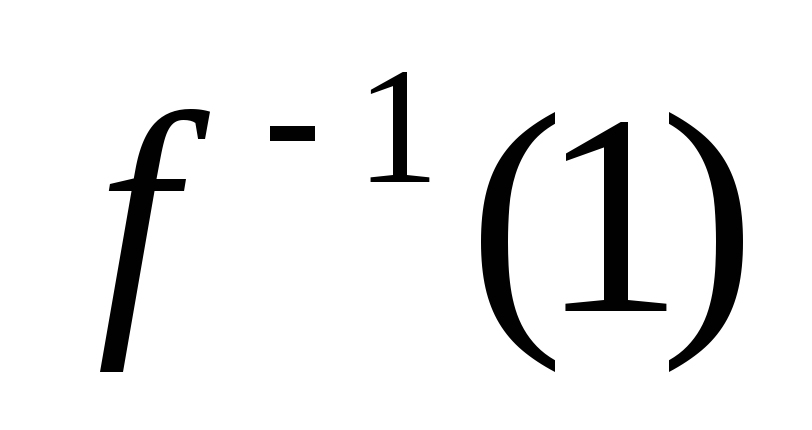 ;
в)
;
в)
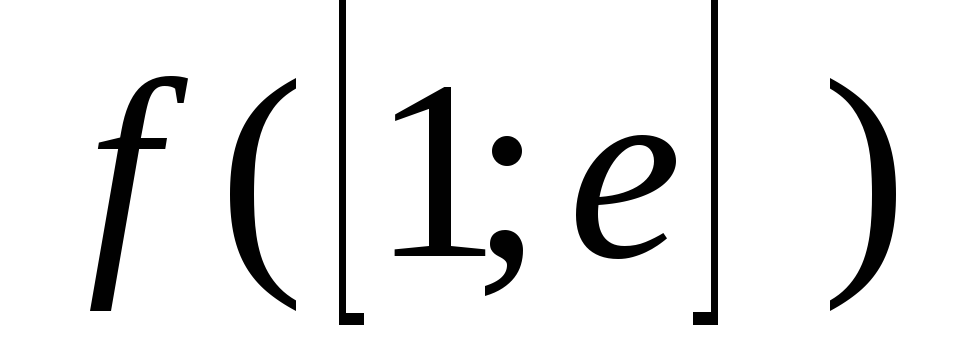 ;
г)
;
г)
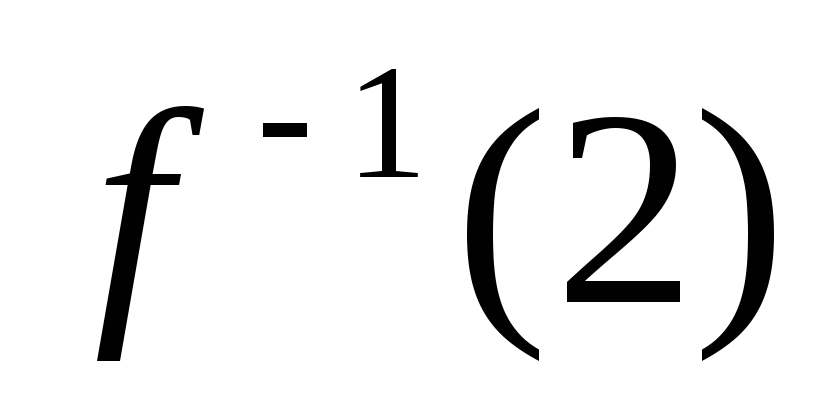 ;
д)
;
д)
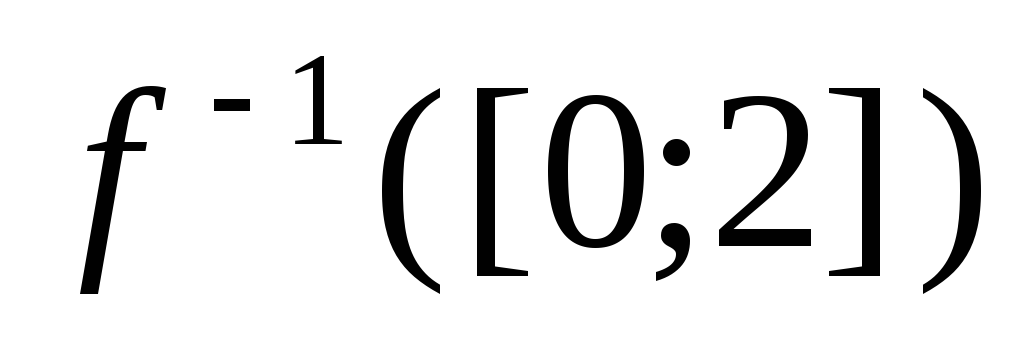 ;
е)
;
е)
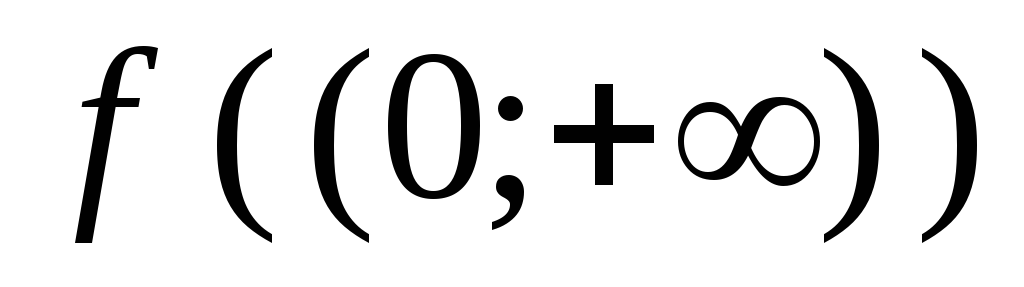 .
.
-
Для отображения
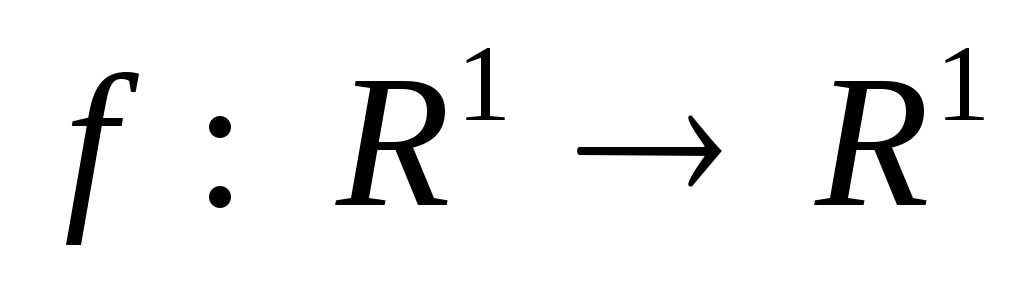 ,
заданного формулой
,
заданного формулой
 ,
найдите: а)
,
найдите: а)
 ;
б)
;
б)
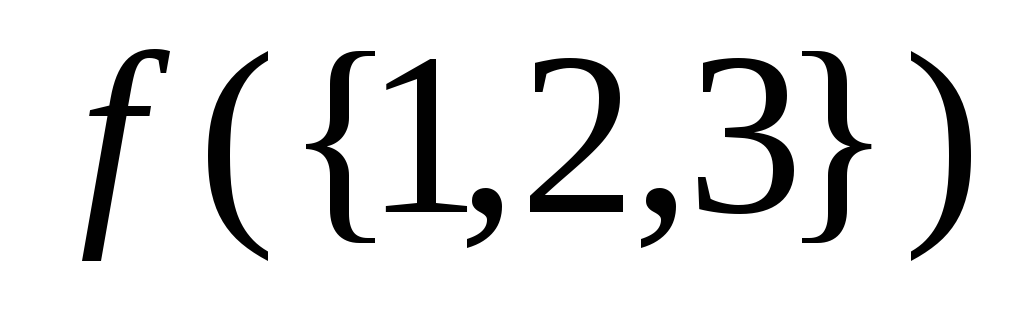 ;
в)
;
в)
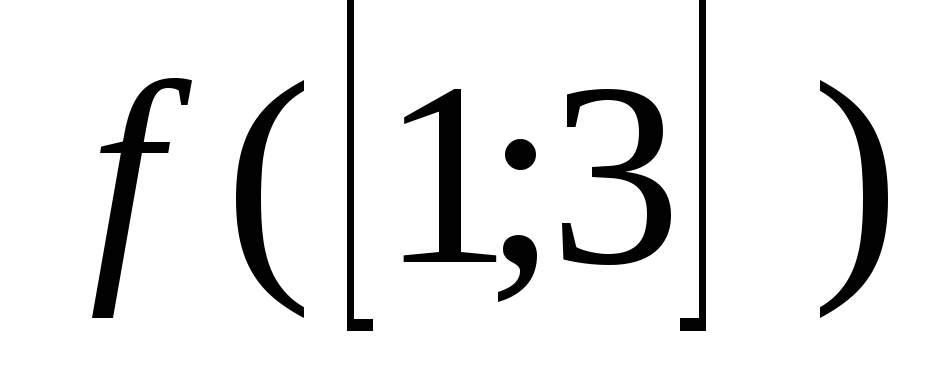 ;
;
г)
![]() ;
д)
;
д)
![]() .
.
-
Для функционала
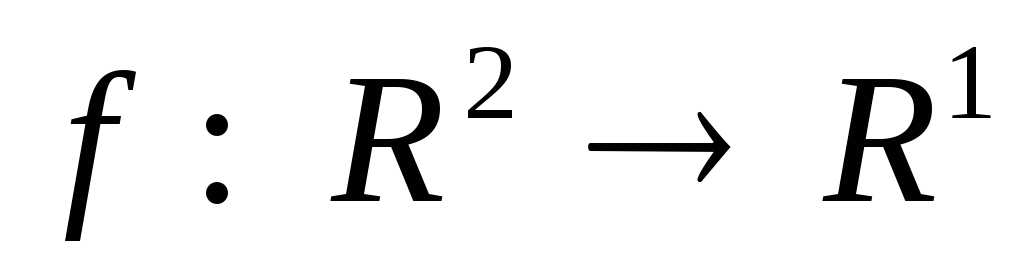 ,
заданного формулой
,
заданного формулой
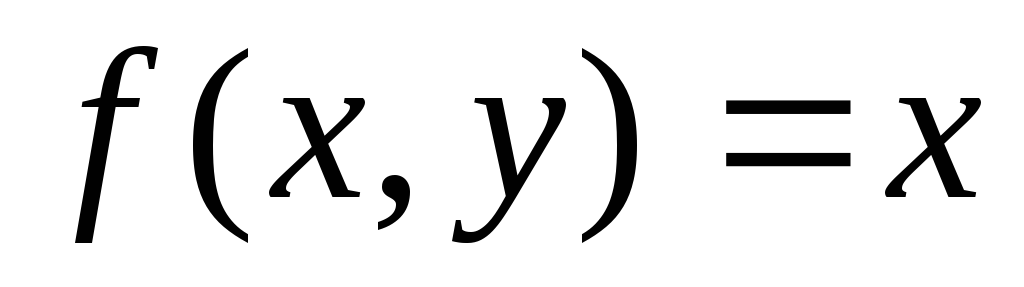 ,
найдите:
,
найдите:
а) образ окружности
![]() ;
б)
;
б)
![]() ;
в) прообраз луча
;
в) прообраз луча
![]() .
.
-
Для функционала , заданного формулой , найдите:
а) образ точки
![]() ;
б) прообраз луча
;
б) прообраз луча
![]() .
.
-
Задано отображение
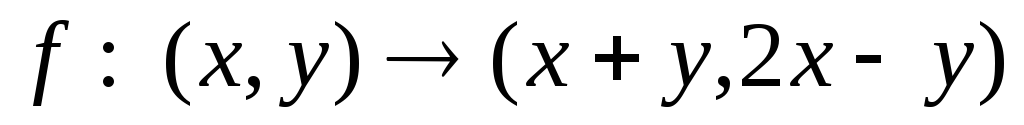 пространства
пространства
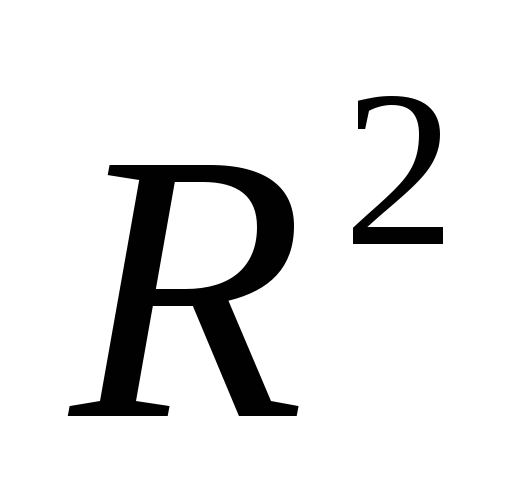 в себя. Найдите: а) образ точки
в себя. Найдите: а) образ точки
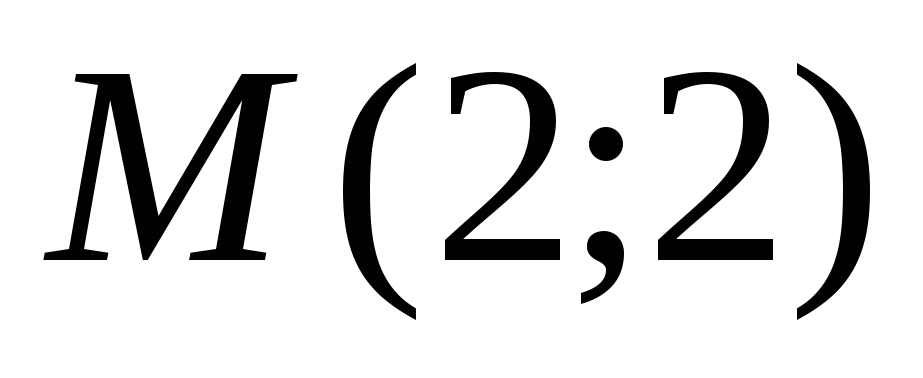 ;
б) прообраз точки
;
б) прообраз точки
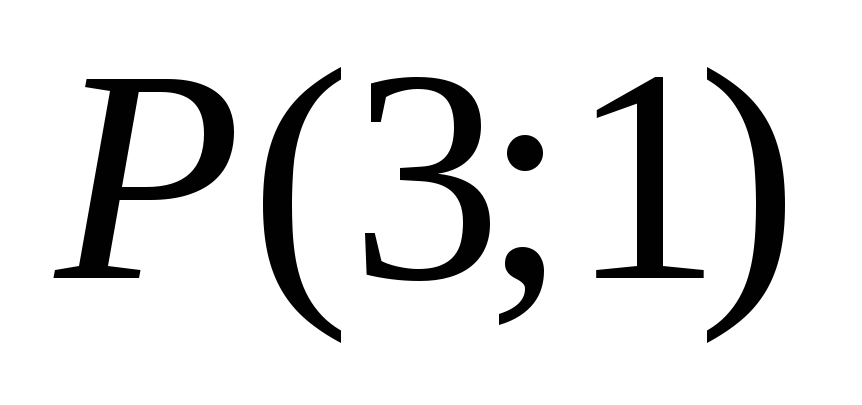 ;
в) образ прямой
;
в) образ прямой
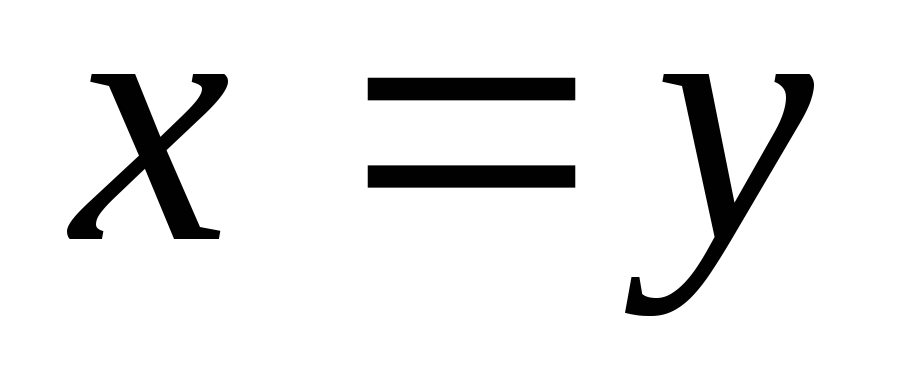 ;
г) прообраз оси абсцисс.
;
г) прообраз оси абсцисс. -
Задайте какое-либо отображение
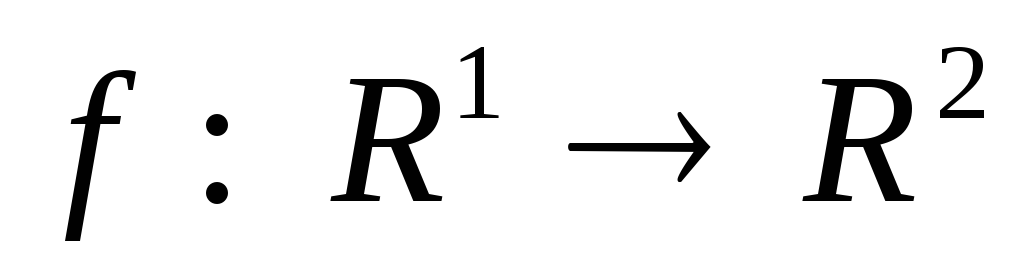 и найдите:
а) образ точки 1; б) прообраз
точки (5;7).
и найдите:
а) образ точки 1; б) прообраз
точки (5;7). -
Функционал
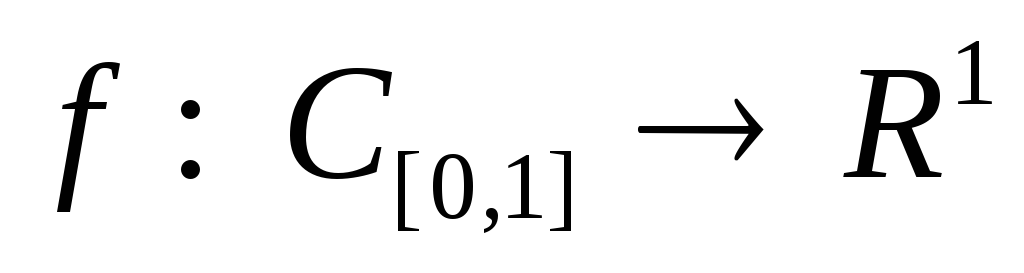 задан формулой
задан формулой
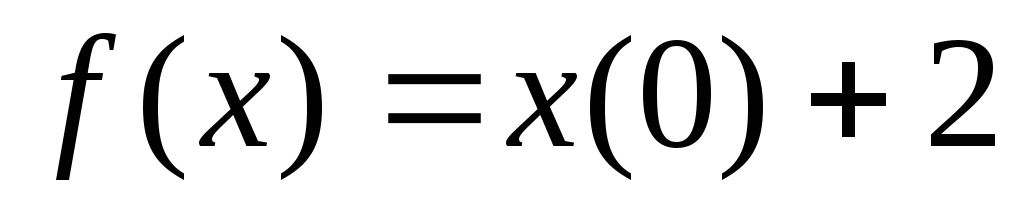 .
Найдите:
.
Найдите:
а) образ точки
![]() ;
;
б) какую-либо точку из прообраза точки 3.
-
Функционал задан формулой . Найдите:
а)
![]() ;
б) какие-либо две точки из прообраза
;
б) какие-либо две точки из прообраза
![]() .
.
-
Установите, существует ли значение
 ,
при котором отображение
,
при котором отображение
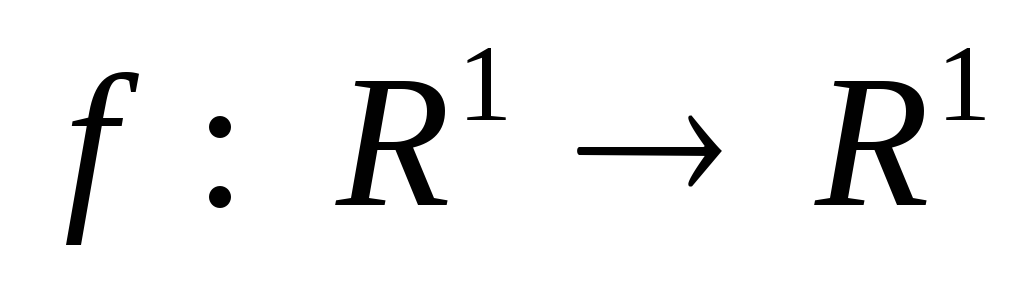 ,
заданное формулами
,
заданное формулами
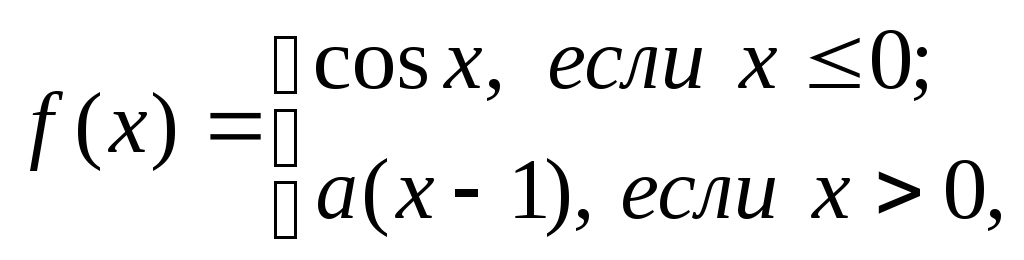 непрерывно.
непрерывно.
Сделайте чертеж.
-
Установите, существуют ли значения
 и
и
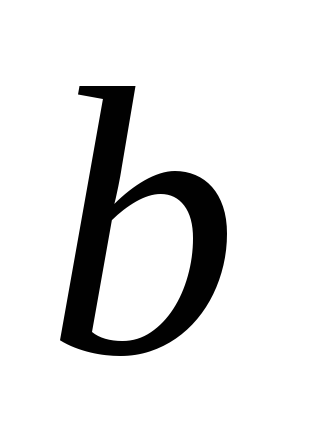 ,
при которых отображение
,
при которых отображение
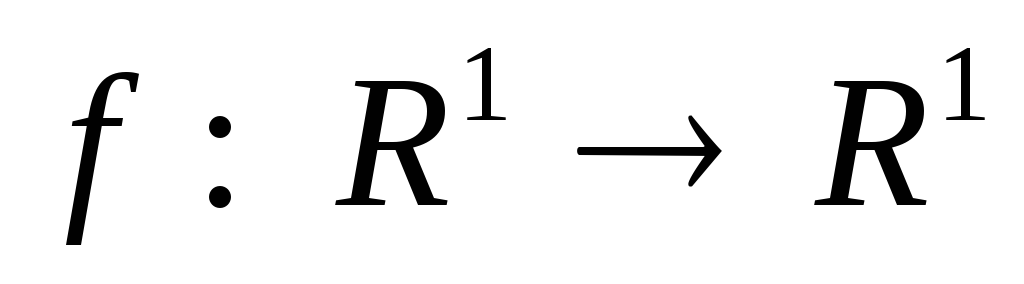 ,
заданное формулами
,
заданное формулами
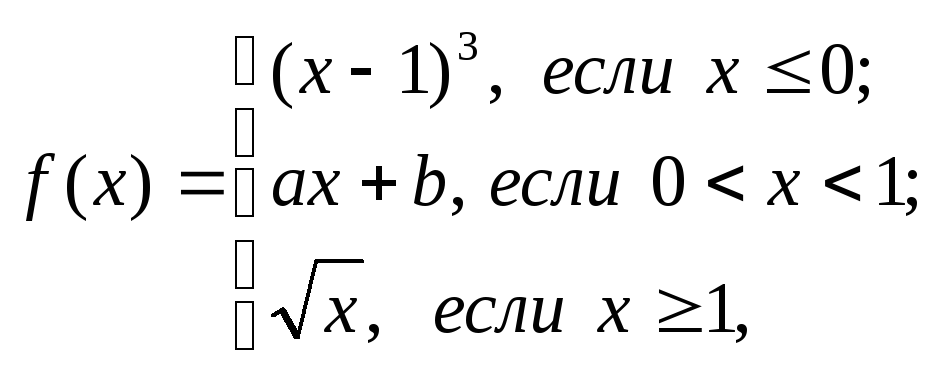 непрерывно.
Сделайте чертеж.
непрерывно.
Сделайте чертеж. -
Функционал
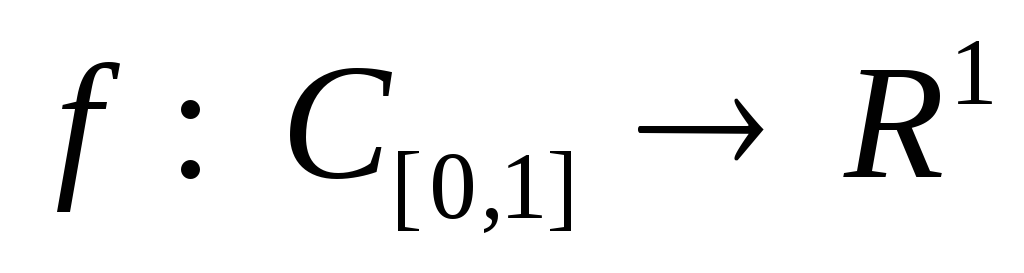 задан формулой
задан формулой
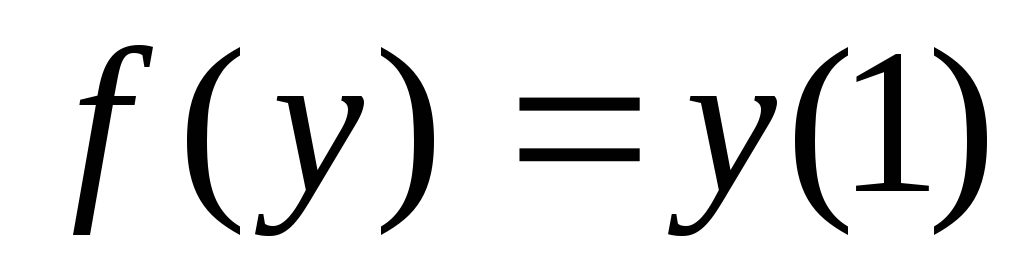 .
Пользуясь определением непрерывности
в точке по Гейне, докажите, что он
непрерывен в пространстве
.
Пользуясь определением непрерывности
в точке по Гейне, докажите, что он
непрерывен в пространстве
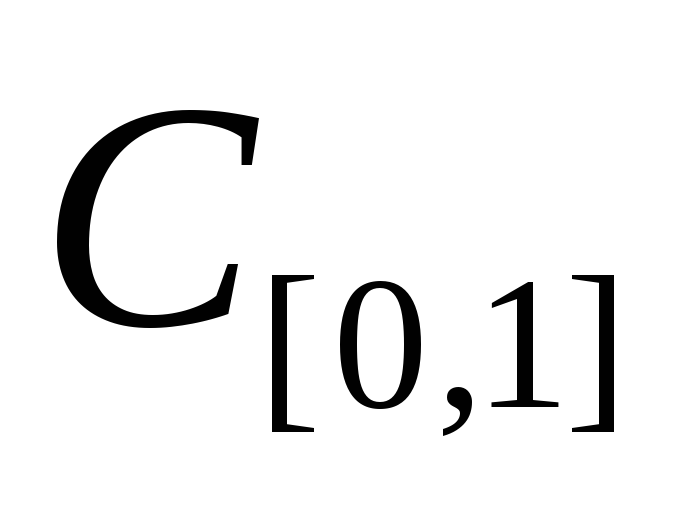 .
. -
Функционал
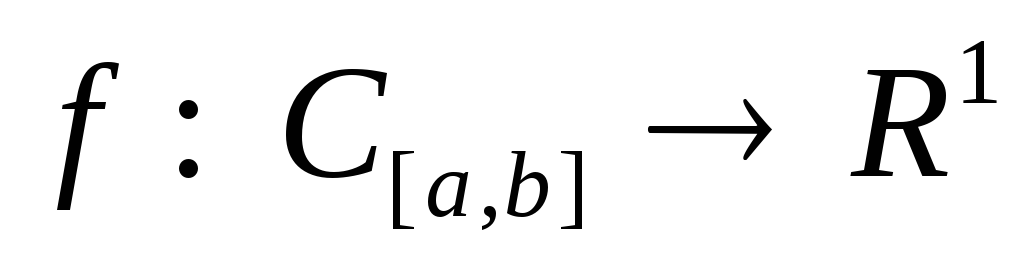 задан формулой
задан формулой
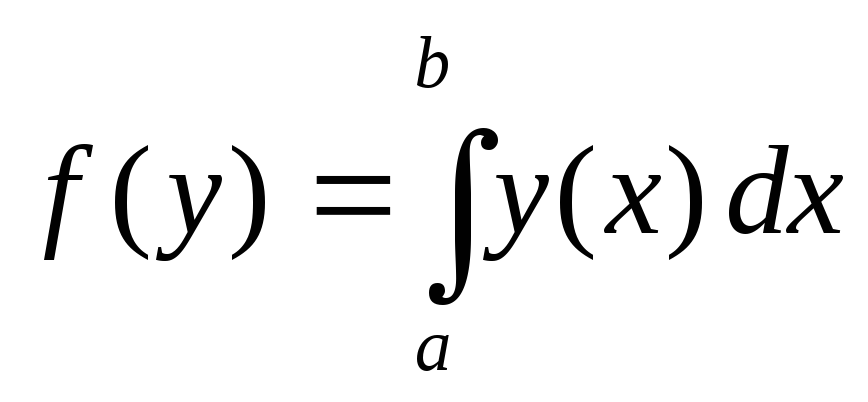 .
Пользуясь определением непрерывности
в точке по Коши, докажите, что он
непрерывен в пространстве
.
Пользуясь определением непрерывности
в точке по Коши, докажите, что он
непрерывен в пространстве
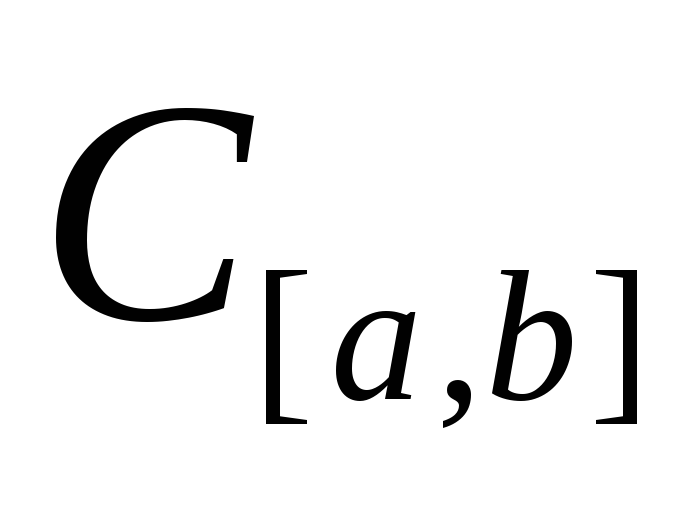 .
. -
Функционал
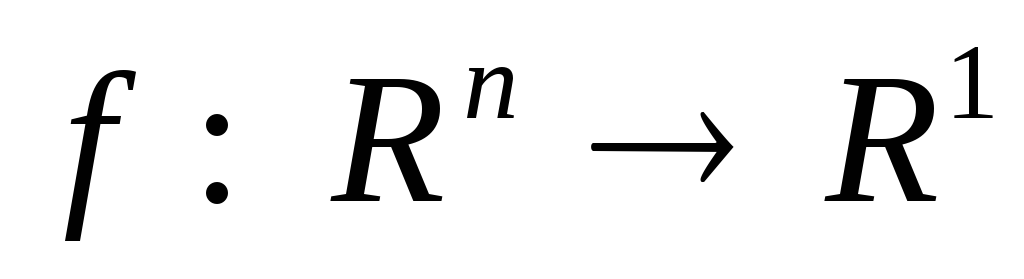 задан формулой
задан формулой
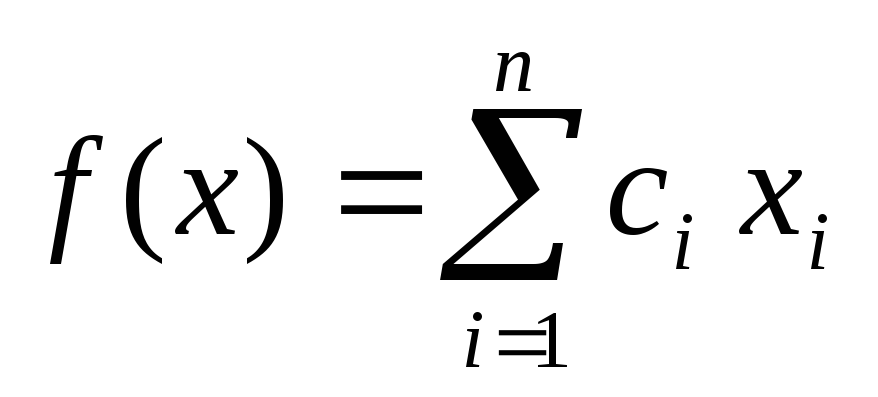 ,
где точка
,
где точка
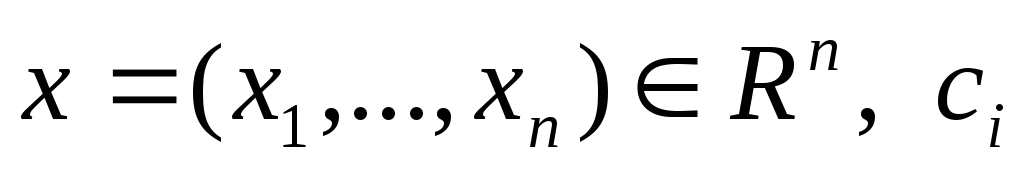 - некоторые заданные числа (
- некоторые заданные числа (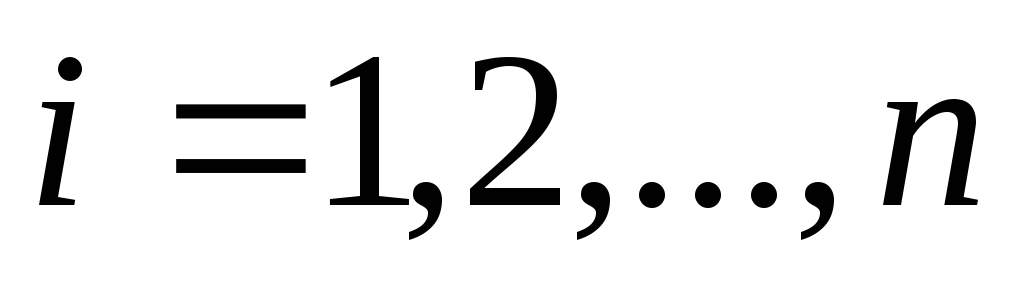 ).
Докажите, что он непрерывен в пространстве
).
Докажите, что он непрерывен в пространстве
 .
. -
Функционал
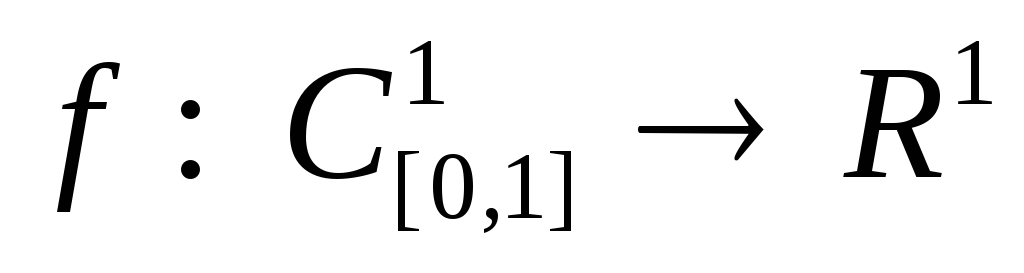 задан формулой
задан формулой
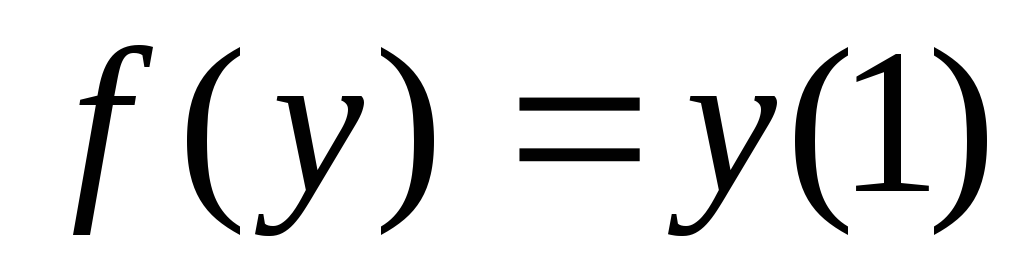 (
(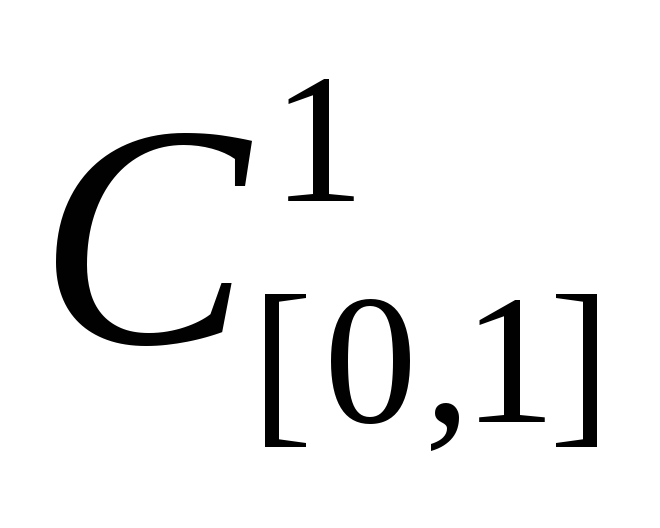 - метрическое пространство всех
непрерывных на отрезке
- метрическое пространство всех
непрерывных на отрезке
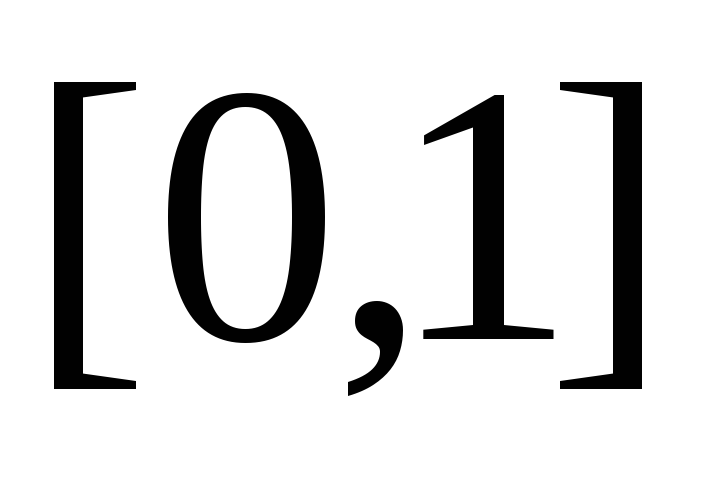 функций, где за расстояние между
функциями
функций, где за расстояние между
функциями
 и
и
 принято число
принято число
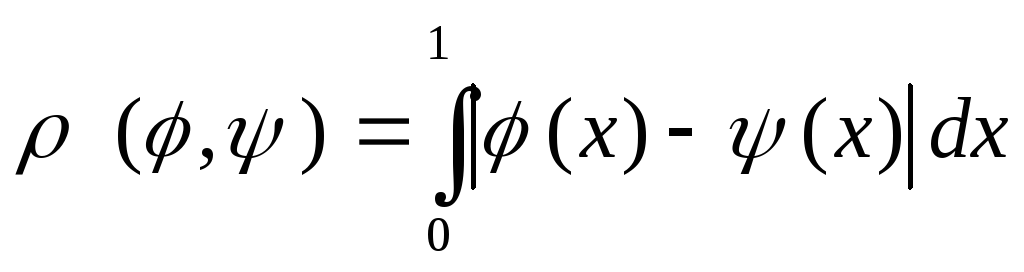 ).
Выясните, является ли данный функционал
непрерывным в точке
).
Выясните, является ли данный функционал
непрерывным в точке
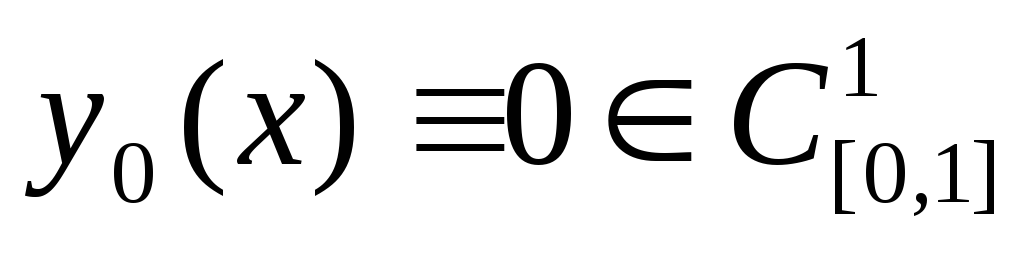 .
. -
Отображение
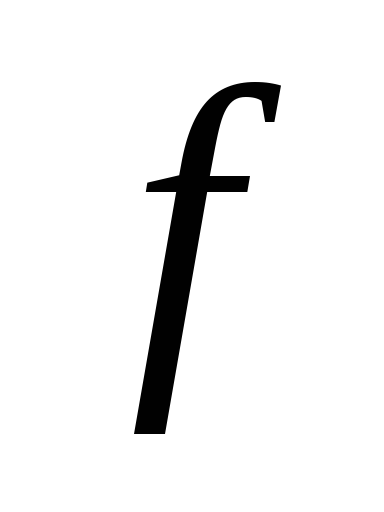 подпространства
подпространства
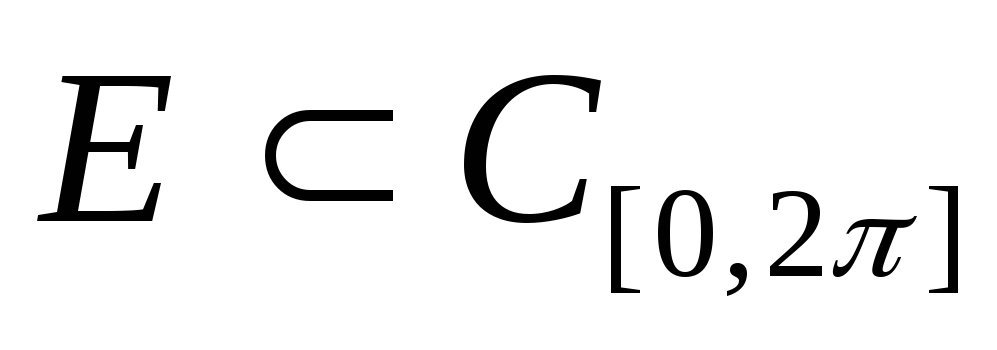 ,
состоящего из непрерывно дифференцируемых
функций, в пространство
,
состоящего из непрерывно дифференцируемых
функций, в пространство
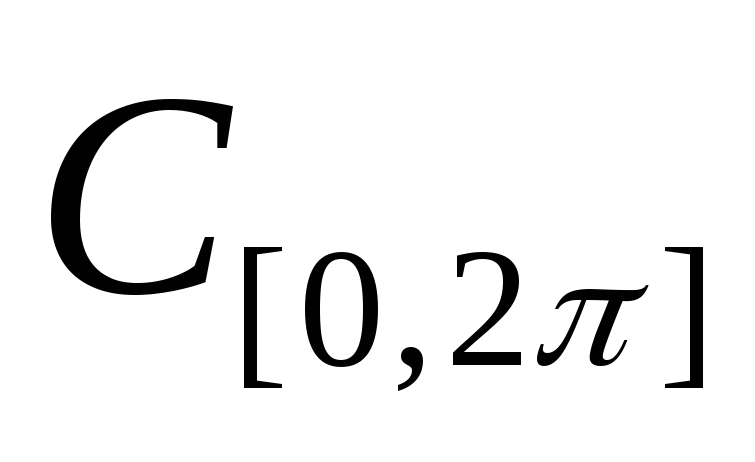 задано формулой
задано формулой
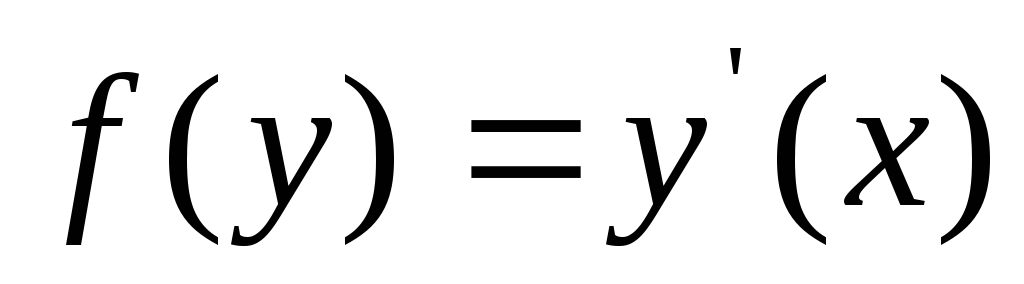 .
Выясните, является ли это отображение
непрерывным в точке
.
Выясните, является ли это отображение
непрерывным в точке
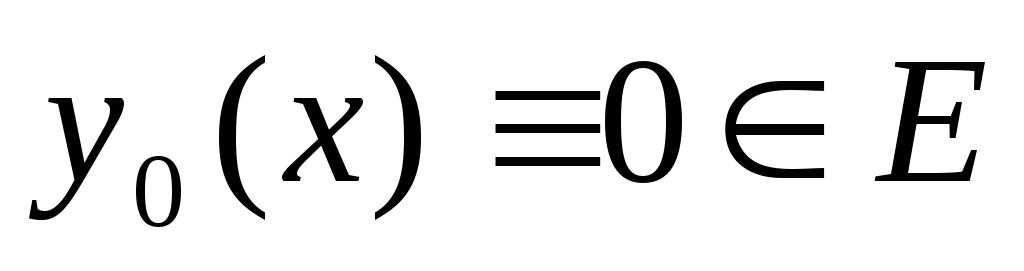 .
. -
Верно ли, что при непрерывном отображении образ открытого множества является открытым множеством?
-
Верно ли, что при непрерывном отображении образ замкнутого множества является замкнутым множеством?
-
С помощью теоремы о необходимом и достаточном условии непрерывности отображения одного метрического пространства в другое, докажите, что множество
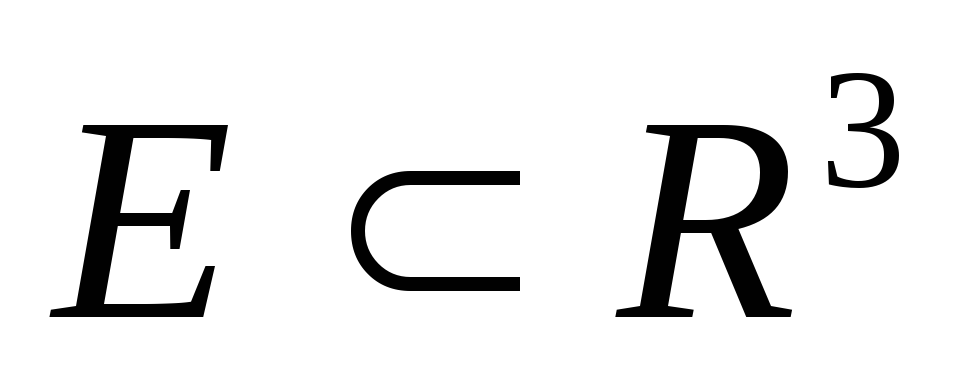 ,
определяемое неравенством
,
определяемое неравенством
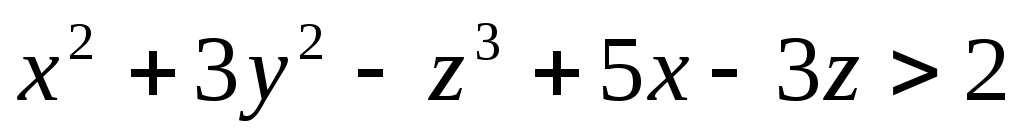 ,
открыто.
,
открыто.
