4. Властивості операцій над множинами

Операції над множинами, як і операції над числами, мають певні властивості. Ці властивості виражаються сукупністю тотожностей незалежно від конкретного змісту множин, що входять у них, і є підмножинами деякого універсуму .

Для будь-яких підмножин деякого універсуму справедливі наступні тотожності:

1. –комутативність	1*. – комутативність
2. – асоціативність	2*. – асоціативність
3. - дистрибутивність відносно	3*. - дистрибутивність відносно
закони де Моргана
4.	4*.
5.
закони ідемпотентності
6.	6*.
властивості і
7.	7*.
8.	8*.
9.
10.
11.

Приклад. Перевірити справедливість співвідношення для множин

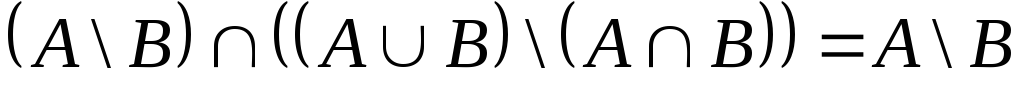
за допомогою властивостей операцій над множинами:

Розв’язання.

Властивість 10;

Властивість 4;

Властивість 2;

Властивість 1;

Властивості 2, 3;

Властивість 8;

Властивості 7^*, 1 ;

Властивість 6;

Властивість 10

.

5. Декартовий добуток множин

Означення. Послідовність з елементів, розташованих в певному порядку називається набором (вектором, кортежем) довжини . Позначається через . Елементи набору називаються його компонентами (координатами).

Набір довжини 2 називається упорядкованою парою, довжини 3 – упорядкованою трійкою,…, довжини – упорядкованою -кою.

Означення. Два набори називаються рівними, якщо рівні їх довжини і відповідні елементи збігаються:

= і , , …,

Означення. Декартовим добутком множин і називається множина , яка складається з усіх пар таких, що :

=;

.

Означення. Декартовим добутком множин множин називається множина , яка складається з усіх наборів таких, що :

У випадку застосування операції декартового добутку до однакових множин зручно записувати . Такий декартовий добуток називають -м степенем множини .

= – декартовий квадрат множини .

Приклад . Знайти і зобразити в ПДСК множину , якщо

, ;

Розв’язання.

;

6. – арні відношення на множинах (множині).

Бінарні відношення. Властивості бінарних відношень.

Означення. Довільна підмножина називається n-арним відношенням на множинах . Кажуть, що знаходяться у відношенні (або зв’язані відношенням ), якщо набір .

При маємо бінарне відношення на множинах і :.

Якщо два елементи знаходяться у відношенні , то записуємо . Якщо ж два елементи не зв’язані відношенням , то записуємо , або .

Приклад 1. Нехай . Визначимо на цій множині відношення : . Явний запис відношення має вигляд:

.

Відношення можна подати графічно. Графічні представлення відношень мають властивість наочності (при невеликих ) і можливі в наступних формах:

1. Графіки. В декартовій системі координат на осях (ось абсцис відповідає області визначення , ось ординат - області значень ) відмічаються точки, які являють собою елементи множин і , на яких визначено відношення . Потім відмічаються точки з координатами , в яких , .

Наприклад, графік відношення з прикладу 1 має такий вигляд:

2. Стрілкова схема. Будується графічна діаграма у вигляді множин точок (вузлів), які являють собою елементи множин і . Потім з’єднуються стрілками пари точок, які входять у відношення .

Стрілкова схема для приклада 1 має вигляд: