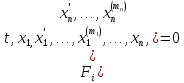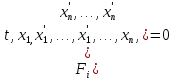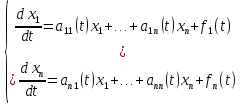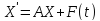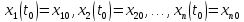-
Система дифференциальных уравнений
Системой дифференциальных уравнений называется система уравнений, связывающих независимую переменную t, неизвестные функции x1(t), …,xn(t) этой
|
|
(6) |
где Fi – функции указанных аргументов, заданные в некоторой области их определения.
Наибольшее из чисел m1,…,mn, называется порядком системы (6). При m1=…=mn= 1 система (6) называется системой первого порядка
|
|
(7) |
Если l = n и уравнения можно разрешить относительно производных, то (7) можно переписать в виде
|
|
(8) |
где
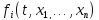 ,
i
= 1,…, n,
- известные
функции.
,
i
= 1,…, n,
- известные
функции.
Система (8) называется нормальной системой или системой, записанной в нормальной форме Коши.
Порядком нормальной системы (8) называется число входящих в нее уравнений.
Система
называется линейной , если функция
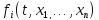 i
= 1,…, n
линейно зависят от неизвестной функции
i
= 1,…, n
линейно зависят от неизвестной функции
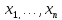 :
:
|
|
(9) |
где aij(t), fi(t), i,j = 1,…, n –заданные функции переменной t.
Если все функции aij(t), i,j = 1,…, n не зависят от е, то есть aij(t) = aij = const, то система
|
|
(10) |
называется линейной системой с постоянными коэффициентами.
Система (10) называется однородной системой.
Решение
системы представляет собой совокупность
n
функций
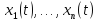 ,
непрерывных
на некотором интервале
(a,
b),
такая, что подстановка этих функций в
(8) обращает каждое уравнение в тождество.
,
непрерывных
на некотором интервале
(a,
b),
такая, что подстановка этих функций в
(8) обращает каждое уравнение в тождество.
Задача Коши для системы (8) состоит в нахождении решения системы (8), удовлетворяющего начальным условиям:
|
|
(11) |
Геометрический смысл данной задачи состоит в том, что ищется та интегральная кривая, которая проходит через точку (t0, x10, x20, …, xn0) пространства Rn+1.
-
Обзор численных методов численного решения обыкновенных дифференциальных уравнений и систем
Численные методы решения обыкновенных дифференциальных уравнений и систем являются самым важным приложением теории дифференциальных уравнений. Большинство практических моделей динамических систем исследуются именно с помощью численных методов, поскольку модели реальных явлений, как правило, описываются достаточно сложными для аналитического исследования выражениями.
Процесс получения приближенного решения в огромной степени ориентирован на квалифицированное использование современной вычислительной техники. Совокупность численных методов представляет мощный и эффективный аппарат решения многих инженерных задач.
Существующие
численные методы можно представить в
виде следующей схемы:
Явные методы
Явный метод Эйлера
Метод Эйлера-Коши
Модифицированный метод Эйлера
Метод предсказания и коррекции
Явные методы
Рунге-Кутты
Метод Рунге-Кутты-Мерсона
Метод Адамса-Башфорта
Методы Фельберга
Методы Ингленда
Явные методы Мильна
Методы Нюстрема
Явные методы Хемминга
Экстраполяционные методы