|
Билет
9. Канонический
вид уравнений Эйлера.
Канонич
вид ур-ния Эйлера можно получить,
перейдя к канонич переменным.
Рассм
случай трёхмерного пространства,
когда основной интеграл имеет вид:
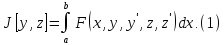
Ур-ния
Эйлера для этого интеграла:
 представляют
собой сист двух ур второго порядка.
Введём вместо представляют
собой сист двух ур второго порядка.
Введём вместо
 и
и
 новые переменные
новые переменные
 и
и
 по формулам:
по формулам:
 причём
написанные ур-ния разрешимы относительно причём
написанные ур-ния разрешимы относительно
 и
и
 ,
т.е. что соответствующ функциональный
определитель отличен от нуля: ,
т.е. что соответствующ функциональный
определитель отличен от нуля:
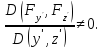 Введём
ещё вместо Введём
ещё вместо
 новую функцию
новую функцию
 : :
 и
будем считать H
выраженной через новые переменные и
будем считать H
выраженной через новые переменные
 и
и
 .
Определим частн производн от функц .
Определим частн производн от функц
 по последним четырём переменным:
по последним четырём переменным:
 или,
в силу (3): или,
в силу (3):
 Точно
так же при помощи простого дифференцирования
получим: Точно
так же при помощи простого дифференцирования
получим:
 Т
.о., вместо двух ур-ний второго порядка
(2) мы можем в новых переменных написать
сист четырёх уравн первого порядка
для функц Т
.о., вместо двух ур-ний второго порядка
(2) мы можем в новых переменных написать
сист четырёх уравн первого порядка
для функц
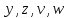 независимой переменной
независимой переменной
 : :
 Система
(6) называется канонической
системой Эйлера.
Из формул (4) и (5) непосредственно
получается выражение подинтегральной
функции Система
(6) называется канонической
системой Эйлера.
Из формул (4) и (5) непосредственно
получается выражение подинтегральной
функции
 функционала через функцию
функционала через функцию
 : :
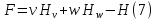
|
Билет
10. Вариационные
задачи с подвижными концами.
Положим, что мы
ищем экстремум интеграла
 причём
левый конец искомой кривой закреплён,
т.е. на левом конце имеется предельное
условие причём
левый конец искомой кривой закреплён,
т.е. на левом конце имеется предельное
условие
 ,
а на правый конец никакого условия не
наложено, кроме того этот конец должен
находиться на прямой ,
а на правый конец никакого условия не
наложено, кроме того этот конец должен
находиться на прямой
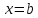 ,
параллельн оси ,
параллельн оси
 .
Покажем, что на таком свободн конце
должно быть также выполнено некотор
предельн услов, котор непосредственно
получится из услов экстремума интеграла
(1). Действит, если некотор кривая даёт
экстремум интегралу (1) по сравнению
со всеми близкими кривыми со свободн
прав концом, то тем более она даёт
экстремум интегралу (1) при услов
закрепления правого конца. Но тогда
она должна удовлетворять ур-нию Эйлера,
т.е. быть экстремалью интеграла
(1).
общее выражение первой вариации
интеграла (1): .
Покажем, что на таком свободн конце
должно быть также выполнено некотор
предельн услов, котор непосредственно
получится из услов экстремума интеграла
(1). Действит, если некотор кривая даёт
экстремум интегралу (1) по сравнению
со всеми близкими кривыми со свободн
прав концом, то тем более она даёт
экстремум интегралу (1) при услов
закрепления правого конца. Но тогда
она должна удовлетворять ур-нию Эйлера,
т.е. быть экстремалью интеграла
(1).
общее выражение первой вариации
интеграла (1):
 Эта
первая вариация должна обращаться в
нуль. Член, содержащ интеграл, равен
нулю, поскольку функц Эта
первая вариация должна обращаться в
нуль. Член, содержащ интеграл, равен
нулю, поскольку функц
 ,
должна и в этом случае удовлетворять
ур-нию Эйлера. Внеинтегральный член
должен обращаться в нуль при ,
должна и в этом случае удовлетворять
ур-нию Эйлера. Внеинтегральный член
должен обращаться в нуль при
 ,
так как этот конец является закреплённым.
Т. о., равенство нулю первой вариации
приводит нас к равенству ,
так как этот конец является закреплённым.
Т. о., равенство нулю первой вариации
приводит нас к равенству
 при
при
 .
На свободном конце .
На свободном конце
 может быть произвольным, и окончательно
мы получаем на свободном конце след
предельн услов:
может быть произвольным, и окончательно
мы получаем на свободном конце след
предельн услов:
 Оно
даёт нам некоторую связь между Оно
даёт нам некоторую связь между
 и
и
 на свободн конце. Нетрудно проверить,
что для интеграла (1) условие (2) будет
иметь вид
на свободн конце. Нетрудно проверить,
что для интеграла (1) условие (2) будет
иметь вид
 ,
т.е. в случае интеграла (1) оно сводится
к требованию, чтобы на конце ,
т.е. в случае интеграла (1) оно сводится
к требованию, чтобы на конце
 экстремаль была перпендикулярна к
прямой
экстремаль была перпендикулярна к
прямой
 .
Предельное условие (2) называется
обычно естественным
предельным
или граничным
условием. .
Предельное условие (2) называется
обычно естественным
предельным
или граничным
условием.
|
Билет
11. Вариационные
задачи с подвижными границами. Условия
трансверсальности.
При
рассмотрении естественных предельн
услов мы считали, что конец экстремали
может перемещаться по прямой
 или
или
 ,
параллельн оси ,
параллельн оси
 .
Положим теперь, что он может перемещаться
по любой заданной линии .
Положим теперь, что он может перемещаться
по любой заданной линии
 на плоск
на плоск
 .
Для определённости будем считать, что
лев конец .
Для определённости будем считать, что
лев конец
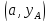 закреплён, а правый может перемещаться
по
закреплён, а правый может перемещаться
по
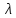 .
Рассуждая, как в Билете 5, докажем, что
если некотор кривая .
Рассуждая, как в Билете 5, докажем, что
если некотор кривая
 даёт экстремум интегралу, то она должна
удовлетвор ур-нию Эйлера, т.е. быть
экстремалью. Первая вариац должна
обращаться в нуль: слагаемое, содержащ
знак интеграла, будет равно нулю в
силу ур-ния Эйлера, а внеинтегральный
член при
даёт экстремум интегралу, то она должна
удовлетвор ур-нию Эйлера, т.е. быть
экстремалью. Первая вариац должна
обращаться в нуль: слагаемое, содержащ
знак интеграла, будет равно нулю в
силу ур-ния Эйлера, а внеинтегральный
член при
 будет равен нулю в силу условия
закрепления конца. Т. о., равенство
нулю первой вариации приводит нас к
следующ услов на подвижном конце:
будет равен нулю в силу условия
закрепления конца. Т. о., равенство
нулю первой вариации приводит нас к
следующ услов на подвижном конце:
 где где
 и
и
 – проекции на коорд оси бесконечно
малого перемещен вдоль кривой
– проекции на коорд оси бесконечно
малого перемещен вдоль кривой
 .
Если бы мы считали оба конца подвижными,
то получили бы на обоих концах предельн
условие (1). Достаточно повторить
предыдущ рассужден, помня, что если
кривая даёт экстремум интегралу при
подвижн концах, то тем более она даёт
экстремум при неподвижн концах или
при неподвижн одном конце. .
Если бы мы считали оба конца подвижными,
то получили бы на обоих концах предельн
условие (1). Достаточно повторить
предыдущ рассужден, помня, что если
кривая даёт экстремум интегралу при
подвижн концах, то тем более она даёт
экстремум при неподвижн концах или
при неподвижн одном конце.
Обозначая через
 угловой коэфт касательной к кривой
угловой коэфт касательной к кривой
 ,
можем переписать услов (1) в виде: ,
можем переписать услов (1) в виде:
 т.
о. это условие, называемое обычно
условием
трансверсальности,
устанавливает связь между угловым
коэф т.
о. это условие, называемое обычно
условием
трансверсальности,
устанавливает связь между угловым
коэф
 касательной к экстремали и угловым
коэф
касательной к экстремали и угловым
коэф
 касательной к кривой
касательной к кривой
 в каждой точке этой кривой. Если ур-ние
в каждой точке этой кривой. Если ур-ние
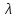 задано в неявной форме
задано в неявной форме
 ,
то условие трансверсальности может
быть переписано в виде: ,
то условие трансверсальности может
быть переписано в виде:
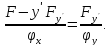
|



 ,
подставим в интеграл (1), продифференц
по
,
подставим в интеграл (1), продифференц
по
 и положим
и положим
 .:
.:



 и её производн до порядка
и её производн до порядка
 обращаются в нуль на концах
обращаются в нуль на концах
 ю
Вследствие этого внеинтегральные
члены пропадут; приравнивая к нулю
ю
Вследствие этого внеинтегральные
члены пропадут; приравнивая к нулю
 ,
получим условие:
,
получим условие: которое,
в силу основной леммы Дюбуа-Реймона,
приводит нас к следующему уравнению
Эйлера:
которое,
в силу основной леммы Дюбуа-Реймона,
приводит нас к следующему уравнению
Эйлера:

 .
Его общий интеграл содержит
.
Его общий интеграл содержит
 произвольн пост, и мы должны иметь ещё
произвольн пост, и мы должны иметь ещё
 предельн услов. В простейшем случ эти
услов сводятся к заданию функц и её
производных до порядка
предельн услов. В простейшем случ эти
услов сводятся к заданию функц и её
производных до порядка
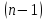 на концах промежутка
на концах промежутка
 .
Из этих предельн услов и вытекает, что
аналогичн величины для
.
Из этих предельн услов и вытекает, что
аналогичн величины для
 должны обращаться в нуль. Отметим ещё,
что мы считаем непрерывн все те функц,
котор входят в предыдущ формулы, так
что, например, искомую функц
должны обращаться в нуль. Отметим ещё,
что мы считаем непрерывн все те функц,
котор входят в предыдущ формулы, так
что, например, искомую функц
 мы считаем принадлежащей классу
мы считаем принадлежащей классу
 функц, непрерывных со своими производными
до порядка
функц, непрерывных со своими производными
до порядка
 .
. где
где
 и
и
 частные производн функц
частные производн функц
 .
Ищется функц
.
Ищется функц
 ,
непрерывн со своими производн до
второго порядка в области
,
непрерывн со своими производн до
второго порядка в области
 ,
имеющая заданные знач на контуре
,
имеющая заданные знач на контуре
 этой области и дающая экстремум
функционалу (1). Составляем близкие
функц
этой области и дающая экстремум
функционалу (1). Составляем близкие
функц
 где
где
 – произвольн функц, обращающаяся в
нуль на
– произвольн функц, обращающаяся в
нуль на
 .
Подставляя эту функц в интеграл (1),
диф-руя по
.
Подставляя эту функц в интеграл (1),
диф-руя по
 и полагая
и полагая
 ,
получ выраж первой вариации
функционала:
,
получ выраж первой вариации
функционала:
 Преобразуем
последние два слагаем, пользуясь
известной ф-лой Римана:
Преобразуем
последние два слагаем, пользуясь
известной ф-лой Римана:
 следующим
образом:
следующим
образом:


 Т.о.
выражение первой вариации:
Т.о.
выражение первой вариации:
 Для
экстремума необх, чтобы эта первая
вариация обращалась в нуль, или,
принимая во внимание, что
Для
экстремума необх, чтобы эта первая
вариация обращалась в нуль, или,
принимая во внимание, что
 на
на
 равно нулю, мы можем утверждать, что
двойной интеграл, стоящий в правой
части (2), должен равняться нулю, а
отсюда, в силу основной леммы
Дюбуа-Реймона, мы получаем для искомой
функции
равно нулю, мы можем утверждать, что
двойной интеграл, стоящий в правой
части (2), должен равняться нулю, а
отсюда, в силу основной леммы
Дюбуа-Реймона, мы получаем для искомой
функции
 ,
дающей экстремум функционалу (1),
следующее ур-ние Остроградского-Гаусса:
,
дающей экстремум функционалу (1),
следующее ур-ние Остроградского-Гаусса:
 или
в раскрытом виде:
или
в раскрытом виде:
 получили
ур-ние с частн производн второго
порядка, котор должно быть удовлетворено
внутри области
получили
ур-ние с частн производн второго
порядка, котор должно быть удовлетворено
внутри области
 .
Предельн услов явл задание
.
Предельн услов явл задание
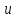 на контуре
на контуре
 .
.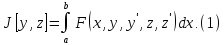
 представляют
собой сист двух ур второго порядка.
Введём вместо
представляют
собой сист двух ур второго порядка.
Введём вместо
 и
и
 новые переменные
новые переменные
 и
и
 по формулам:
по формулам:
 причём
написанные ур-ния разрешимы относительно
причём
написанные ур-ния разрешимы относительно
 и
и
 ,
т.е. что соответствующ функциональный
определитель отличен от нуля:
,
т.е. что соответствующ функциональный
определитель отличен от нуля:
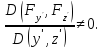 Введём
ещё вместо
Введём
ещё вместо
 новую функцию
новую функцию
 :
:
 и
будем считать H
выраженной через новые переменные
и
будем считать H
выраженной через новые переменные
 и
и
 .
Определим частн производн от функц
.
Определим частн производн от функц
 по последним четырём переменным:
по последним четырём переменным:
 или,
в силу (3):
или,
в силу (3):
 Точно
так же при помощи простого дифференцирования
получим:
Точно
так же при помощи простого дифференцирования
получим:
 Т
.о., вместо двух ур-ний второго порядка
(2) мы можем в новых переменных написать
сист четырёх уравн первого порядка
для функц
Т
.о., вместо двух ур-ний второго порядка
(2) мы можем в новых переменных написать
сист четырёх уравн первого порядка
для функц
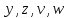 независимой переменной
независимой переменной
 :
:
 Система
(6) называется канонической
системой Эйлера.
Из формул (4) и (5) непосредственно
получается выражение подинтегральной
функции
Система
(6) называется канонической
системой Эйлера.
Из формул (4) и (5) непосредственно
получается выражение подинтегральной
функции
 функционала через функцию
функционала через функцию
 :
:
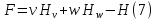
 причём
левый конец искомой кривой закреплён,
т.е. на левом конце имеется предельное
условие
причём
левый конец искомой кривой закреплён,
т.е. на левом конце имеется предельное
условие
 ,
а на правый конец никакого условия не
наложено, кроме того этот конец должен
находиться на прямой
,
а на правый конец никакого условия не
наложено, кроме того этот конец должен
находиться на прямой
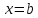 ,
параллельн оси
,
параллельн оси
 .
Покажем, что на таком свободн конце
должно быть также выполнено некотор
предельн услов, котор непосредственно
получится из услов экстремума интеграла
(1). Действит, если некотор кривая даёт
экстремум интегралу (1) по сравнению
со всеми близкими кривыми со свободн
прав концом, то тем более она даёт
экстремум интегралу (1) при услов
закрепления правого конца. Но тогда
она должна удовлетворять ур-нию Эйлера,
т.е. быть экстремалью интеграла
(1).
общее выражение первой вариации
интеграла (1):
.
Покажем, что на таком свободн конце
должно быть также выполнено некотор
предельн услов, котор непосредственно
получится из услов экстремума интеграла
(1). Действит, если некотор кривая даёт
экстремум интегралу (1) по сравнению
со всеми близкими кривыми со свободн
прав концом, то тем более она даёт
экстремум интегралу (1) при услов
закрепления правого конца. Но тогда
она должна удовлетворять ур-нию Эйлера,
т.е. быть экстремалью интеграла
(1).
общее выражение первой вариации
интеграла (1):
 Эта
первая вариация должна обращаться в
нуль. Член, содержащ интеграл, равен
нулю, поскольку функц
Эта
первая вариация должна обращаться в
нуль. Член, содержащ интеграл, равен
нулю, поскольку функц
 ,
должна и в этом случае удовлетворять
ур-нию Эйлера. Внеинтегральный член
должен обращаться в нуль при
,
должна и в этом случае удовлетворять
ур-нию Эйлера. Внеинтегральный член
должен обращаться в нуль при
 ,
так как этот конец является закреплённым.
Т. о., равенство нулю первой вариации
приводит нас к равенству
,
так как этот конец является закреплённым.
Т. о., равенство нулю первой вариации
приводит нас к равенству
 при
при
 .
На свободном конце
.
На свободном конце
 может быть произвольным, и окончательно
мы получаем на свободном конце след
предельн услов:
может быть произвольным, и окончательно
мы получаем на свободном конце след
предельн услов:
 Оно
даёт нам некоторую связь между
Оно
даёт нам некоторую связь между
 и
и
 на свободн конце. Нетрудно проверить,
что для интеграла (1) условие (2) будет
иметь вид
на свободн конце. Нетрудно проверить,
что для интеграла (1) условие (2) будет
иметь вид
 ,
т.е. в случае интеграла (1) оно сводится
к требованию, чтобы на конце
,
т.е. в случае интеграла (1) оно сводится
к требованию, чтобы на конце
 экстремаль была перпендикулярна к
прямой
экстремаль была перпендикулярна к
прямой
 .
Предельное условие (2) называется
обычно естественным
предельным
или граничным
условием.
.
Предельное условие (2) называется
обычно естественным
предельным
или граничным
условием.
 или
или
 ,
параллельн оси
,
параллельн оси
 .
Положим теперь, что он может перемещаться
по любой заданной линии
.
Положим теперь, что он может перемещаться
по любой заданной линии
 на плоск
на плоск
 .
Для определённости будем считать, что
лев конец
.
Для определённости будем считать, что
лев конец
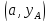 закреплён, а правый может перемещаться
по
закреплён, а правый может перемещаться
по
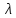 .
Рассуждая, как в Билете 5, докажем, что
если некотор кривая
.
Рассуждая, как в Билете 5, докажем, что
если некотор кривая
 даёт экстремум интегралу, то она должна
удовлетвор ур-нию Эйлера, т.е. быть
экстремалью. Первая вариац должна
обращаться в нуль: слагаемое, содержащ
знак интеграла, будет равно нулю в
силу ур-ния Эйлера, а внеинтегральный
член при
даёт экстремум интегралу, то она должна
удовлетвор ур-нию Эйлера, т.е. быть
экстремалью. Первая вариац должна
обращаться в нуль: слагаемое, содержащ
знак интеграла, будет равно нулю в
силу ур-ния Эйлера, а внеинтегральный
член при
 будет равен нулю в силу условия
закрепления конца. Т. о., равенство
нулю первой вариации приводит нас к
следующ услов на подвижном конце:
будет равен нулю в силу условия
закрепления конца. Т. о., равенство
нулю первой вариации приводит нас к
следующ услов на подвижном конце:
 где
где
 и
и
 – проекции на коорд оси бесконечно
малого перемещен вдоль кривой
– проекции на коорд оси бесконечно
малого перемещен вдоль кривой
 .
Если бы мы считали оба конца подвижными,
то получили бы на обоих концах предельн
условие (1). Достаточно повторить
предыдущ рассужден, помня, что если
кривая даёт экстремум интегралу при
подвижн концах, то тем более она даёт
экстремум при неподвижн концах или
при неподвижн одном конце.
.
Если бы мы считали оба конца подвижными,
то получили бы на обоих концах предельн
условие (1). Достаточно повторить
предыдущ рассужден, помня, что если
кривая даёт экстремум интегралу при
подвижн концах, то тем более она даёт
экстремум при неподвижн концах или
при неподвижн одном конце. угловой коэфт касательной к кривой
угловой коэфт касательной к кривой
 ,
можем переписать услов (1) в виде:
,
можем переписать услов (1) в виде:
 т.
о. это условие, называемое обычно
условием
трансверсальности,
устанавливает связь между угловым
коэф
т.
о. это условие, называемое обычно
условием
трансверсальности,
устанавливает связь между угловым
коэф
 касательной к экстремали и угловым
коэф
касательной к экстремали и угловым
коэф
 касательной к кривой
касательной к кривой
 в каждой точке этой кривой. Если ур-ние
в каждой точке этой кривой. Если ур-ние
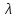 задано в неявной форме
задано в неявной форме
 ,
то условие трансверсальности может
быть переписано в виде:
,
то условие трансверсальности может
быть переписано в виде:
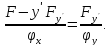
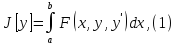 Рассм
сначала функционал вида:
Рассм
сначала функционал вида:
 причём
искомая экстремаль должна проходить
через точки
причём
искомая экстремаль должна проходить
через точки
 и
и
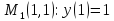 .
Для любой такой кривой функционал (2)
будет положит. Построим линию, состоящиз
двух отрезков прямых линий и соединяющую
точки
.
Для любой такой кривой функционал (2)
будет положит. Построим линию, состоящиз
двух отрезков прямых линий и соединяющую
точки
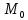 и
и
 ,
а именно, образуем ломанную линию
,
а именно, образуем ломанную линию
 ,
проходящ через нач коорд (т. O)
плоскости
,
проходящ через нач коорд (т. O)
плоскости
 .
функционал (2) для взятой ломаной линии
обращается в нуль, так как вдоль отрезка
.
функционал (2) для взятой ломаной линии
обращается в нуль, так как вдоль отрезка
 ,
а вдоль отрезка
,
а вдоль отрезка
 .
Эта ломаная линия, имеющая угловую
точку в начале координат, будет давать
экстремум интегралу (2).
.
Эта ломаная линия, имеющая угловую
точку в начале координат, будет давать
экстремум интегралу (2). и
и
 и имеющая одну угловую точку
и имеющая одну угловую точку
 ,
даёт экстремум функционалу (1) по
сравнению с другими, к ней достаточно
близкими кривыми, котор также могут
иметь углов точку и должны проходить
через заданные точки
,
даёт экстремум функционалу (1) по
сравнению с другими, к ней достаточно
близкими кривыми, котор также могут
иметь углов точку и должны проходить
через заданные точки
 и
и
 .
можем считать закреплёнными не только
конечные точки, но и точку
.
можем считать закреплёнными не только
конечные точки, но и точку
 ,
котор явл углов точкой для исследуем
кривой. Эта кривая при этом предположении
тем более должна давать экстремум
интегралу (1). Отсюда следует, что
участки кривой, соответствующ
промежуткам
,
котор явл углов точкой для исследуем
кривой. Эта кривая при этом предположении
тем более должна давать экстремум
интегралу (1). Отсюда следует, что
участки кривой, соответствующ
промежуткам
 и
и
 оси
оси
 ,
должны являться экстремалями задачи,
т.е. должны удовлетв соответств ур-нию
Эйлера. Определим вариацию интеграла
(1), приняв нашу кривую за исходную и
разбивая весь промежуток
,
должны являться экстремалями задачи,
т.е. должны удовлетв соответств ур-нию
Эйлера. Определим вариацию интеграла
(1), приняв нашу кривую за исходную и
разбивая весь промежуток
 на две части
на две части
 и
и
 .
.
 и
и
 ,
получаем следующ два условия, котор
должны выполняться в угловой точке
нашей кривой, если эта кривая даёт
экстремум интегралу (1):
,
получаем следующ два условия, котор
должны выполняться в угловой точке
нашей кривой, если эта кривая даёт
экстремум интегралу (1):
 Эти
услов наз
услов Вейерштрасса-Эрдмана.
Эти
услов наз
услов Вейерштрасса-Эрдмана. и
и
 в той точке
в той точке
 ,
в котор
,
в котор
 имеет скачок. Эти выраж будут непрерывными
в остальных точках, где
имеет скачок. Эти выраж будут непрерывными
в остальных точках, где
 - непрерывна. Положим, что нам удалось
построить общий интеграл ур-ния Эйлера.
Значения двух произвольн постоянн,
входящих в этот интеграл, будут, вообще
говоря, различными для промежутков
- непрерывна. Положим, что нам удалось
построить общий интеграл ур-ния Эйлера.
Значения двух произвольн постоянн,
входящих в этот интеграл, будут, вообще
говоря, различными для промежутков
 и
и
 .
Пусть
.
Пусть
 -
общий интеграл для промежутка
-
общий интеграл для промежутка
 и
и
 -
для промежутка
-
для промежутка
 надо
определить пять постояннх, а именно
значен произвольн постоян
надо
определить пять постояннх, а именно
значен произвольн постоян
 и абсциссу (значение
и абсциссу (значение
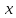 )
)
 точки излома. имеем два предельных
услов при
точки излома. имеем два предельных
услов при
 и
и
 ,
а также два услов (3). Недостающее пятое
равенство мы получим из услов
непрерывности кривой при
,
а также два услов (3). Недостающее пятое
равенство мы получим из услов
непрерывности кривой при
 :
:
