
Bilety_matan_2013
.docx|
Термин “Эконом”. Хар-ка факт-ов произв-ва. Терм “Эк” появился еще в Древней Греции. Это сочетание двух слов :”ойкос”- дом, хозяйство и “комос”- закон. Буквально этот термин переводится как “домоводство”. “Экономика”- это нечто связанное с производством благ (матер и нематер, т.е. не имеющих вещную форму). Во-вторых “Эк” возникает не просто из произв-ва, а из общественного произв-ва, т.е. произв-ва по поводу которого люди вступают в общение друг с другом. И наконец, в-третьих, чтобы что-то произвести, осуществить процесс пр-ва необходимы определенные ресурсы. Те ресурсы, кот необх для осуществления процесса пр-ва, наз факторами производства. К ним относятся : - природные ресурсы, т.е. все естественные ресурсы (“даровые” блага) природы, используемые в производстве - земля, леса, воздух, вода, полезные ископаемые, любое добываемое в природе сырье; -труд - совокупность знаний, умений, навыков, физических и интеллектуальных способностей человека, т.е. рабочая сила, которую он пускает в ход для производства благ (продукции); - капитал - (инвестиционные ресурсы)- все средства производства произведенные человеком- здания, сооружения, машины, оборудование, полуфабрикаты, инструменты и т.д., а также денежные средства (“инвестирование”- процесс производства и накопления средств производства). - предпринимательская способность- т.е. способность объединить в едином процессе первые три фактора производства, способность принимать решения и рисковать в этом процессе. Экономика исследует проблемы эффективного использования ограниченных производственных ресурсов или управления ими с целью достижения максимального удовлетворения потребностей человека (цель потребителя- максимальное удовлетв. потребностей). - “рыночная экономика” - система, форма организации хозяйства, при которой производитель и потребитель свободны в связях между собой и связываются по экономическим мотивам ( посредством рынка), через систему цен, спроса, предложения, прибылей, убытков, конкуренции решают “что-как-для кого производить”; - смешанная экономика - предполагает определенное вмешательство государства в систему “рыночной экономики” Экономическая политика, т.е. нормативное (основанное на определенных методиках, положениях, законах) экономическое поведение индивидумов и сообществ индивидумов. Дедукт - движение от теории к фактам индукт - от фактов к теории
|
Билет 2. Интегрир и дифференц оригиналов и изображ. Свёртка функц, её изображ. Интегрирование и дифференц оригиналов и изображ относятся к свойствам преобразования Лапласа. Дифференцирование
оригинала. Если
функции
Дифференцирование
изображения. Дифференцирование
изображения сводится к умножению на
Интегрирование
оригинала. Интегрирование
оригинала сводится к делению изображения
на
Интегрирование
изображения. Если
интеграл
Теорема
умножения (теорема о свёртке).
Произведение
двух изображений
|
Билет 3. Ф-ла Дюамеля. Применение преобразов Лапласа к реш диф ур. Если
функция
То
Это – так называемая формула Дюамеля. Пусть
требуется решить линейное дифференциальное
уравнение с постоянными коэффициентами
-го порядка
с
той же левой частью и правой частью,
равной единице при условиях (3). Переходя
к операторным уравнениям, будем иметь
(
для
(4). Из (5) находим
Учитывая,
что
|
|
Билет 3(продолжение )Примен преобраз Лапласа для решения диф ур и сист диф ур процесс реш ДУ или сист ДУ сводится к переводу оригиналов уравнений в эквивалентные изображения этих уравнений, а затем нахождения изображений неизвестных переменн, после чего найденные изображ переводятся обратно в оригиналы. При этом используются св-ва преобразов Лапласа о дифференцировании. Интегралы Френеля
Обращение
преобразов Лапласа. Обратное
преобраз Лапласа
Теорема
обращения. Пусть
Теорема
разложения. Если
|
Билет 4. Классич зад вариац исчислен (задача Дидоны, задача о брахистохроне и т.д.). Дифф-ное исчисление в нормированных пространствах (диф-лы Гато и Фреше). Необходимое услов экстремума функционала. Лемма Лагранжа. Лемма Дюбуа-Реймона.
Зада́ча Дидо́ны — исторически первая задача вариационного исчисления. Связана с древней легендой об основании города Карфагена.
Задача
сводится к нахождению экстремума функционала
с
граничными условиями
Задача о брахистохроне Среди плоских кривых, соединяющих две данные точки А и В, лежащих в одной вертикальной плоскости (В ниже А), найти ту, двигаясь по которой под действием только силы тяжести, сонаправленной с отрицательной полуосью OY, материальная точка достигнет В из А за кратчайшее время Пусть имеются две произвольные точки, расположенные на разных ординатах. Далее пусть произвольная материальная точка M скатывается от точки A к точке B под действием только силы тяжести (силы трения отсутствуют). Найдем такую траекторию, при которой время скатывания будет минимально. Направим ось ординат вниз и сопоставим начальной точке нулевое значение ординаты. Запишем закон сохранения энергии для материальной точки M:
Получаем:
откуда
можно найти значение проекции скорости
на ось
Поскольку
время на спуск равняется
|
|

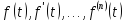 являются
функциями-оригиналами, и
являются
функциями-оригиналами, и
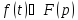 ,
то
,
то
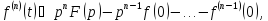 где
под
где
под
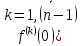 понимается
понимается
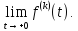
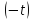 оригинала
оригинала

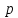 ,
то есть если
,
то есть если
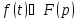 ,
то
,
то

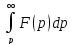 сходится,
то он служит изображением функции
сходится,
то он служит изображением функции
 :
:
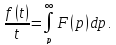
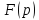 и
и
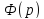 также является изображением, причём
также является изображением, причём
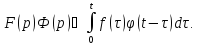 Интеграл
в правой части выражения называется
свёрткой
функций
Интеграл
в правой части выражения называется
свёрткой
функций
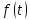 и
и
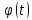 и обозначается символом
и обозначается символом
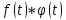 .
. непрерывна на
непрерывна на
 ,
а функция
,
а функция
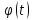 непрерывно дифференцируема на
непрерывно дифференцируема на
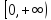 и
и
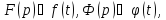
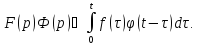 Отсюда
по теореме о дифференцировании
оригинала
Отсюда
по теореме о дифференцировании
оригинала
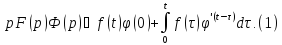
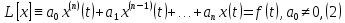 при
нулевых начальных условиях
при
нулевых начальных условиях
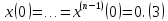 Допустим,
что известно решение уравнения
Допустим,
что известно решение уравнения
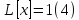
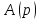 – известный многочлен от
– известный многочлен от
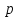 )
)
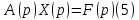 для
(2) и
для
(2) и
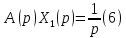
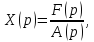 а из (6)
а из (6)
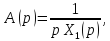 откуда
откуда
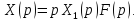 Согласно
формуле (1)
Согласно
формуле (1)
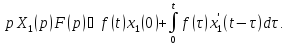
 получаем
получаем
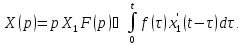 Отсюда
решение
Отсюда
решение
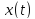 уравнения (2) при нулевых начальных
условиях (3) будет иметь вид
уравнения (2) при нулевых начальных
условиях (3) будет иметь вид
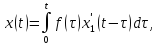 где
где
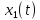 – решение задачи (4)-(3).
– решение задачи (4)-(3).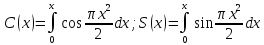
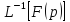 функц
функц
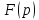 комплексной перемен
комплексной перемен
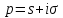 есть функц
есть функц
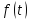 ,
для которой преобраз Лапласа
,
для которой преобраз Лапласа
 есть
есть
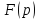 .
Не каждая функция
.
Не каждая функция
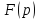 имеет обратное преобразование Лапаласа.
имеет обратное преобразование Лапаласа.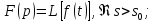 тогда в каждом открытом интервале,
где
тогда в каждом открытом интервале,
где
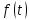 ограничена и имеет конечное число
точек макс, мин и точек разрыва
ограничена и имеет конечное число
точек макс, мин и точек разрыва
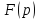 – аналитич функц в окрестн бесконечно
удалённой тчк и равна в ней нулю, и
если лорановское разложение
– аналитич функц в окрестн бесконечно
удалённой тчк и равна в ней нулю, и
если лорановское разложение
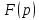 в окрестн бесконеч удалённой точки
имеет вид
в окрестн бесконеч удалённой точки
имеет вид
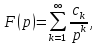 то оригиналом
то оригиналом
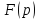 служит функция
служит функция
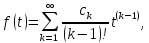 причём
этот ряд сходится при всех
причём
этот ряд сходится при всех
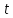 .
.