
matan_2013
.docx|
Билет 1. Понятие об интегр преобразов. Преобразов Лаплпаса. Интегральн преобраз явл мощным средством для решения диф ур и систем диф ур.
Функцией-оригиналом
называется
любая комплекснозначная функция
Для
всех отрицательных
Нижняя
грань
Простейшей
функцией оригиналом является так
называемая единичная функция Хевисайда
Очевидно,
так
что если
Изображением
функции
Тот
факт, что
Функция
Свойство
линейности. Для
любы комплексных постоянных
Теорема
подобия. Для
любого постоянного
Теорема
запаздывания. Если
Теорема
затухания (смещения). Если
|
Билет 2. Интегрир и дифференц оригиналов и изображ. Свёртка функц, её изображ. Интегрирование и дифференц оригиналов и изображ относятся к свойствам преобразования Лапласа. Дифференцирование
оригинала. Если
функции
Дифференцирование
изображения. Дифференцирование
изображения сводится к умножению на
Интегрирование
оригинала. Интегрирование
оригинала сводится к делению изображения
на
Интегрирование
изображения. Если
интеграл
Теорема
умножения (теорема о свёртке).
Произведение
двух изображений
|
Билет 3. Ф-ла Дюамеля. Применение преобразов Лапласа к реш диф ур. Если
функция
То
Это – так называемая формула Дюамеля. Пусть
требуется решить линейное дифференциальное
уравнение с постоянными коэффициентами
-го порядка
с
той же левой частью и правой частью,
равной единице при условиях (3). Переходя
к операторным уравнениям, будем иметь
(
для
(4). Из (5) находим
Учитывая, что
|
|
Билет 3(продолжение )Примен преобраз Лапласа для решения диф ур и сист диф ур процесс реш ДУ или сист ДУ сводится к переводу оригиналов уравнений в эквивалентные изображения этих уравнений, а затем нахождения изображений неизвестных переменн, после чего найденные изображ переводятся обратно в оригиналы. При этом используются св-ва преобразов Лапласа о дифференцировании. Интегралы Френеля
Обращение
преобразов Лапласа. Обратное
преобраз Лапласа
Теорема
обращения. Пусть
Теорема
разложения. Если
|
|
|
|
Билет 4. Классич зад вариац исчислен (задача Дидоны, задача о брахистохроне и т.д.). Зада́ча Дидо́ны — исторически первая задача вариационного исчисления. Связана с древней легендой об основании города Карфагена.
Задача
сводится к нахождению экстремума функционала
с
граничными условиями
Задача о брахистохроне Среди плоских кривых, соединяющих две данные точки А и В, лежащих в одной вертикальной плоскости (В ниже А), найти ту, двигаясь по которой под действием только силы тяжести, сонаправленной с отрицательной полуосью OY, материальная точка достигнет В из А за кратчайшее время Пусть имеются две произвольн точки, располож на разных ординатах. пусть произвольн материальная точка M скатывается от точки A к точке B под действ только силы тяжести. Найдем такую траекторию, при котор время скатывания будет миним. Направим ось ординат вниз и сопоставим начальной точке нулевое значение ординаты. Запишем закон сохранения энергии для материальной точки M:
Получаем:
откуда:
Поскольку
время на спуск равняется Задача о кратчайшем времени прохожден светом пути по заданной траектории
Пусть имеется
неоднородн, изотропн среда, в кажд
точке (x, y, z)
котор определена скорость распространен
света v(x, y, z),
зависящ от изменен по объему преломляющих
св-в среды.
Время распространен света из одной
точки в др явл функц от линии его
распространен и определяется
интегралом
Билет4(продолжение2)
Для
того, чтобы кривая
Пусть
Тогда
|
Билет 4(продолжение1)Диф-ное исчислен в нормированных пространствах Пусть
дан некотор класс
Если
приращ функционала
можно
представить в виде Пусть
где
сходимость понимается как сходимость
по норме в пространстве Дифференциал Фреше
Пусть
Производной
Фреше оператора
причем
для остаточного члена
Если
производная Фреше сущ, то
оператор
Необх
услов экстремума функционала
функционал
Аналогично опр и слаб относит мин функционала.
Макс
и мин (сильн и слаб) функционала
Всякий
сильн экстремум есть в то же время и
слабый, но не наоборот.Экстремум
функционала
|
|
|
|
|
|
Билет 5. Простейшая задача вариационного исчисления. Простейш
задачей вариац исчислен явл нахождение
экстремума для функционала с
фиксированными границами
Принимаем,
что функция
Выведем
необх услов, котор должна подчиняться
При
любом заданном положит
Производя
интегриров по частям, можно написать: Применяя
лемму Дюбуа-Реймона, мы можем утверждать,
что кривая
постоянные,
котор должны определяться из двух
предельных условий ( Раскрывая
полную производную по
Произведение
|
Билет 6. Функционалы от нескольких функций. уравнение
Эйлера для случая, когда функционал
зависит от нескольких функций.Ограничимся
случаем двух функций: Строим
две функции, близкие к
В
силу (2) вариация интеграла (1) выразится
формулой:
Для случая
функционала от
|

 действительного аргумента
действительного аргумента
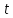 ,
удовлетворяющая условиям:
,
удовлетворяющая условиям: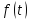 интегрируема на
любом конечном интервале оси
интегрируема на
любом конечном интервале оси
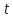 (локально интегрируема);
(локально интегрируема);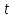 :
: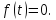
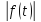 возрастает при
возрастает при
 не быстрее показательной функции,
т.е. существуют такие постоянные
не быстрее показательной функции,
т.е. существуют такие постоянные
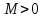 и
и
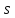 ,
что для всех
,
что для всех
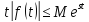
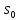 всех чисел
всех чисел
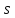 ,
для которых справедливо неравенство
выше, называется показателем роста
функции
,
для которых справедливо неравенство
выше, называется показателем роста
функции
 .
.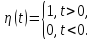

 удовлетворяет условиям 1 и 3, то
удовлетворяет условиям 1 и 3, то
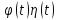 удовлетворяет всем условиям, налагаемым
на функции-оригиналы.
удовлетворяет всем условиям, налагаемым
на функции-оригиналы.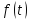 по Лапласу
называется функция
по Лапласу
называется функция
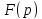 комплексного переменного
комплексного переменного
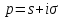 ,
определяемая равенством
,
определяемая равенством
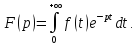
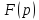 есть изображение
есть изображение
 ,
будем символически записывать так:
,
будем символически записывать так:
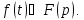
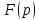 определена в полуплоскости
определена в полуплоскости
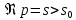 и является в этой полуплоскости
аналитической функцией.
и является в этой полуплоскости
аналитической функцией.
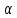 и
и
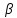
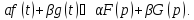 (Здесь
и всюду в дальнейшем считаем
(Здесь
и всюду в дальнейшем считаем
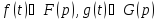 ).
).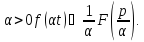
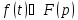 ,
то для любого положительного
,
то для любого положительного
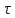
 Теорему
запаздывания удобно использовать при
отыскании изображения функций, которые
на разных участках задаются разными
аналитическими выражениями.
Теорему
запаздывания удобно использовать при
отыскании изображения функций, которые
на разных участках задаются разными
аналитическими выражениями.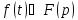 ,
то для любого комплексного
,
то для любого комплексного
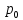

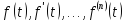 являются
функциями-оригиналами, и
являются
функциями-оригиналами, и
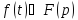 ,
то
,
то
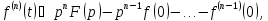 где
под
где
под
 понимается
понимается

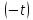 оригинала
оригинала

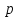 ,
то есть если
,
то есть если
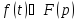 ,
то
,
то
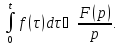
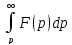 сходится,
то он служит изображением функции
сходится,
то он служит изображением функции
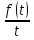 :
:
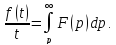
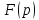 и
и
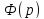 также является изображением, причём
также является изображением, причём
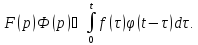 Интеграл
в правой части выражения называется
свёрткой
функций
Интеграл
в правой части выражения называется
свёрткой
функций
 и
и
 и обозначается символом
и обозначается символом
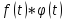 .
. непрерывна на
непрерывна на
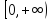 ,
а функция
,
а функция
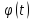 непрерывно дифференцируема на
непрерывно дифференцируема на
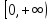 и
и
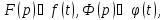
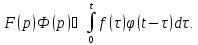 Отсюда
по теореме о дифференцировании
оригинала
Отсюда
по теореме о дифференцировании
оригинала
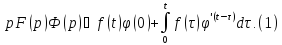
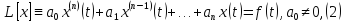 при
нулевых начальных условиях
при
нулевых начальных условиях
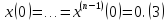 Допустим,
что известно решение уравнения
Допустим,
что известно решение уравнения

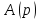 – известный многочлен от
– известный многочлен от
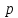 )
)
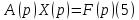 для
(2) и
для
(2) и
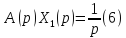
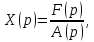 а из (6)
а из (6)
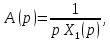 откуда
откуда
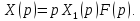 Согласно
формуле (1)
Согласно
формуле (1)
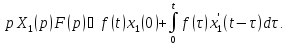
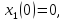 получаем
получаем
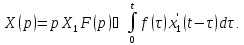 Отсюда
решение
Отсюда
решение
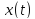 уравнения (2) при нулевых начальных
условиях (3) будет иметь вид
уравнения (2) при нулевых начальных
условиях (3) будет иметь вид
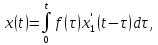 где
где
 – решение задачи (4)-(3
– решение задачи (4)-(3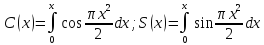
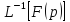 функц
функц
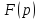 комплексной перемен
комплексной перемен
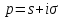 есть функц
есть функц
 ,
для которой преобраз Лапласа
,
для которой преобраз Лапласа
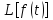 есть
есть
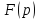 .
Не каждая функция
.
Не каждая функция
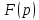 имеет обратное преобразование Лапаласа.
имеет обратное преобразование Лапаласа.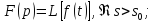 тогда в каждом открытом интервале,
где
тогда в каждом открытом интервале,
где
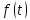 ограничена и имеет конечное число
точек макс, мин и точек разрыва
ограничена и имеет конечное число
точек макс, мин и точек разрыва
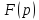 – аналитич функц в окрестн бесконечно
удалённой тчк и равна в ней нулю, и
если лорановское разложение
– аналитич функц в окрестн бесконечно
удалённой тчк и равна в ней нулю, и
если лорановское разложение
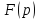 в окрестн бесконеч удалённой точки
имеет вид
в окрестн бесконеч удалённой точки
имеет вид
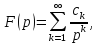 то оригиналом
то оригиналом
 служит функция
служит функция
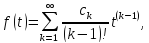 причём
этот ряд сходится при всех
причём
этот ряд сходится при всех
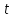 .
.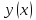 давала экстремум функционалу
давала экстремум функционалу
 ,
необходимо, чтобы данная кривая
удовлетворяла диф ур Эйлера:
,
необходимо, чтобы данная кривая
удовлетворяла диф ур Эйлера: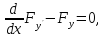 где
где
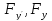 – частн производн от функц
– частн производн от функц
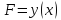 ,
задающей кривую.
Лемма
Лагранжа
Если
интеграл
,
задающей кривую.
Лемма
Лагранжа
Если
интеграл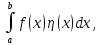 где
где
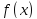 – фиксир непрерывн в промежутке
– фиксир непрерывн в промежутке
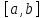 функц, обращается в нуль для всякой
функц
функц, обращается в нуль для всякой
функц
 ,
непрерывн вместе со своей производн
и равной нулю на концах
,
непрерывн вместе со своей производн
и равной нулю на концах
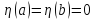 ,
то
,
то
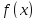 тождественно равна нулю в промежутке
тождественно равна нулю в промежутке
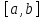 .
Лемма
Дюбуа-Реймона
.
Лемма
Дюбуа-Реймона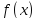 и
и
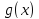 непрерывны на
непрерывны на
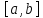 и для любой бесконечно диф-мой на
и для любой бесконечно диф-мой на
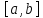 функц
функц
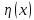 ,
непрерывн вместе со своей производн
и равной нулю на концах
,
непрерывн вместе со своей производн
и равной нулю на концах
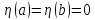 ,
выполнено равенство
,
выполнено равенство
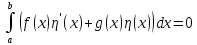
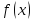 непрерывно диф-ма на
непрерывно диф-ма на
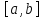 ,
и
,
и
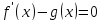 на
на
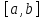 .
. функц
функц
 .
Если кажд функц
.
Если кажд функц
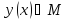 по некотор закону поставлено в соотв
определённое число
по некотор закону поставлено в соотв
определённое число
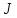 ,
то говорят, что в классе
,
то говорят, что в классе
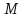 определён функционал
определён функционал
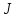 ,
и пишут
,
и пишут
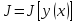 .
Класс
.
Класс
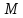 функций
функций
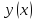 ,
на котор определён функционал
,
на котор определён функционал
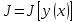 ,
назыв областью
задания функционала.
,
назыв областью
задания функционала.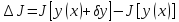
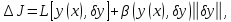 где
где
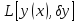 –
линейный по отношен к
–
линейный по отношен к
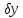 функционал и
функционал и
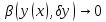 при
при
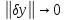 ,
то линейная по отнош к
,
то линейная по отнош к
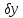 часть приращ функционала, т.е.
часть приращ функционала, т.е.
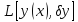 ,
называется вариацией
функционала
,
называется вариацией
функционала
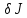 .
В этом случ функционал
.
В этом случ функционал
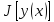 наз дифференцируемым
в точке
наз дифференцируемым
в точке
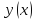 .
Дифференциал
Гато (слабый дифференциал)
.
Дифференциал
Гато (слабый дифференциал)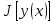 достигает на кривой
достигает на кривой
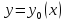 макс, если знач функционала
макс, если знач функционала
 на любой близкой к
на любой близкой к
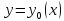 кривой не больше чем
кривой не больше чем
 ,
т.е.
,
т.е.
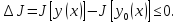 Если
Если
 ,
причём
,
причём
 ,
только при
,
только при
 ,
то говорят, что на кривой
,
то говорят, что на кривой
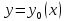 достигается строгий макс. Аналогично
определ кривая
достигается строгий макс. Аналогично
определ кривая
 ,
на котор реализ миним. В этом случ
,
на котор реализ миним. В этом случ
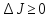 на всех кривых, близких к кривой
на всех кривых, близких к кривой
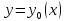 .
функционал
.
функционал
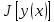 достигает на кривой
достигает на кривой
 сильного
относит макс,
если для всех допустим кривых
сильного
относит макс,
если для всех допустим кривых
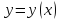 ,
располож в некотор
,
располож в некотор
 -окрестн
нулевого порядка кривой
-окрестн
нулевого порядка кривой
 ,
имеем
,
имеем
 Аналогично
определяется и сильный
относит мин функционала.
Аналогично
определяется и сильный
относит мин функционала.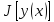 достигает слаб
относитмакс,
если для всех допустим кривых
достигает слаб
относитмакс,
если для всех допустим кривых
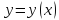 ,
располож в некотор
,
располож в некотор
 -окрестности
первого порядка кривой
-окрестности
первого порядка кривой
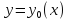 ,
имеем
,
имеем
 называют относит
экстремумами.
называют относит
экстремумами.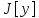 на всей совокупности функций, на
которых он определён, называется
абсолютным
экстремумом.Всякий
абс экстремум явл слаб и сильн относит
экстремумом, но не всякий относит
экстремум будет абсолютн.
на всей совокупности функций, на
которых он определён, называется
абсолютным
экстремумом.Всякий
абс экстремум явл слаб и сильн относит
экстремумом, но не всякий относит
экстремум будет абсолютн.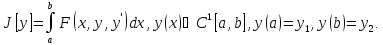
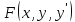 и её производные непрерывны на
и её производные непрерывны на
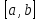 .
.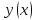 для того, чтобы функционал
для того, чтобы функционал
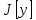 имел экстремум. Возьмём любую функц
имел экстремум. Возьмём любую функц
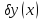 ,
равную нулю на концах промежутка
интегрир, и наряду с
,
равную нулю на концах промежутка
интегрир, и наряду с
 ,
котор должна давать экстремум
функционалу
,
котор должна давать экстремум
функционалу
 ,
образуем новую функц
,
образуем новую функц
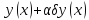 ,
где
,
где
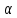 – малый численный параметр. Эта новая
функция удовлетв тем же предельным
услов, что и
– малый численный параметр. Эта новая
функция удовлетв тем же предельным
услов, что и
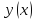 .
Подставив её в функционал
.
Подставив её в функционал
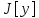 ,
получим в рез-те интегриров некотор
функц параметра
,
получим в рез-те интегриров некотор
функц параметра
 :
:
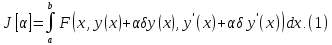
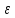 функция
функция
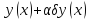 находится в
находится в
 -окрестности
(даже первого порядка) линии
-окрестности
(даже первого порядка) линии
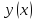 для всех значен парам
для всех значен парам
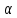 ,
достаточно близких к нулю. Следов, раз
,
достаточно близких к нулю. Следов, раз
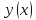 даёт экстремум функционалу
даёт экстремум функционалу
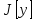 ,
то функция (1) должна иметь экстремум
при значении
,
то функция (1) должна иметь экстремум
при значении
 ,
а потому её произвя должна обратиться
в нуль при
,
а потому её произвя должна обратиться
в нуль при
 .
Диф-руя под знаком интегр и обозначая
частн производн индексами, будем
иметь:
.
Диф-руя под знаком интегр и обозначая
частн производн индексами, будем
иметь: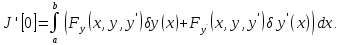
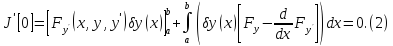
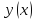 ,
дающая экстремум исходному функционалу,
должна удовл след диф ур:
,
дающая экстремум исходному функционалу,
должна удовл след диф ур:
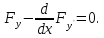 Данное
диф урназ уравнением Эйлера. Оно
представляет собой диф ур второго
порядка, и его общий интеграл содержит
две произвольные Билет 5(продолжение)
Данное
диф урназ уравнением Эйлера. Оно
представляет собой диф ур второго
порядка, и его общий интеграл содержит
две произвольные Билет 5(продолжение)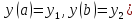 .
.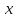 ,
мы можем написать это уравнение в
виде:
,
мы можем написать это уравнение в
виде:
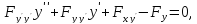 где,
например,
где,
например,
 есть частная производная второго
порядка, взятая по
есть частная производная второго
порядка, взятая по
 и
и
 .
.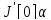 ,
являющееся дифференциалом функции
,
являющееся дифференциалом функции
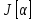 при
при
 ,
наз обычно первой вариацией исходного
функционала
,
наз обычно первой вариацией исходного
функционала
 .
Принимая во внимание (2), можем написать:
.
Принимая во внимание (2), можем написать:
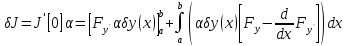

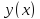 и
и
 :
:
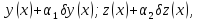 где
где
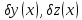 – произвольн функц, равн нулю на концах
промежутка
– произвольн функц, равн нулю на концах
промежутка
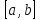 .
Подставляя их в интеграл (1), получ
функц
.
Подставляя их в интеграл (1), получ
функц
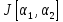 от
от
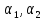 ,
и для того, чтобы к
,
и для того, чтобы к
 и
и
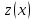 давали экстремум функционалу (1), необх,
чтобы частн производн от
давали экстремум функционалу (1), необх,
чтобы частн производн от
 по
по
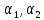 обращались в нуль при
обращались в нуль при
 .
Производя вычислен, аналогичные
вычислениям для функционала от одной
функц, получ для этих частн производн
след выраж:
.
Производя вычислен, аналогичные
вычислениям для функционала от одной
функц, получ для этих частн производн
след выраж: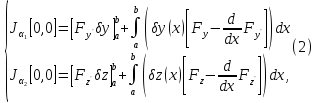 и
так как внеинтегральные члены обращаются
в нуль, то, как и в случ с функционалом
от одной функц, мы убедимся в том, что
для того, чтобы функц
и
так как внеинтегральные члены обращаются
в нуль, то, как и в случ с функционалом
от одной функц, мы убедимся в том, что
для того, чтобы функц
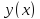 и
и
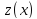 давали экстремумы функционалу (1),
необх, чтобы они удовлетв следующей
сист двух ур-ний второго порядка:
давали экстремумы функционалу (1),
необх, чтобы они удовлетв следующей
сист двух ур-ний второго порядка:
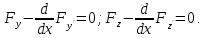 Кроме
этих уравн мы имеем ещё и предельные
условия:
Кроме
этих уравн мы имеем ещё и предельные
условия: выражающие
закрепление концов искомой
пространственной кривой.
выражающие
закрепление концов искомой
пространственной кривой.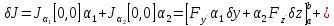

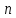 функций вычисления производятся
аналогично.
функций вычисления производятся
аналогично.