Физика 3 семестр / новая папка / Помощь к экзамену / Темы / 06.Теорема Гаусса

1.6. Теорема Остроградского–Гаусса для электростатического поля в вакууме

Основная теорема электростатики была выведена в 1829 г. русским математиком М.В. Остроградским для произвольного векторного поля. Немецкий физик и математик К.Ф. Гаусс в 1830г. применил ее к расчету электростатических полей.

Проведем в электрическом поле произвольную поверхность площадью S (рис.1.15). Назовем элементарным потоком напряженности электростатического поля через малый участок (элемент) поверхности S величину

, (1.20)

где – вектор площади элемента поверхности, – вектор единичной нормали к поверхности в месте расположения элемента . Справедливы соотношения: ; . Малый элемент поверхности выбирается таких размеров, чтобы в его пределах можно было считать поле однородным, а кривизну поверхности можно было бы не учитывать.

Поток вектора напряженности электростатического поля через всю поверхность S находится как алгебраическая сумма потоков сквозь все малые участки этой поверхности:

. (1.21)

При вычислении (1.21) договоримся направлять все векторы в одну и ту же сторону по отношению к поверхности S. Например, в случае замкнутой поверхности S в дальнейшем будем считать векторы внешними нормалями, т.е. направленными из области, ограниченной этой поверхностью.

Из (1.21) видно, что Ф = 0, если во всех точках поверхности S силовые линии поля перпендикулярны векторам , т.е. “скользят” по поверхности. С другой стороны, поток максимален, если поверхность S расположена перпендикулярно силовым линиям в каждой точке пространства. Таким образом, поток вектора напряженности через поверхность пропорционален числу силовых линий, пересекающих эту поверхность.

Вспомним из математики понятие телесного угла. Это часть пространства, ограниченная прямыми, проведенными из одной точки (вершины угла) ко всем точкам замкнутой кривой (рис.1.16). Мерой телесного угла является отношение площади элемента , вырезаемого конической поверхностью угла на сфере радиуса r с центром в вершине угла, к квадрату радиуса:

.

Единицей телесного угла в СИ служит угол, опирающийся на сферу радиусом 1 м и вырезающий на ней элемент площадью 1 м². Такой телесный угол равен 1 стерадиан (обозначается 1 ср). Поскольку площадь поверхности всей сферы равна , то телесный угол, опирающийся на всю сферу и охватывающий все пространство, равен ср.

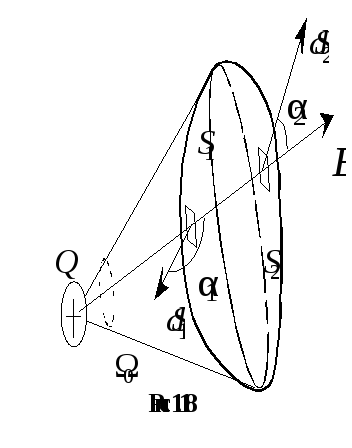
Рассмотрим точечный заряд Q, охваченный произвольной замкнутой поверхностью (рис.1.17). Выделим на этой поверхности элемент площадью , “вырезаемый” из нее телесным углом с вершиной в заряде. Элементарный поток вектора напряженности поля точечного заряда через элемент , согласно (1.20), в СИ равен

.

Тогда полный поток вектора напряженности через всю замкнутую поверхность можно найти как

. (1.22)

Кружок на значке интеграла означает, что суммирование производится по замкнутой поверхности. Если произвольная замкнутая поверхность охватывает точечные заряды , то можно составить систему уравнений:

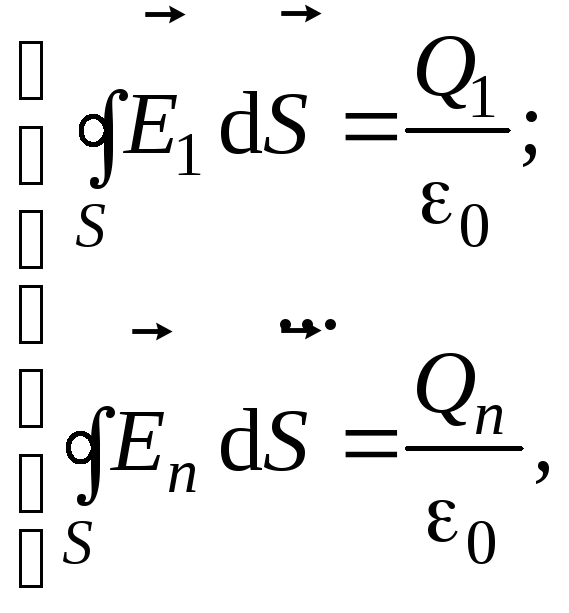
где – напряженность поля каждого из зарядов. Складывая уравнения системы, получим

. (1.23)

Итак, если внутри замкнутой поверхности находятся электрические заряды, то поток вектора напряженности пропорционален сумме этих зарядов.

Рассмотрим теперь точечный заряд , расположенный вне произвольной замкнутой поверхности (рис.1.18). В этом случае касательная коническая поверхность с вершиной в точке расположения заряда разбивает поверхность S на две части: и . Полный поток напряженности через всю поверхность S равен алгебраической сумме потоков через эти части:

.

Однако если для всех элементов поверхности углы между векторами и внешними нормалями тупые (при , то для всех элементов поверхности эти углы острые. Следовательно,

, .(1.24)

Поскольку поверхности и видны из точки расположения заряда Q под одним и тем же телесным углом , то, согласно (1.22),

.

Отсюда, с учетом (1.24), получаем

. (1.25)

Обобщим выводы (1.22), (1.23), (1.25). Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность пропорционален алгебраической сумме зарядов, охваченных этой поверхностью:

. (1.26)

Полученное соотношение выражает теорему Остроградского–Гаусса для электростатического поля в вакууме. Замкнутую поверхность S, фигурирующую в теореме, часто называют гауссовой поверхностью. Отметим, что коэффициент пропорциональности между потоком напряженности и суммой зарядов, охваченных этой поверхностью, определяется выбором системы единиц физических величин. В СИ этот коэффициент равен (см. 1.2). В других системах единиц он может быть другим.

1.7. Примеры использования теоремы Остроградского–Гаусса

Применение теоремы Остроградского–Гаусса (1.26) особенно удобно для расчета электростатических полей симметричных систем зарядов. В этом случае можно так выбрать гауссову поверхность, что поток напряженности поля через нее легко выражается через искомое значение модуля вектора . Решение задачи о нахождении напряженности поля в какой-либо точке пространства должно осуществляться следующим образом:

1. Исходя из симметрии распределения заданной системы зарядов в пространстве необходимо построить силовые линии поля, т.е. определить направление вектора в любой точке пространства.

2. Выбрать “удобную” замкнутую гауссову поверхность, отвечающую следующим требованиям:

а) она должна проходить через исследуемую точку;

б) площадь поверхности должна быть известна;

в) модуль напряженности поля должен быть постоянен в точках всей поверхности или хотя бы ее части;

г) угол между и внешней нормалью к поверхности должен быть известен в любой точке поверхности (это обеспечивается выполнением п. 1).

3. Определить поток напряженности поля через выбранную поверхность. Если выполнено условие п.2в, то

,

где – постоянный модуль напряженности поля во всех точках части поверхности .

4. Определить алгебраическую сумму зарядов, охваченных поверхностью S.

5. Применить теорему, т.е. приравнять результаты, полученные в пп.3 и 4 с учетом коэффициента пропорциональности.