
Физика 3 семестр / новая папка / Помощь к экзамену / Темы / 31.система уравнений Максвелла
.doc8.5. Система уравнений Максвелла
в дифференциальной форме
Запишем систему уравнений Максвелла (8.5) в дифференциальном виде, объединив (8.10), (8.9), (8.6) и (8.7):

(8.14)
Развернем эти уравнения, использовав полученные соотношения для ротора и дивергенции.
 (8.15)
(8.15)
Следует отметить, что уравнения в интегральной форме имеют бóльшую общность, чем в дифференциальной форме, т.к. они остаются справедливыми и тогда, когда в пространстве можно выбрать поверхности, на которых свойства среды или полей меняются скачком. Дифференциальные же уравнения предполагают непрерывность величин, входящих в них. Для использования дифференциальных уравнений дополним их граничными условиями
 (8.16)
(8.16)
которые справедливы и для стационарных, и для переменных электрических и магнитных полей.
Системы (8.14) недостаточно для описания полей, даже при наличии заданного распределения зарядов и токов проводимости, т.к. в системе уравнений отсутствуют особенности среды, в которой рассматриваются поля. С этой целью дополним систему еще тремя уравнениями, которые верны для слабых полей и для медленно меняющихся во времени и в пространстве полей:
 (8.17)
(8.17)
Итак, рассмотрев систему уравнений Максвелла, мы получили такой вывод: переменное электрическое поле возбуждает вихревое магнитное (2-е уравнение), переменное магнитное возбуждает вихревое электрическое (1-е уравнение), и т.д. Таким образом, если возбудить с помощью колеблющихся зарядов переменное электрическое поле, то в окружающем их пространстве возникают взаимные превращения электрического и магнитного полей. Именно эта совокупность последовательно сменяющих друг друга в пространстве электрического и магнитного полей и называется электромагнитным полем.
Поскольку простейший способ его получения – колебания электрических зарядов, то следующий раздел мы посвятим электромагнитным колебаниям.
9. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
Колебаниями называются процессы (движения или изменения состояния), в той или иной степени повторяющиеся во времени. В зависимости от природы колебательного процесса и “механизма” его возбуждения различают: механические колебания (колебания маятников, струн, частей машин, мостов и других сооружений, давления воздуха при распространении в нем звука и т.п.); электромагнитные колебания (колебания переменного электрического тока в цепи, колебания векторов напряженности электрического и магнитного поля); электромеханические колебания (колебания мембраны телефона) и пр. Система, совершающая колебания, называется колебательной системой.
Важно, что независимо от природы колебаний и характера колебательной системы все колебательные процессы подчиняются одним и тем же закономерностям. Основные выводы, полученные нами при рассмотрении механических колебаний (см. гл.5 первой части курса), справедливы и для электромагнитных колебательных процессов. Это касается дифференциальных уравнений колебаний, их решений, определения характеристик собственных, затухающих и вынужденных колебаний. Поэтому при анализе электромагнитных колебаний мы будем использовать выводы и соотношения, полученные ранее.
9.1. Собственные колебания
в последовательном колебательном контуре

свободные незатухающие колебания заряда конденсатора и тока в катушке. Рассмотрим процесс возникновения колебаний подробнее.
На
рис. 9.1, а
показано исходное состояние системы.
Конденсатор заряжен максимальным
зарядом
![]() ,
где
,
где
![]() – выходное напряжение источника, которым
проводилась зарядка конденсатора. Между
обкладками конденсатора в этом состоянии
существует электрическое поле, энергия
которого равна
– выходное напряжение источника, которым
проводилась зарядка конденсатора. Между
обкладками конденсатора в этом состоянии
существует электрическое поле, энергия
которого равна
![]() .
Если конденсатор подключить к катушке,
то он начнет разряжаться и в контуре
возникнет электрический ток. В результате
энергия электрического поля будет
уменьшаться, но зато появится все
увеличивающаяся энергия магнитного
поля, обусловленного током через катушку.
В момент, когда сила тока в цепи равна
i,
энергия магнитного поля составит
.
Если конденсатор подключить к катушке,
то он начнет разряжаться и в контуре
возникнет электрический ток. В результате
энергия электрического поля будет
уменьшаться, но зато появится все
увеличивающаяся энергия магнитного
поля, обусловленного током через катушку.
В момент, когда сила тока в цепи равна
i,
энергия магнитного поля составит
![]() .
.
Поскольку
активное сопротивление контура равно
нулю, то полная энергия системы, состоящая
из энергий электрического и магнитного
полей, не расходуется на нагревание
проводов и остается постоянной. Поэтому
в тот момент, когда конденсатор полностью
разряжается, т.е. его заряд (а значит, и
энергия электрического поля) обращается
в нуль, энергия магнитного поля, а значит
и сила тока в цепи, достигают наибольшего
значения:
![]() (рис. 9.1, б).
Происходит это за счет возникновения
в контуре ЭДС самоиндукции. Т.к. при
разрядке конденсатора сила тока в цепи
изменяется, то возникающая самоиндукция
стремится поддержать силу тока в цепи
неизменной. В результате, когда конденсатор
полностью разряжен, ЭДС самоиндукции
поддерживает ток в цепи в том же
направлении. Поскольку направление
тока – это условное направление движения
положительных зарядов в цепи, то
конденсатор заряжается так, что знаки
зарядов обкладок противоположны
исходному состоянию (рис.9.1, в).
При этом сила тока в цепи уменьшается,
энергия электрического поля конденсатора
растет. Когда заряд конденсатора
достигает прежнего максимального
значения
(рис. 9.1, б).
Происходит это за счет возникновения
в контуре ЭДС самоиндукции. Т.к. при
разрядке конденсатора сила тока в цепи
изменяется, то возникающая самоиндукция
стремится поддержать силу тока в цепи
неизменной. В результате, когда конденсатор
полностью разряжен, ЭДС самоиндукции
поддерживает ток в цепи в том же
направлении. Поскольку направление
тока – это условное направление движения
положительных зарядов в цепи, то
конденсатор заряжается так, что знаки
зарядов обкладок противоположны
исходному состоянию (рис.9.1, в).
При этом сила тока в цепи уменьшается,
энергия электрического поля конденсатора
растет. Когда заряд конденсатора
достигает прежнего максимального
значения
![]() ,
то энергия электрического поля снова
достигает максимума
,
то энергия электрического поля снова
достигает максимума
![]() .
.
Определим закон изменения заряда конденсатора во времени. Поскольку энергия контура остается неизменной во времени, то
![]() ,
т.е.
,
т.е.
![]() .
.
Подставим
![]() и
и
![]() :
:
![]() .
.
Учтем,
что
![]() ,
а
,
а
![]() ,
тогда получим
,
тогда получим
![]() ,
,
![]() .
(9.1)
.
(9.1)
Полученное выражение совпадает по форме с дифференциальным уравнением свободных колебаний (соотношение (5.3), п.5.1 первой части):
![]() ,
,
где
- собственная частота колебаний. Поэтому
выражение (9.1) называется дифференциальным
уравнением собственных незатухающих
колебаний
заряда в колебательном контуре. Видно,
что собственная частота колебаний
колебательного контура (обозначим ее
![]() ),
равна
),
равна
![]() .
(9.2)
.
(9.2)
Решением (9.1) является функция зависимости заряда конденсатора от времени:
![]() ,
(9.3)
,
(9.3)
где
![]() – амплитудное значение заряда
конденсатора,
– амплитудное значение заряда
конденсатора,
![]() – начальная фаза колебаний заряда.
– начальная фаза колебаний заряда.
Период собственных колебаний колебательного контура определяется так:
![]() .
(9.4)
.
(9.4)
Соотношение (9.4) называется формулой Томсона в честь получившего его английского физика У. Томсона (лорд Кельвин).
Пользуясь (9.3), выведем закон изменения силы тока в контуре. Для этого найдем производную заряда по времени:
![]()
![]() .
(9.5)
.
(9.5)
Из
сопоставления (9.3) и (9.5) видно, что
колебания силы тока в контуре опережают
колебания заряда по фазе на
![]() ,
а по времени – на четверть периода.
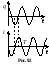
Графики изменения заряда конденсатора
и силы тока в колебательном контуре при
,
а по времени – на четверть периода.
Графики изменения заряда конденсатора
и силы тока в колебательном контуре при
![]() представлены на рис. 9.2.
представлены на рис. 9.2.
Чтобы получить зависимость напряжения на обкладках конденсатора от времени, достаточно воспользоваться определением емкости (3.7):
![]() ,
(9.6)
,
(9.6)
Видно, что напряжение на конденсаторе изменяется со временем синхронно с зарядом конденсатора.
Соотношение
между амплитудным значением напряжения
на конденсаторе и амплитудным значением
силы тока в цепи подобно закону Ома,
поэтому отношение
![]() называется волновым
сопротивлением контура:
называется волновым
сопротивлением контура:
![]() .
(9.7)
.
(9.7)
Проанализируем
изменение энергии, происходящее в
контуре при свободных колебаниях.
Следующие выражения показывают, как
изменяется энергия электрического поля
в конденсаторе и энергия магнитного
поля в соленоиде со временем при нулевой
начальной фазе колебаний:
![]() ,
,
![]() .
.
Поскольку
![]() ,
то
,
то
![]()
![]() (9.8)
(9.8)
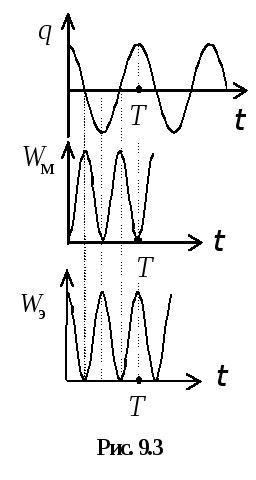
Графики зависимостей энергии магнитного и электрического полей представлены на рис. 9.3.
