Физика 3 семестр / новая папка / Помощь к экзамену / Темы / 34.дивергенция

8.4. Дивергенция и ротор векторного поля

Ранее нами было получено выражение для теоремы Остроградского–Гаусса для электростатического поля в дифференциальной форме (3.23):

, (8.6)

следовательно, дивергенция поля характеризует плотность источников данного поля.

Согласно теореме Остроградского–Гаусса в интегральном виде, . Таким образом, . Следовательно, поток векторного поля через произвольную замкнутую поверхность равен объемному интегралу от дивергенции этого поля по объему, ограниченному поверхностью. В этом и заключается математический смысл теоремы Остроградского, сформулированной им для любого векторного поля.

Если учесть, что , то отсюда будет следовать, что

. (8.7)

Таким образом, мы получили запись третьего и четвертого уравнений Максвелла в дифференциальной форме.

Чтобы записать в дифференциальной форме первое и второе уравнения Максвелла, введем понятие ротора векторного поля. Для произвольного вихревого поля, определяемого в каждой точке вектором , ротором (вихрем) поля называется вектор, равный максимальному пределу отношения циркуляции поля по произвольному замкнутому контуру к площади поверхности, ограниченной контуром, при стремлении последней к нулю (рис. 8.4). При этом ротор направлен в сторону единичной нормали к этой поверхности, согласуясь с направлением вектора по правилу правого винта. Математически это записывается так:

. (8.8)

Поскольку величина предела в (8.8) зависит от ориентации контура, выбираемого в пространстве, то ротор поля по своему физическому смыслу определяет ориентацию векторов в пространстве, степень их “закрученности” по замкнутым линиям (для электрического и магнитного полей ими выступают силовые линии и линии индукции). Вспомним, что для электростатического поля справедливо (1.11) , то . Следовательно, отличие ротора векторного поля от нуля указывает на вихревой характер поля, т.е. на замкнутость его силовых линий.

Рассмотрим второе уравнение Максвелла из системы (8.5):

.

Если подставить это выражение в определение ротора (8.8), то получим

. (8.9)

Выражение (8.9) представляет собой второе уравнение Максвелла в дифференциальной форме. Помножим обе части этого соотношения скалярно на :

.

Теперь проинтегрируем в пределах площадки S:

.

Согласно второму уравнению Максвелла, правая часть полученного выражения равна циркуляции напряженности магнитного поля по контуру, ограничивающему площадку, поэтому

.

Получившееся уравнение справедливо для любого вихревого векторного поля, что было доказано английским математиком и физиком Дж. Г. Стоксом в 1854 г.: циркуляция вихревого поля по произвольному замкнутому контуру равна потоку ротора поля через поверхность, ограниченную контуром (теорема Стокса).

Если теперь рассмотреть первое уравнение из системы (8.5), согласно которому

,

то, согласно теореме Стокса получим, что

. (8.10)

Это и есть запись первого уравнения Максвелла в дифференциальной форме.

В дифференциальной форме записи системы уравнений Максвелла используются понятия дивергенции и ротора векторного поля. Напомним, что, согласно (3.23),

.

Получим теперь выражения для расчета ротора векторного поля .

Поскольку, согласно (8.8), ротор – это вектор, то для его нахождения определим компоненты разложения этого вектора в некоторой системе координат:

. (8.11)

Каждое из этих слагаемых – вектор, направленный по соответствующей координатной оси. Т.к. ротор направлен по нормали к площадке, то это означает, что соответствующие площадки для определения компонент ротора должны быть сориентированы перпендикулярно координатным осям (рис. 8.5). Важно только помнить, что площадки, изображенные на рис. 8.5, проходят через одну точку пространства, в которой и ищется ротор поля (рис. 8.6).

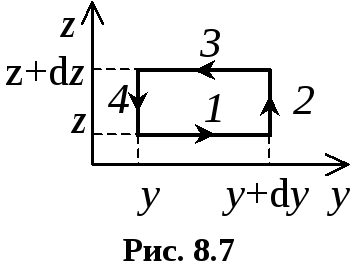
Определим первую компоненту ротора из (8.11). Для этого необходимо рассмотреть ту площадку из трех, изображенных на рис. 8.5, которая перпендикулярна оси Ох. Эта площадка расположена в плоскости zOy (рис. 8.7). Поскольку вектор на этом рисунке смотрит “на нас”, то направление обхода контура, ограничивающего

площадку, должно быть выбрано против часовой стрелки. Тогда циркуляция вектора по выбранному контуру определится так:

,

где каждое из слагаемых представляет циркуляцию вектора по соответствующему элементу контура (они обозначены на рис. 8.7) цифрами. Преобразуем полученное соотношение:

.

Для получения соответствующей компоненты ротора, согласно (8.8), необходимо поделить это выражение на площадь площадки, т.е. на :

.

Аналогично можно получить, что

, .

В окончательном виде запишем

. (8.12)

Оказывается, что это можно короче записать, используя понятие определителя матрицы:

. (8.13)

Итак, соотношения (3.23) и (8.12) или (8.13) позволяют найти дивергенцию и ротор исследуемых векторных полей.

8.5. Система уравнений Максвелла

в дифференциальной форме

Запишем систему уравнений Максвелла (8.5) в дифференциальном виде, объединив (8.10), (8.9), (8.6) и (8.7):

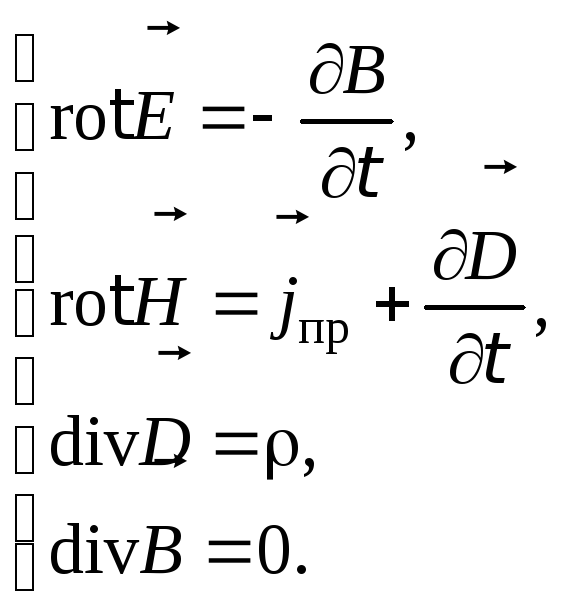
(8.14)

Развернем эти уравнения, использовав полученные соотношения для ротора и дивергенции.

(8.15)

Следует отметить, что уравнения в интегральной форме имеют бóльшую общность, чем в дифференциальной форме, т.к. они остаются справедливыми и тогда, когда в пространстве можно выбрать поверхности, на которых свойства среды или полей меняются скачком. Дифференциальные же уравнения предполагают непрерывность величин, входящих в них. Для использования дифференциальных уравнений дополним их граничными условиями

(8.16)

которые справедливы и для стационарных, и для переменных электрических и магнитных полей.

Системы (8.14) недостаточно для описания полей, даже при наличии заданного распределения зарядов и токов проводимости, т.к. в системе уравнений отсутствуют особенности среды, в которой рассматриваются поля. С этой целью дополним систему еще тремя уравнениями, которые верны для слабых полей и для медленно меняющихся во времени и в пространстве полей:

(8.17)

Итак, рассмотрев систему уравнений Максвелла, мы получили такой вывод: переменное электрическое поле возбуждает вихревое магнитное (2-е уравнение), переменное магнитное возбуждает вихревое электрическое (1-е уравнение), и т.д. Таким образом, если возбудить с помощью колеблющихся зарядов переменное электрическое поле, то в окружающем их пространстве возникают взаимные превращения электрического и магнитного полей. Именно эта совокупность последовательно сменяющих друг друга в пространстве электрического и магнитного полей и называется электромагнитным полем.

Поскольку простейший способ его получения – колебания электрических зарядов, то следующий раздел мы посвятим электромагнитным колебаниям.