9.4. Волновой процесс.

Уравнение плоской волны. Фазовая скорость

Предыдущие разделы данной главы были посвящены теории электрических колебаний. Также в первой части курса мы уже рассмотрели механические колебания. Нами были получены дифференциальные уравнения свободных, затухающих и вынужденных колебаний, а также их решения. Сравнение этих выражений показывает, что характер гармонического колебательного процесса и его причина никак не влияет на вид математического закона, описывающего отклонение колеблющейся величины от положения равновесия. Колебательные процессы в различных системах подчиняются одним и тем же закономерностям. Главное при рассмотрении колебаний – определить, что в какой-либо точке пространства происходит периодическое изменение рассматриваемой физической величины. Если отклонение параметра колебаний начинает передаваться в другие точки пространства, то говорят о возникновении волнового процесса. Следовательно, волна – это физический процесс распространения колебаний, т.е. передачи волнового возмущения из одной точки пространства в другую.

С точки зрения характера колебаний, передаваемых волной, все волновые процессы делятся на два основных класса: поперечные волны и продольные волны. Волна является поперечной, если колебания физической величины, переносимые волной, происходят в плоскости, перпендикулярной направлению движения волны. Примером таких механических волн может быть волна, передающая вдоль шнура его колебания в направлении, перпендикулярном оси шнура.

Волна является продольной, если колебания физической величины, переносимые волной, происходят в плоскости, параллельной направлению движения волны. Пример продольных механических волн – звуковая волна в упругой среде, передающая флуктуации плотности вещества. Упругие колебания частиц вещества в областях повышенной плотности вещества совершаются в направлении движения звуковой волны.

Итак, назовем волновым возмущением S отклонение физической величины от равновесного состояния, передающееся волной в пространстве от одной точки в другую. Длиной волны  называется расстояние, на которое распространятся волновое возмущение за время, равное периоду колебаний Т. Если волновое возмущение распространяется со скоростью , то справедливы следующие соотношения:

; ; . (9.23)

Среди различных точек пространства, до которых дошло волновое возмущение, всегда найдутся такие точки, колебания в которых совпадают по фазе. Геометрическое место точек, колебательный процесс в которых происходит в одной фазе, образует волновую поверхность. По виду этой поверхности волны разделяют на плоские, сферические и т.д. Среди всех волновых поверхностей всегда существует самая внешняя (самая дальняя от источника волны), т.е. волновая поверхность, за которую волновое возмущение еще на распространилось. Эта волновая поверхность называется фронтом волны. Следовательно, волновой процесс можно представить переносом фронта волны во времени и пространстве с некоторой скоростью.

Рассмотрим плоскую волну, переносящую колебания вдоль некоторой оси Ox (рис. 9.11). Фронт такой волны представляет собой плоскость, параллельную плоскости zOy. Пусть фронт движется вдоль оси Ox со скоростью . Допустим, что источник волны располагается в начале координат. Тогда в этой точке совершаются колебания по закону

,

где A – амплитуда колебаний, а  – их частота. В точке, отстоящей от начала координат на расстояние x вдоль оси Ox, колебания начнутся позже, чем в источнике. Задержка во времени составит . Следовательно, закон колебаний в этой точке примет вид

. (9.24)

Видно, что волновое возмущение в различных точках пространства зависит от времени, а в фиксированный момент времени различно в разных точках. Поэтому выражение (9.24) описывает не просто колебания, а волновой процесс. Соотношение (9.24) называется уравнением плоской волны, бегущей вдоль оси Ox. Нетрудно получить, что для волны, бегущей против оси Ox, уравнение имеет вид

.

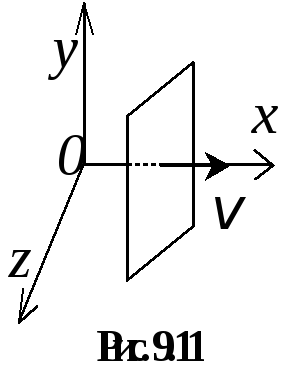
Выражение, служащее аргументом гармонической функции, называется фазой волны. Скорость распространения волнового фронта называется фазовой скоростью волны. Поскольку волновой фронт –совокупность точек с постоянной фазой, то для него . Если фазу продифференцировать по времени, то получим

,

откуда .

Преобразуем (9.24) с учетом (9.23):

, (9.25)

где

(9.26)

называется волновым числом.

Если сравнить соотношения и , то можно сделать вывод, что  – это “пространственный период” волны, а Т – “временной период”. Если частота  показывает число колебаний, которые совершаются за время 2 секунд, то волновое число показывает, сколько длин волн укладывается на длине 2 метров. Между этими параметрами волны существует следующая связь:

. (9.27)

Из соотношения (9.25) видно, что если расстояние между двумя точками пространства равно , то фазы волны в этих точках одинаковы. Поэтому можно дать еще одно определение длины волны: это минимальное расстояние между точками, колебания в которых совершаются в одной фазе. Верно и такое определение: длина волны – это расстояние, на которое смещается волновой фронт за время, равное периоду колебаний.

9.5. Волновое уравнение

Волновым уравнением называется дифференциальное уравнение, решением которого является уравнение волны. Если при анализе какого-либо физического процесса мы получим уравнение, по своей форме соответствующее волновому уравнению, значит исследуемый нами физический процесс имеет волновой характер.

Допустим, исследуется плоская волна, подчиняющаяся уравнению (9.25)

.

Найдем первые и вторые частные производные функции по времени и координате:

; ;

; .

Из полученных соотношений следует, что

.

Если учесть выражение (9.27), то можно получить

. (9.28)

В общем случае, если волна не плоская, а распространяется по всем направлениям прямоугольной системы координат, то уравнение (9.28) записывается в виде

. (9.29)

Полученное соотношение (9.29) называется волновым уравнением. Его принято записывать в сокращенной форме, учитывая, что в левой части уравнения стоит оператор Лапласа (см. п.3.4):

.