7.1. Микротоки. Диамагнитный эффект

Природа появления микротоков связана с незатухающими кольцевыми токами, циркулирующими в частицах вещества. Ампер назвал такие токи микротоками, т.к. эти токи принимают участие в создании магнитного момента вещества (или его части), но не дают вклад в макротоки (токи проводимости, т.е. направленные движения микрочастиц вещества под действием внешних электрических полей).

Рассмотрим модель одноэлектронного атома (рис. 7.1). Такой атом может быть представлен в виде массивной положительно заряженной частицы (ядра), находящейся в центре круговой орбиты электрона, вращающегося вокруг него.

Отрицательно заряженный электрон, вращающийся по орбите, создает орбитальный ток. Направление орбитального тока противоположно направлению вращения электрона. Если скорость вращения электрона по орбите равна , то силу орбитального тока можно найти, разделив величину заряда, проходящего по орбите на время его прохождения:

. (7.1)

Орбитальный ток электрона подобен току, существующему в проводящем витке, а поэтому вращение электрона по орбите создает орбитальный магнитный момент атома, который можно найти, согласно (5.16) так:

. (7.2)

Направление магнитного момента определяется по правилу буравчика и указано на рис. 7.1.

Поместим атом в однородное магнитное поле с индукцией , линии индукции которого перпендикулярны плоскости электронной орбиты (рис.7.2). Это означает, что модуль магнитной индукции возрастает от нуля до , а, следовательно, изменяется магнитный поток через площадь электронной орбиты. Таким образом, согласно закону электромагнитной индукции, внесение атома в поле вызовет появление вихревого электрического поля, силовые линии которого будут замкнуты сами на себя вдоль электронной орбиты. Направление силовых линий определяется по правилу Ленца: вихревое поле должно вызвать ток, препятствующий нарастанию магнитного потока через площадь орбиты.

Напряженность возникающего вихревого электрического поля можно найти из закона электромагнитной индукции (6.7):

,

,

. (7.3)

Со стороны вихревого поля на электрон будет действовать сила . Запишем второй закон Ньютона в виде

,

подставим в него (7.3):

.

Полученное выражение проинтегрируем, учтя изменение скорости электрона от до , а магнитной индукции от 0 до :

,

.

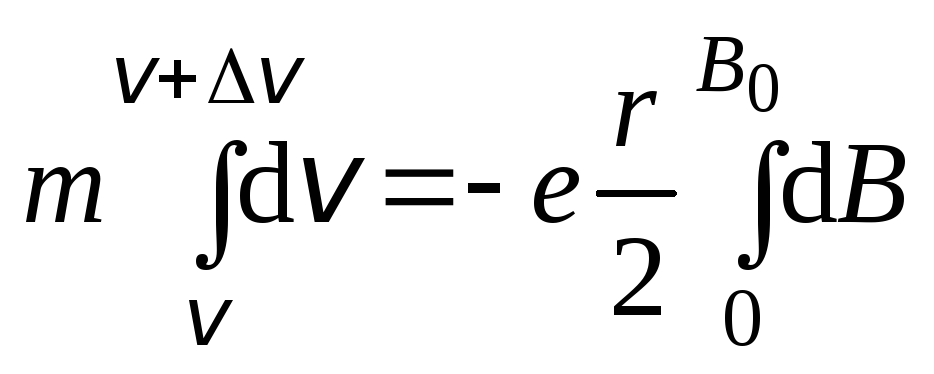Таким образом, скорость электрона изменяется (падает, т.к. вихревое поле вызывает ток, противоположный орбитальному), а, следовательно, изменяется и угловая скорость вращения электрона:

. (7.4)

В соответствии с (7.1), изменению скорости движения электрона будет соответствовать изменение силы орбитального тока:

.

Соответственно, изменится и орбитальный магнитный момент:

. (7.5)

На рис. 7.2 показано, что новый орбитальный магнитный момент атома имеет меньший модуль, чем раньше. Важно, что внесение атома в магнитное поле приводит к тому, что создается магнитный момент такой, что . Этот результат не зависит от направления движения электрона по орбите.

Аналогичный результат можно получить и другим способом. При отсутствии магнитного поля движение электрона по орбите обеспечивается действием на него кулоновского притяжения к ядру:

. (7.6)

При помещении атома в магнитное поле на электрон действует сила со стороны поля. На рис. 7.3 показано, что это воздействие тормозит его движение по орбите. Действительно, второй закон Ньютона для электрона в этом случае запишется так:

.

Решение уравнения дает значение скорости электрона, меньшее, чем из закона (7.6). Магнитный момент атома становится меньше: . Индуцированный магнитный момент направлен против индукции поля: .

Если рассмотреть движение электрона в другую сторону, то воздействие магнитного поля увеличивает скорость электрона (рис. 7.4). Действительно, второй закон Ньютона теперь принимает такой вид:

,

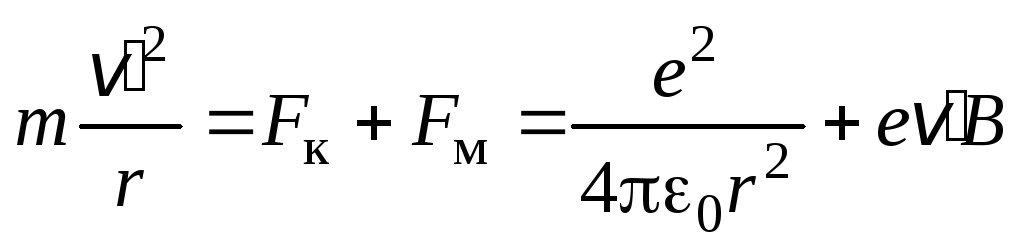а поэтому скорость электрона возрастает. Соответственно, увеличивается и орбитальный магнитный момент: . Однако и в этом случае индуцированный магнитный момент направлен против индукции поля: .

Наконец, необходимо рассмотреть самый общий случай поведения электронной орбиты в магнитном поле (рис. 7.5). Если линии магнитной индукции не перпендикулярны плоскости орбиты, то на электронную орбиту (виток с током) действует вращающий момент (5.34). Под действием магнитного поля, в соответствии с основным уравнением динамики вращения ( – момент импульса электрона), орбита электрона начинает вести себя так, что вектор описывает конус вокруг вектора индукции. Другими словами, возникает прецессия орбиты электрона. Ось орбиты совершает конусообразное движение вокруг линий индукции, а плоскость орбиты электрона периодически изменяет свое положение в пространстве. Частота прецессии, как доказал американский физик Дж. Лармор в 1895 г., составляет (см. 7.4). Формально прецессию можно описать так, что электрон приобретает добавочное движение вокруг вектора по окружности радиуса , т.е. возникает индукционный орбитальный ток. Этот ток вносит добавку в магнитный момент атома:

.

Мы получили результат, аналогичный (7.5). Обобщим сделанные выводы.

При внесении любого вещества в магнитное поле каждая электронная орбита, независимо от направления движения электрона, приобретает индуцированный магнитный момент , направленный против индукции внешнего поля. Этот процесс в физике магнитных явлений называется диамагнитным эффектом. Таким образом, диамагнетизм – свойство, присущее всем веществам, обусловленное действием магнитного поля на электроны в атомах. Единственный результат влияния магнитного поля на орбиту электрона в атоме заключается в прецессии орбиты и магнитного момента атома вокруг оси, проходящей через атом параллельно линиям индукции магнитного поля (теорема Лармора). Другими словами, при внесении атома в магнитное поле, изменяющееся внешнее магнитное поле вызывает явление электромагнитной индукции. Это выражается в том, что вся электронная оболочка приходит во вращательное движение в направлении, при котором индуцируется магнитное поле, препятствующее изменению внешнего магнитного поля.

А если рассмотреть электрон, не вращающийся вокруг ядра в атоме, т.е. свободный? На рис. 7.6. показано, что воздействие на свободно движущийся электрон со стороны магнитного поля (сила ) приводит к его вращению вокруг линий магнитной индукции, что эквивалентно созданию кольцевого тока , магнитная индукция поля которого направлена противоположно внешней. Таким образом, наличие свободных электронов в веществе обязательно уменьшает внешнее поле.

Дальнейшее поведение атома в магнитном поле зависит от ориентации . Если , то атом выталкивается из области более сильного поля (см. п. 5.4), а вещество относится к диамагнетикам. Если , то атом втягивается в область более сильного поля, а вещество относится к парамагнетикам или ферромагнетикам.