1. Определение и вывод уравнения эллипса.

Множ т плоск для люб из котор ∑ расстоян до 2-ух данных т наз фокусами есть вел const и большая чем расстоян между фокусами назыв эллипсом. Пусть F1 и F2 фокусы, расст F1F2=2С C>0, рассмотрем тМ(х,у)->по опред MF1+MF2=2A,(A>0),A>C(*);Выберем сист коорд т чтобы ось ОХ проход через фокусы и были симметр расст относит сист коорд; тF1(C;0) тF2(-C;0); MF½=sqrt(sqr(x±c)+sqr(y-0)); сумма = 2А;….; ;в силу можно предст ;разделим на : ; по опред ур фигуры мы мож утвержд что это элипс. Докажем что т M(x;y) принадлеж элипсу т.е MF1+MF2=2A; MF1=sqrt(sqr(x-c)+sqr(y))>0;из ур элипса выразим sqr(y) и подставим в MF1…..;MF1=a-(c*x1)/a;MF2=-a+(c*x1)/a;сумма =2А;

2. Исследование геометрических свойств эллипса по его уравнению.

Св-ва: 1)эллипс не проходит через (0;0); 2)точки пересечения с осями при у=0 и х=0; 3)симматрия эллипс симметричен относительно обеих осей коорд это св-во позвол исследовать его в 1-ой четв. и затем семитр отоброзить в другие; 4) располож точек эллипса : ;x€(-a;a),y€(-b;b);все точки элипса наход внутр прямоугольн; из ур элипса с учётом четверти : y=;если переменая Х будет ↑ от 0 до А то Y будет ↓ от B до 0; А1А2=2а(больш полуось);В1В2=2b(мал полуось);F1F2=

2c(фок расст);

3. Эксцентриситет и директрисы эллипса. Теорема о директрисах.

Эксцентриситетом эллипса наз вел е=с/а;директрисами 2-е прямые х=±а/е;из опред-> директрисы II малой оси;из нер-ва а>c=>е<1 a/e>a -> эллипс и директр не пересикаются;Т.отношен расстоян от люб М(х;у)эллипса до 1-го из фокусов к расстоян от этойже точки до ближ директр есть велич const;(*);

Док-во: M1F1=a-ex1

M1F2=-a+c*x1/a=-a+ex1

Из рис. M1N1=a/e-x1; M1N2=-a/e+x1; <подставл в *>

4. Определение и вывод уравнения гиперболы.

множ т плоск для люб из кот разн расст до 2-ух данных т наз фокусами есть вел const и меньшая чем раст межд фокусами; F1,F2-фокусы гиперб, F1F2=2c>0; MF1-MF2=±2a,a<c;a>0;выберим сист коорд аналогичн; F1(c;0) F2(-c;0);MF½=sqrt(sqr(x±c)+sqr(y-0));MF1-MF2=±2a;…;a*sqrt(sqr(x+c)+y*y)= ±(a*a+xc)=> (aa-cc)xx+aayy+aa(cc-aa)=0;bb=cc-aa>0; :aabb; ;док-во: M1F1-M1F2=±2a; выразим yy и подставим в M1F1;…;M1F1=±(cx1/a+a);выберим тока MF>0;1)пусть x>0 тогда M1F2= cx1/2+a; из ур гиперб IxI>a; значит найменьшее значен х=а; рассмотрим сх/а -> найменьшее знач дроби : С, но в силу а-с<0; не обходимо взять M1F1 со знаком «-» M1F1=-a+cx/a;2)пусть x<0 аналогичн случаю №1 получ M1F2=-a-cx/a;M1F1=a-cx/a; M1F2-M1F1=-2a

5) Исследование геометрических свойств гиперболы по ее уравнению. Асимптоты гиперболы.

гиперб не прох ч/з (0;0); точки пересичения у=0,х=0;симметрия : т.к в ур гиперб обе коорд наход в кв-ах то гиперб симетр относит оси ОХ и OY это св-во позвол исслед гиперб в одном квадрате; располож т ;IxI>=a;т.е между а и –а нету т гиперб => она не замнкнута; асимптоты y=±bx/a, из этого ур следует что эти прям прох через (0;0) и угловые кооф = ±b/a;

Возмём на гиперб и асимптоте т с одной и тойже абсциссой Х тогда

Ордината Y=bx/a, y=;покажем что Y>y: в первом квадранте x>=a -> xx>xx-aa ->x>sqrt(xx-aa)

Y>y;значит для люб Х гипербола ниже асимптоты;=0; в 1-ой четверти граффики сближ но не пересикаются; y=, X>=a, y↑от т(а;0)до∞; А1,А2 – верш гиперб; А1А2=2а (действит ось гиперб),по тПифаг СС=аа+bb;рассмотр B1(0;b),B2(0;-b),В1В2=2b(мнимая ось)F1F2=2c (фокусы рссстоян)

6) Эксцентриситет и директрисы гиперболы. Равнобочная гипербола.

эксцинтреситетом это е=с/а,с>a => e>1; директрисы : х=±а/е;директриса II мнимой оси, т.к е>1 то a/e<a и директриса будет наход между х=±а;

Т.св-во директрисы:отношен расстоян от люб т гиперб до одного из фокусов к расстоян от этой же точки до соотв директрисы есть велич const; ;;док-во аналогичн случ эллипса;Опр: если b=a то из ур гиперб получ xx-yy=aa; такая гиперб равнобочн; её асимптоты y=±x т.е бисектрис коорд углов;задача: получить ур гиперболы у которой в качестве корд оси выбрана её асимптота такое ур можно получить если повернуть сист координ на угол =-п/4;тогда ось х->X,y->Y ;формулы поворота на люб угол;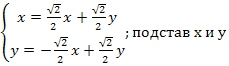в ур гиперб xx-yy=aa;…;k=aa/2;y=k/x-равно бочн гипербола;

7) Вывод уравнения параболы и его исследование.

множ точек плоск для люб из котор расстояние от данной точки наз фокусным = раст до данной прямой наз директрисой;выберим ось ОХ так что бы она проходила через фокус перпендик директрисе аначало координ возмём посередине между фокусом и директрисой; обознач KF=р, тогда F(p/2;0) а директриса им ур x=-p/2; по опред параболы MF=MN

MN=p/2+x;MF=sqrt(sqr(x-p/2)+yy);…;yy=2px;Исследование: проходит через (0;0);т пересикаются с осями корд в (0;0); график симметричен относит ОХ;yy>=0 То при p>0 => x>=0 то для люб т параб располож правее оси OY y=sqrt(2px) – в первом квадранте;

!!!!!8) Полярные координаты точки на плоскости. Связь с декартовыми координатами. Вывод уравнения эллипса, гиперболы и параболы в полярных координатах.

MN=MK+KN=MK+M0N0=rcosγ+M0F1/e=rcosγ+p/e;подставим в MF1/MN=e -> r/(rcosγ+p/e)=e; r=p/(1-ecosγ) – ур эллипса в полярн координ(параболы(эл<1; гип>1;пар=1));для эллипса тМ(-с;р) подставим в ур эллипса xx/aa+yy/bb=1;cc/aa+pp/bb=1;cc=aa-bb;…;p=bb/a – элипс и гипербола;