Вычисление двойных интегралов

Вычисление двойных интегралов сводится к вычислению определенных интегралов.

Теорема 1. Если функция  непрерывна в замкнутой области , ограниченной линиями x = a, y = b (a < b),   и  - непрерывные функции на отрезке [a, b], причем на этом отрезке), то имеет место равенство

 (1)

позволяющее вычисление двойного интеграла свести к последовательному вычислению определенного интеграла от определенного интеграла (или, короче, к вычислению повторного интеграла).

Повторный интеграл, стоящий в правой части равенства (1), обычно записывают в виде:

 

Теорема 2. Если функция  непрерывна в замкнутой области , ограниченной линиями y = c, y = d (c<d),    и   - непрерывные функции на отрезке [c, d], причем всюду на этом отрезке  (рис.3.8.1.) то имеет место равенство

 (2)

позволяющее сводить вычисление двойного интеграла к вычислению повторного интеграла.

Рис. 3.8.1

При вычислении двойного интеграла с помощью повторного по формуле (2) сначала вычисляется внутренний интеграл  при постоянном значении переменной y, в пределах изменения x (для области ) при постоянном значении y,  затем полученная функция от y интегрируется по y в максимальных пределах изменение y для области .

Пример. Вычислить интеграл  по области , ограниченной линиями  Так как выполнены условия теоремы 2, применяя формулу (2), получаем:

.

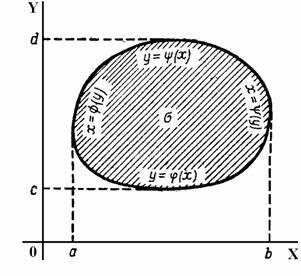
Рис. 3.8.2

 

Если функция непрерывна в замкнутой области , удовлетворяющей одновременно условиям теорем 1 и 2, то при вычислении двойного интеграла 

 можно выбирать любой порядок интегрирования (внешний интеграл брать по x, внутренний – по y или наоборот). Так, например, если граница области каждой прямой, параллельной оси OX, и каждой прямой, параллельной оси OY, пересекается не более чем в двух точках (см. рис. 3.8.2.), то применимы обе формулы (1) и (2), т.е.

Если область  - прямоугольник со сторонами x = a, x = b, y = c и y = d, а f(x, y) – функция, непрерывная в прямоугольнике , то, применяя формулы (1) и (2), получаем:

Например, если  - прямоугольник со сторонами  

В частности, если  то двойной интеграл по этому прямоугольнику оказывается равным произведению двух определенных интегралов.

При вычислении двойного интеграла по области  более сложного вида обычно применяется предварительное разбиение этой области на конечное число частей, удовлетворяющих условиям теорем 1 или 2, интеграл по области  заменяется равной ему суммой интегралов по ее частям, а каждый из полученных интегралов вычисляется по формуле (1) или (2).

Приложения двойн\ого интеграла

Площадь плоской фигуры       Объем цилиндроида      Площадь поверхности:       1. Заданной уравнением z = f(x, y):      2. Заданной параметрически (x = x(u, v), y = y(u, v), z = z(u, v)): где либо      Масса плоской фигуры  ( - плотность).  Статические моменты относительно координатных осей     Координаты центра масс           Моменты инерции       Относительно оси Ох:      Относительно оси Оу:      Относительно начала координат: