Простейшие свойства числовых рядов.

1. Линейность.

Если ряды    и  сходятся (и  их суммы соответственно равны  и ), то линейная комбинация   тоже сходится (к сумме ).

Это свойство вытекает из линейности предела:

 

2. На сходимость ряда не влияет изменение первых членов ряда:

   и  сходятся или расходятся одновременно, если  при   (конечно, суммы, в которые сходятся ряды разные).

Дело в том, что частичные суммы при  этих рядов отличаются на постоянную величину:  (при ). Следовательно, если  имеет предел, то и имеет его (и наоборот).

 

 Знакочередующимся числовым рядом называется ряд

Т. (признак Лейбница): Если для ряда вы-

полняются условия: то этот ряд сходится, причем его суммаи

Рассмотрим частичную суммучлены которой сгруппируем по два:

В силу условия 1) разности в скобках положительны, поэтому последовательностьвозрастающая и

Перегруппируем члены

отсюдаВозрастающая и ограниченная последовательность имеет предел

Для последовательности нечетных суммв силу условия 2) имеем

Таким образом, и ряд сходится

Абсолютная и условная сходимость знакопеременных рядов

Понятие знакопеременного ряда включает в себя как знакочередующиеся ряды, так и ряды с произвольным чередованием знаков своих членов. Знакопеременный ряд  сходится, если сходится ряд . В этом случае знакопеременный ряд  называют абсолютно сходящимся. Сходящийся знакопеременный ряд  называют условно сходящимся, если ряд  расходится. Пример. Исследовать на сходимость знакопеременный ряд   Решение:  . Исследуем на сходимость положительный ряд . Воспользуемся признаком сравнения 1:  . Ряд – сходящаяся бесконечно убывающая геометрическая прогрессия. По признаку сравнения ряд  сходится, поэтому знакопеременный ряд  является абсолютно сходящимся.

 Степенные ряды 

Разложение элементарных функций в степенные ряды

 

Разложение .

Лемма. Если для любого отрезка  при любом , то .

Следствие 1. Легко видеть, . Поэтому  при . Полагая , получаем, что 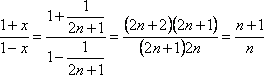 и . Этим разложением можно воспользоваться при вычислении логарифмов и при доказательстве формулы Стирлинга.

Следствие 2. Формула Стирлинга.

Приведем эту формулу без доказательства. .

Применение рядов к приближённым вычислениям

Числовые и функциональные ряды широко применяются в приближённых вычислениях. Рассмотрим это на примерах.   Пример 1. Вычислить  с точностью до 0,001. Воспользуемся разложением  Тогда = 0,0238+0,0046– –0,0008≈0,7475≈0,748. Так как ряд знакочередующийся и 0,0008<0,001, то все слагаемые, начиная с 0,0008, отбрасываем и при этом погрешность не превосходит 0,001.

"Ряды Фурье"

 

Функциональный ряд вида называется тригонометрическим рядом. При этом числа  называются коэффициентами тригонометрического ряда. Тригонометрический ряд также записывают в виде . Коэффициенты, определяемые по формулам , , , называются коэффициентами Фурье функции , а тригонометрический ряд с такими коэффициентами называется рядом Фурье функции . Функция  называется кусочно-монотонной на отрезке , если этот отрезок можно разбить конечным числом точек  на интервалы  так, что на каждом из этих интервалов функция монотонна, то есть либо невозрастающая, либо неубывающая. Теорема. Если периодическая функция  с периодом  является кусочно-монотонной и ограниченной на отрезке , то ряд Фурье, построенный для этой функции, сходится во всех точках. Сумма полученного ряда равна значению функции  в точках непрерывности функции. В точках разрыва функции  сумма ряда равняется среднему арифметическому пределов функции  справа и слева.

 Основные понятия

Комплексным числом z называется выражение вида z=х+iу, где х и у — действительные числа, a i — так называемая мнимая единица, i²=-1.

Если x=0, то число 0+iy=iy называется чисто мнимым; если у=0, то число х+i0=х отождествляется с действительным числом х, а это означает, что множество R всех действительных чисел является подмножеством множества С всех комплексных чисел, т. e. RС.Число х называется действительной частью комплексного числа z и обозначается х=Re z, а у — мнимой частью z, у = Im z.

Два комплексных числа z₁=x₁+iy₁ и z₂=х₂+iy₂ называются равными (z₁=z₂) тогда и только тогда, когда равны их действительные части и равны их мнимые части: х₁=х₂, y₁=у₂. В частности, комплексное число z=х+iy равно нулю тогда и только тогда, когда х=у=0. Понятия «больше» и «меньше» для комплексных чисел не вводятся.

Два комплексных числа z=х+iy и z=х-iy, отличающиеся лишь знаком мнимой части, называются сопряженными.