Модуль 2

Лекція 1

Конгруенції в кільці цілих чисел. Властивості конгруенцій за даним модулем. властивості конгруенцій за різними модулями.

Класи чисел за даним модулем. Повна і зведена система лишків.

Функція Ейлера та її властивості

Означення 1. Числа і називаються конгруентними за модулем , якщо остачі при діленні їх на число рівні між собою, тобто і

Записують це так:

.

Якщо розглядається кілька чисел, конгруентних між собою за тим самим модулем , то роблять такий запис:

наприклад,

Теорема 1. Для того щоб числа і були конгруентні за модулем , необхідно і достатньо, щоб різниця ділилася на , або що теж саме, , де довільне ціле число.

Доведення. Необхідність.

тобто , а позначаючи дістанемо

Достатність.

Отже, число , як і число , при діленні на має остачу, рівну , тобто У зв‘язку з тим, що конгруенції за теоремою 1 тісно пов‘язані з рівностями, вони мають багато властивостей, аналогічних властивостям рівностей.

Властивості конгруенцій при незмінному модулі

Із означення конгруентності випливає розбиття адитивної групи на суміжні класи за підгрупою m і, отже, відношення конгруентності є відношенням еквівалентності і на множині воно рефлексивне, симетричне і транзитивне:

1. Конгруенції за тим самим модулем можна почленно додавати.

Справді,

2. Конгруенції за тим самим модулем можна почленно віднімати.

Справді,

3. До обох частин конгруенції можна додати будь-яке ціле число, тобто з конгруенції випливає , де – довільне ціле число.

Справді, на основі рефлективності конгруентності число с конгруентне з самим собою за будь-яким модулем , у тому числі і за модулем .

Тому, за властивістю 1, маємо:

4. З однієї частини конгруенції можна переносити доданок з протилежним знаком, тобто з випливає

Використовуючи рефлективність конгруентності і властивість 1, дістаємо:

5. До будь-якої частини конгруенції можна додати або відняти довільне ціле число, кратне модулю, тобто з конгруенції випливає або .

Оскільки , то

або

що й треба було довести.

6. Конгруенції за одним модулем можна почленно перемножити.

Справді,

Властивість доведено.

Наслідок. Конгруенцію можна піднести до будь-якого натурального степеня .

Справді, з властивості 6 при умові випливає, що

7. Обидві частини конгруенції можна помножити на те саме ціле число, тобто при і цілому справедлива конгруенція .

Справді, на основі 6 і рефлективності конгруентності маємо:

8. Обидві частини конгруенції можна поділити на їх спільний дільник d, якщо він взаємно простий з модулем m.

Справді, якщо , тобто то

Права частина рівності ділиться на . Тому на ділиться і ліва частина. Оскільки то тобто і Отже, , що й треба було довести.

9. Якщо у виразі

всі коефіцієнти і числа замінити на конгруентні їм за модулем коефіцієнти і числа відповідно, то новий вираз

буде конгруентній за модулем m до заданого

Справді, з конгруентності при всіх випливає . Враховуючи також, що , маємо за властивістю 6

і далі за 1, додаючи всі аналогічні конгруенції, дістанемо

або

що й треба було довести.

Наслідок 1. Якщо то

Наслідок 2. Якщо в многочлені з цілими коефіцієнтами

заданому на множині цілих чисел Z, всі коефіцієнти замінити коефіцієнтами , конгруентними з за модулем , то дістанемо многочлен

конгруентний з многочленом , тобто

Справді,

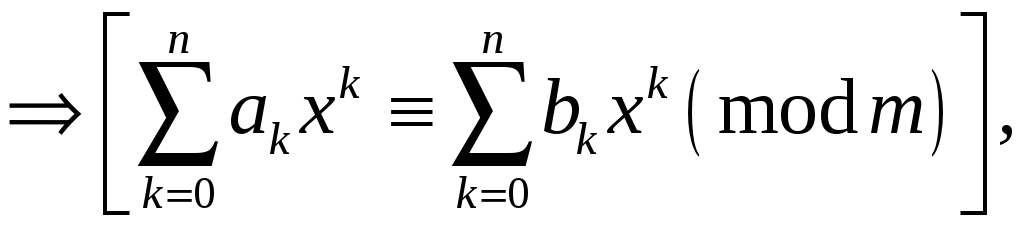тобто

Наслідок 3. Якщо , то для многочлена (1) справедлива конгруенція

Властивості конгруенцій за різними модулями

10. Обидві частини конгруенції і модуль можна множити на те саме ціле число.

Справді,

.

11. Обидві частини конгруенції і модуль можна скоротити на спільний дільник.

Справді,

12. Якщо конгруенція має місце за кількома модулями, то вона має місце і за модулем, який дорівнює спільному найменшому кратному цих модулів.

Припустимо, що

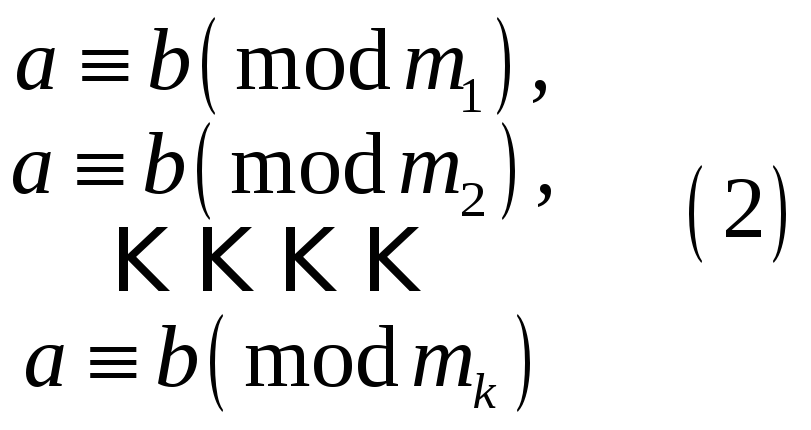
і - найменше спільне кратне чисел . З конгруенцій (2) випливає, що різниця чисел ділиться на числа . Але в цьому випадку, як відомо з властивостей подільності, вона повинна ділитися і на їх найменше спільне кратне . Отже, тобто , що й треба було довести.

13. Якщо конгруенція має місце за модулем , число дільник , то вона має місце і за модулем .

Справді, якщо то

14. Якщо одна частина конгруенції і модуль ділиться на число , то й друга частина конгруенція ділиться на це число.

Справді, з конгруенції випливає рівність

Нехай і . Тоді права частина рівності ділиться на і, отже, . Якщо і , то робимо аналогічний висновок, що .

15. Якщо , то НСД чисел , і , рівні між собою:

Справедливість цього твердження випливає з рівності Справді, ділиться на будь-який спільний дільник чисел і і тому є спільним дільником чисел і . Навпаки, число ділиться на будь-який спільний дільник чисел і , тому є спільним дільником чисел і є ті ж самі, що й чисел і . Зокрема, повинні збігатися і найбільші спільні дільники, тобто

Класи чисел за даним модулем

Відношення конгруентності ділить кільце на класи чисел, конгруентних між собою за даним модулем – класи лишків.

Означення 2. Лишком класу за модулем називається будь-яке число цього класу.

Кільце цілих чисел за модулем розпадається на класів, лишків, кожний з яких породжується будь-яким числом цього класу. До класу лишків, який містить число , належать усі цілі числа виду Цей клас позначають символом , так як число . Іншими словами, справедлива така рівність

( 3 )

при будь-якому цілому значенні t.

Теорема 2. Кожний клас лишків за модулем розпадається на класів лишків за модулем а саме:

.

Доведення. У класі містяться всі числа , конгруентні з за модулем , тобто числа виду Зокрема, він містить таких чисел:

. (4)

За модулем ці числа не конгруентні, так як різниця будь-яких з них не ділиться на , бо є меншою за число . Найбільша з можливих різниць цих чисел – різниця крайніх чисел - менша за . Отже, за модулем числа (4) належать різним класам.

З іншого боку, легко встановити, що будь-яке число з класу конгруентне з одним із чисел (4).

Нехай , тобто . Покажемо тоді, що число і число із (4) конгруентні між собою за модулем .

Це випливає з того, що їх різниця

і тому Отже, .

Отже, клас лишків за модулем m розпадається на такі класи лишків за модулем :

Теорему доведено.

У фактор-множині класів лишків за даним модулем вводяться операції додавання і множення, погоджені з операціями додавання й множення в кільці цілих чисел, а саме:

Означення 3. Сумою класів і називається такий клас , який містить у собі число .

Означення 4. Добутком класів і називається такий клас , який містить у собі число .

Звідси дістаємо:

. (5)

Приклад. За модулем кільце Z цілих чисел утворює фактор-множину класів лишків:

.

Очевидно, .

Теорема 3. Фактор-множина класів лишків за даним модулем є комутативним кільцем з одиницею.

Відповідно до цього фактор-множину класів лишків за модулем m називають фактор-кільцем. Позначають його .

Теорема 4. Якщо - складене число, то є комутативне кільце з дільниками нуля. Якщо ж – просте число, то – поле.

Доведення. Нехай – складене, тобто, наприклад, . Числа і менші за і більші від одиниці. Оскільки і а , то і є дільниками нуля.

Нехай m – просте число. Тоді не існує таких чисел і , щоб добуток їх дорівнював . Тому в кільці не існує й дільників нуля. Покажемо, що в кільці

=

для кожного елемента існує обернений йому , такий, що . У зв‘язку з тим, що – просте число, числа і – взаємно прості, тобто . Але тоді існують такі цілі числа і , що справджується рівність , тобто Але права частина – число і тому . Це означає, що , тобто для елемента з кільця обернений йому елемент . Отже, при m простому є поле. Теорему доведено.

Приклад. Розглянемо кільце Z/7:

Для ненульових елементів знайдемо обернений.