
- •Програма навчальної практики
- •Структура програми навчальної практики з програмування та комп‘ютерної техніки
- •“Автоматизоване управління технологічними процесами”
- •1. Вступ
- •2. Мета і завдання практики
- •3. Зміст практики
- •4. Завдання практики
- •I. Повне дослідження функції
- •III. Створення бази даних засобами Microsoft Access
- •V. Створення презентації звіту до завдань і– IV засобами ms PowerPoint
- •5. Обладнання та програмне забезпечення
- •6. Підведення підсумків практики
- •7. Теоретичні відомості
- •Парність та непарність функції
- •Періодичність та неперіодичність функції
- •Точки перетину графіка функції з осями координат
- •Неперервні та розривні функції, точки розриву
- •Проміжки зростання і спадання функції
- •Екстремуми функції
- •Проміжки опуклості та ввігнутості, точки перегину графіка функції
- •Асимптоти графіка функції
- •4.1 Структури.
- •4.2. Файли даних.
- •Варіанти завдань Завдання і
- •Завдання II
- •Завдання III, IV.
Проміжки опуклості та ввігнутості, точки перегину графіка функції
Графік
функції
![]() на інтервалі
на інтервалі
![]() опуклий, якщо він лежить нижче будь-якої
дотичної, проведеної до графіка функції
на інтервалі
опуклий, якщо він лежить нижче будь-якої
дотичної, проведеної до графіка функції
на інтервалі
![]() .
.
Графік
функції
![]() на інтервалі
на інтервалі
![]() ввігнутий, якщо він лежить вище будь-якої
дотичної, проведеної до графіка функції
на інтервалі
ввігнутий, якщо він лежить вище будь-якої
дотичної, проведеної до графіка функції
на інтервалі
![]() .
.
Точка, яка відокремлює опуклу частину графіка функції від ввігнутої, – точка перегину.
Теорема 1.11. Достатні умови опуклості та ввігнутості графіка функції.
Нехай
існує друга похідна
![]() функції
функції
![]() при будь якому
при будь якому
![]() .
Тоді, якщо
.
Тоді, якщо
![]() ,
то графік функції на інтервалі
,
то графік функції на інтервалі
![]() опуклий. Якщо
опуклий. Якщо
![]() ,
то графік функції на інтервалі
,
то графік функції на інтервалі
![]() ввігнутий.
ввігнутий.
Теорема 1.12. Достатня ознака існування точки перегину графіка функції.
Якщо
у точці
![]() друга похідна функції дорівнює нулю
(
друга похідна функції дорівнює нулю
(![]() )
або не існує і при переході через точку
)
або не існує і при переході через точку
![]() змінює свій знак, то точка
змінює свій знак, то точка
![]() є точкою перегину графіка функції
є точкою перегину графіка функції
![]() .
.
Теорема 1.13. Необхідна умова існування точки перегину графіка функції.
Нехай
функція
![]() має другу похідну для
має другу похідну для
![]() .
Тоді, якщо точка
.
Тоді, якщо точка
![]() є точкою перегину, то друга похідна
функції рівна нулю (
є точкою перегину, то друга похідна
функції рівна нулю (![]() )
або не існує
)
або не існує
Точки,
в яких
![]() або
або
![]() не існує, – критичні точки другого роду.
не існує, – критичні точки другого роду.
Приклад.
Визначити
проміжки зростання і спадання, опуклості
та ввігнутості, точки екстремуму,
критичні точки першого і другого роду,
точки перегину функції
![]() .
.
Область
визначення функції є вся множина дійсних
чисел -
![]() .
.
Перша
похідна функції
![]() :
:
![]() .
.
Визначимо,
при яких
![]() похідна функції рівна нулю:
похідна функції рівна нулю:
![]() ;
;
![]() ;
;
![]() ,
,
![]() .
.
![]() ;
;
![]() .
.
Отже,
точки
![]() та
та
![]() є критичними точками першого роду.
є критичними точками першого роду.
Друга
похідна функції
![]() :
:
![]() .
.
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Розіб‘ємо
критичними точками першого роду
![]() та
та
![]() область визначення функції
область визначення функції
![]() на проміжки та визначимо проміжки
зростання і спадання функції, точки
екстремуму.
на проміжки та визначимо проміжки
зростання і спадання функції, точки
екстремуму.
|
|
|
1 |
|
2 |
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
- |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отже,
функція
![]() зростає при
зростає при
![]()
![]()
![]() і спадає при
і спадає при
![]()
![]() .
Точка
.
Точка
![]()
![]() - точка максимуму, точка
- точка максимуму, точка
![]()
![]() - точка мінімуму.
- точка мінімуму.
Визначимо критичні точки другого роду. Для цього прирівняємо другу похідну функції до нуля.
![]() ,
,
![]() ;
;
![]() .
.
![]() .
.
Отже,
точка
![]() - критична точка другого роду.
- критична точка другого роду.
Розіб‘ємо
критичною точкою другого роду
![]() область визначення функції
область визначення функції
![]() на проміжки та визначимо проміжки
опуклості і ввігнутості функції, точки
перегину.
на проміжки та визначимо проміжки
опуклості і ввігнутості функції, точки
перегину.
|
|
|
1,5 |
|
|
|
- |
0 |
+ |
|
|
|
0,75 |
|
Отже,
функція
![]() опукла при
опукла при
![]()
![]() і ввігнута при
і ввігнута при
![]()
![]() ,
точка
,
точка
![]() - точка перегину.
- точка перегину.
Асимптоти графіка функції
Асимптота – пряма, до якої необмежено наближається поточна точка графіка функції при її віддаленні у нескінченність (під віддаленні у нескінченність розуміємо віддалення у нескінченність відносно початку координат).
Вертикальні асимптоти
Якщо
функція
![]() у точці
у точці
![]() має нескінченний розрив, то пряма
має нескінченний розрив, то пряма
![]() є вертикальною асимптотою графіка
функції. Завжди потрібно визначити
поведінку функції зліва і справа від
асимптоти, тобто визначити односторонні
границі.
є вертикальною асимптотою графіка
функції. Завжди потрібно визначити
поведінку функції зліва і справа від
асимптоти, тобто визначити односторонні
границі.
Похилі асимптоти
Рівняння
похилої асимптоти графіка функції
![]() має вигляд
має вигляд
![]() ,
,
![]() , (1.17)
, (1.17)
![]() . (1.18)
. (1.18)
Якщо хоча б одна з границь (1.17) і (1.18) не існує, то графік похилих асимптот не має.
Зауваження!
При пошуку похилих асимптот доцільно
визначити границі (1.17) та (1.18) при
![]() та при
та при
![]() ,
оскільки у ряді випадків границя зліва
не рівна границі справа.
,
оскільки у ряді випадків границя зліва
не рівна границі справа.
Приклад.
Визначити
асимптоти графіка функції
![]() .
.
Область
визначення функції:
![]() .
.
У точці
![]() функція має нескінченний розрив.
функція має нескінченний розрив.
![]() ;
;
![]() .
.
Отже,
пряма
![]() - вертикальна асимптота.
- вертикальна асимптота.
![]() ;
;
![]()
![]() .
.
Отже,
пряма
![]() - похила асимптота.
- похила асимптота.
Для
дослідження взаємного розміщення
графіків функцій
![]() та
та
![]() розглянемо різницю ординат
розглянемо різницю ординат
![]() та
та
![]() при одному і тому ж
при одному і тому ж
![]() .
.
![]() .
.
При
![]()
![]() ,
тому графік функції
,
тому графік функції
![]() лежить нижче асимптоти.
лежить нижче асимптоти.
При
![]()
![]() ,
тому графік функції
,
тому графік функції
![]() лежить вище асимптоти.
лежить вище асимптоти.
До завдання II
Обчислення матриць
Матриця – математичний об’єкт, що записується у вигляді прямокутної таблиці чисел і припускає такі алгебраїчні операції (додавання, віднімання, множення та ін.) між ними та іншими подібними об’єктами.
Означення
2.1.
Матрицею
розміром
![]() називається прямокутна таблиця чисел,
що містить
називається прямокутна таблиця чисел,
що містить
![]() рядків и
рядків и
![]() стовпців. Числа, які утворюють матрицю,
називають елементами
матриці.
стовпців. Числа, які утворюють матрицю,
називають елементами
матриці.
Матриці прийнято позначати великими буквами, а саму таблицю чисел поміщати у душки
Наприклад:
 ,
,
де
- А
матриця розміром
![]() .
.
Елементи
матриці можуть бути позначені малими
літерами, тоді ця літера позначається
двома індексами. Наприклад , матрицю
розміром
![]() ,
можна записати:
,
можна записати:
 , (2.1)
, (2.1)
![]() -
цей запис показує, що елемент знаходиться
у рядку з номером
-
цей запис показує, що елемент знаходиться
у рядку з номером
![]() і стовпчику з номером
і стовпчику з номером
![]() ,
тобто перший
індекс вказує на номер
рядка,
а другий
- номер
стовпчика.
,
тобто перший
індекс вказує на номер
рядка,
а другий
- номер
стовпчика.
Наприклад в матриці:
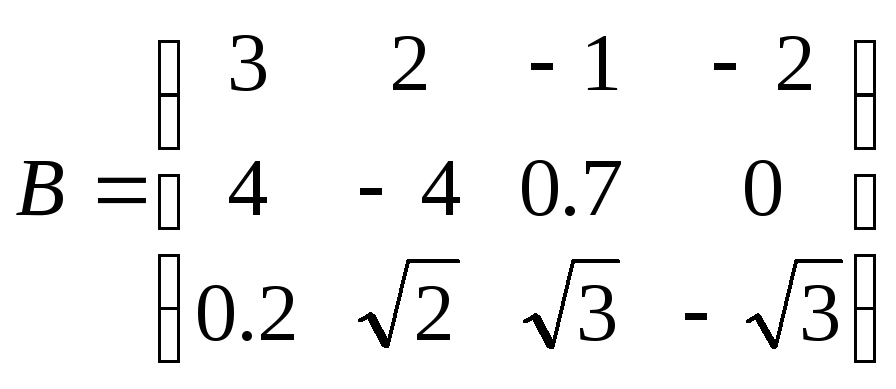 ,
,
де
![]()
![]() .
.
Основні типи матриць:
-
якщо кількість рядків матриці дорівнює кількості стовпчиків, тоді матриця називається квадратною;
-
якщо всі елементи матриці дорівнюють нулю, тоді матриця називається нульовою. Нульова матриця позначається цифрою 0. Як правило, з контексту видно, виявляється цей 0 числом або матрицею;
-
квадратна матриця, у якої всі елементи не головної діагоналі дорівнюють нулю, називається діагональною, (сукупність елементів матриці, які розташовані на відрізку, що з’єднує верхній кут з нижнім, називають головною діагоналлю матриці);
-
квадратна матриця називається верхньою трикутною (нижньою трикутною), якщо всі її елементи, які стоять нижче (вище) головної діагоналі, дорівнюють нулю, (верхня трикутна матриця іноді називається правою трикутною, а нижня трикутна – лівою трикутною);
-
одиничною матрицею називається діагональна матриця, у якої всі елементи головної діагоналі дорівнюють 1, (для позначення одиничної матриці зазвичай використовують літеру Е);
-
дві матриці називаються рівними, якщо вони мають однакові розміри і елементи, що знаходяться на однакових місцях, дорівнюють один одному.
Додавання матриць та множення на число
Додавання визначено тільки для матриць однакових розмірів.
Означення
2.2.
Сумою
матриць
![]() і
і
![]() розмірів
розмірів
![]() ,
є матриця
,
є матриця
![]() такого
ж розміру , у якій
такого
ж розміру , у якій
![]() , (2.2)
, (2.2)
де
![]() ,
,
![]() .
.
Іншими словами, при додаванні матриць, додаються елементи, які знаходяться на однакових місцях.
Наприклад:
 .
.
Означення
2.3.
Добутком
матриці
![]() розміром
розміром
![]() на
число
на
число
![]() називається матриця
називається матриця
![]() такого ж розміру, у якій
такого ж розміру, у якій
![]() , (2.3)
, (2.3)
де
![]() ,
,
![]()
Іншими словами, при множенні матриці на число всі її елементи множаться на це число.
Наприклад:
 .
.
Означення
2.4.
Операцію
віднімання
матриць
можна визначити наступним чином:
![]() , що відповідає відніманню елементів,
які знаходяться на однакових місцях.
, що відповідає відніманню елементів,
які знаходяться на однакових місцях.
Використовуючи операції додавання і множення, можемо знаходити лінійні комбінації матриць, тобто є вирази виду
![]() , (2.4)
, (2.4)
де
![]() -
числа,
-
числа,
![]() - матриці однакових розмірів.
- матриці однакових розмірів.
Наприклад:


Знайдемо
![]() :
:
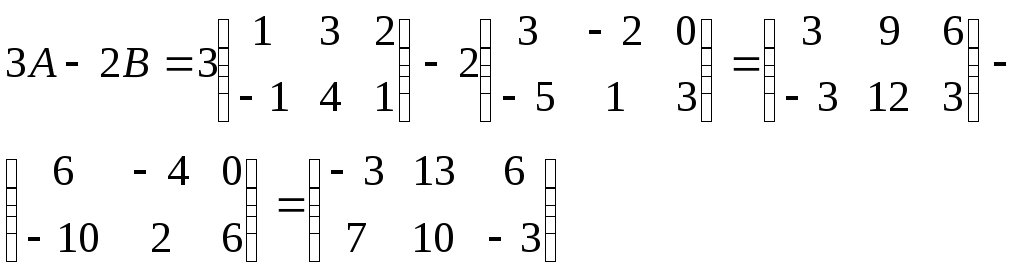
Легко перевірити, що операції додавання матриць і множення матриці на число, які називають лінійними операціями, мають наступні властивості:
-
 -
властивість комутативності;
-
властивість комутативності;
-
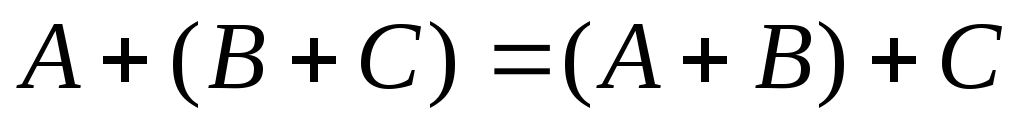 -
властивість асоціативності;
-
властивість асоціативності; -
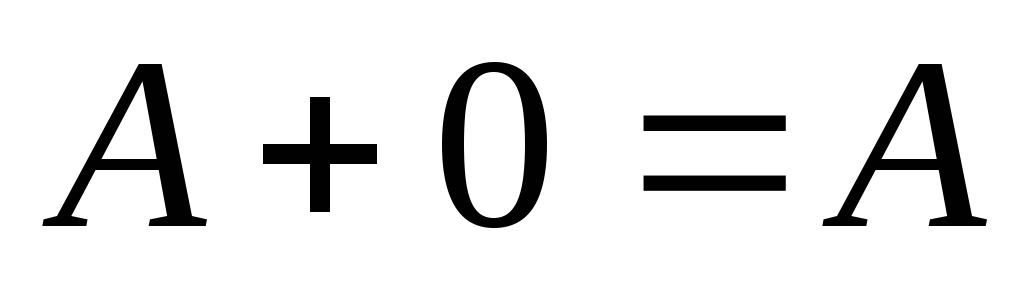 ;
; -
 ;
; -
 -
властивість дистрибутивності;
-
властивість дистрибутивності; -
 ;
; -
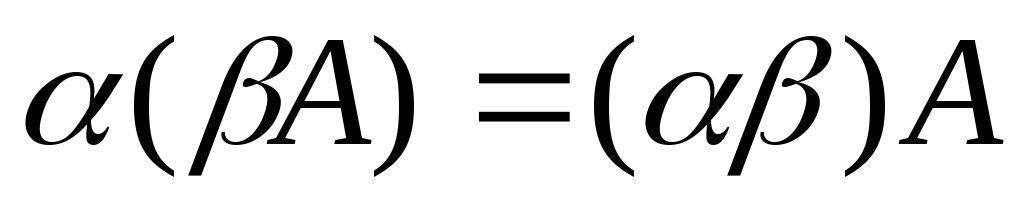 ;
; -
 ;
;
де
![]() - матриці,
- матриці,
![]() -
числа, 0 – нульова матриця.
-
числа, 0 – нульова матриця.
Множення матриць
Означення
2.5
Добуток
матриці
![]() розміром
розміром
![]() на матрицю
на матрицю
![]() розміром
розміром
![]() називається матриця
називається матриця
![]() розмірів
розмірів
![]() ,
елементи якої вираховуються за формулою:
,
елементи якої вираховуються за формулою:
![]() (2.5)
(2.5)
де
![]()
![]() .
.
Насамперед, в цьому виразі потрібно звернути увагу, на важливість порядку множників, потрібно знати, який множник перший, а який - другий.
По-друге, потрібно відмітити, що добуток визначено тільки в тому випадку, якщо кількість стовпців першого множника дорівнює кількості рядків другого. Якщо ця умова не виконується, тоді добуток не визначений.
По-третє, розміри результату множення визначають наступним чином: кількість рядків результату дорівнює кількості рядків першого множника, а кількість стовпців результату дорівнює кількості стовпців другого множника.
Для
того, щоб вирахувати елемент добутку,
який знаходиться в
![]() -ом
рядку і
-ом
рядку і
![]() -ом
стовпчику, потрібно
-ом
стовпчику, потрібно
![]() -ий
рядок першого множника і
-ий
рядок першого множника і
![]() -ий
стовпець другого множника, попарно
помножити їх елементи, що знаходяться
на однакових місцях, і результати додати.
-ий
стовпець другого множника, попарно
помножити їх елементи, що знаходяться
на однакових місцях, і результати додати.
Наприклад,
знайти добуток
![]() і
і
![]() :
:

![]() .
.
Розглянемо
добуток
![]() .
Кількість стовпців у першого множника
.
Кількість стовпців у першого множника
![]() дорівнює
3, кількість рядків у другого множника,
також = 3. Числа співпали, тому, добуток
визначено.
дорівнює
3, кількість рядків у другого множника,
також = 3. Числа співпали, тому, добуток
визначено.
Результатом
множення буде матриця
![]() ,
,
![]() ,
у якій кількість рядків така , яка і у
першого множника, тобто 3, а стовпців
стільки, скільки їх у другого множника,
тобто 2. Тоді матриця
,
у якій кількість рядків така , яка і у
першого множника, тобто 3, а стовпців
стільки, скільки їх у другого множника,
тобто 2. Тоді матриця
![]() буде
мати розміри
буде
мати розміри
![]() .
.
Знаходимо
елемент
![]() .
При його розрахунку використовуємо
перший рядок (1 2 -1) першого множника
.
При його розрахунку використовуємо
перший рядок (1 2 -1) першого множника
![]() і перший стовпець
і перший стовпець
![]() другого
множника
другого
множника
![]() :
:
![]() .
.
Знаходимо
елемент
![]() .
Використовуємо перший рядок (1 2 -1)
першого множника
.
Використовуємо перший рядок (1 2 -1)
першого множника
![]() і
другий стовпець
і
другий стовпець
![]() другого
множника
другого
множника
![]() :
:
![]()
Всі
елементи першого рядка матриці
![]() вирахувані.
вирахувані.
Знайдемо
елемент
![]() .
При його розрахунках приймає участь
другий рядок (3 4 1) першого множника
.
При його розрахунках приймає участь
другий рядок (3 4 1) першого множника
![]() і перший стовпець
і перший стовпець
![]() другого
множника
другого
множника
![]() :
:
![]()
Знайдемо
елемент
![]() .
Використовуємо другий рядок (3 4 0)
першого множника
.
Використовуємо другий рядок (3 4 0)
першого множника
![]() і
другий стовпець
і
другий стовпець
![]() другого
множника
другого
множника
![]() :
:
![]()
Розраховані
всі елементи другого рядка матриці
![]() .
.
Аналогічно знаходимо елементи третього рядка:
![]()
![]()
![]()
Тоді,
 .
.
Розглянемо
добуток
![]() .
Кількість стовпців в першому множнику
.
Кількість стовпців в першому множнику
![]() дорівнює
2, кількість у другому множнику
дорівнює
2, кількість у другому множнику
![]() дорівнює
3. Кількість не співпала, тому, добуток
не визначений.
дорівнює
3. Кількість не співпала, тому, добуток
не визначений.
Відповідь:
 ,
,
де
добуток
![]() не визначений.
не визначений.
Транспонування матриці
Означення
2.6.
Нехай
![]() -
матриця розміром
-
матриця розміром
![]() .
Тоді транспонованою
матрицею
.
Тоді транспонованою
матрицею
![]() називається
така матриця
називається
така матриця
![]() розмірів
розмірів
![]() ,
,
![]() , (2.6)
, (2.6)
де
![]() ,
,
![]()
Транспонована
матриця
![]() позначається
позначається
![]() або
або
![]() .
Операція транспонування заключається
в тому, що рядки і стовпці вихідної
матриці міняються ролями. В транспонованій
матриці перший стовпець служить першим
рядком у вихідній матриці, другим
стовпцем – другий рядок вихідної матриці
і т.п.
.
Операція транспонування заключається
в тому, що рядки і стовпці вихідної
матриці міняються ролями. В транспонованій
матриці перший стовпець служить першим
рядком у вихідній матриці, другим
стовпцем – другий рядок вихідної матриці
і т.п.
Наприклад,
![]() ,
,
 ,
,
![]() ,
,
![]() .
.
Операції, які можуть бути виконані:
-
![]() ,
,
-
![]() ,
,
-
![]() ,
,
де
![]() - число.
- число.
Якщо
добуток
![]() визначено,
тоді
визначено,
тоді
![]()
Нехай
![]() - матриця розмірів
- матриця розмірів
![]() ,
,
![]() - матриця розмірів
- матриця розмірів
![]() .
Тоді
.
Тоді
![]() має
розміри
має
розміри
![]() ,
а
,
а![]() -
розміри
-
розміри
![]() .
Кількість стовпців у
.
Кількість стовпців у
![]() співпадає
з кількістю рядків в
співпадає
з кількістю рядків в
![]() ,
тому добуток
,
тому добуток
![]() на
на
![]() визначено. Розміри цього добутку
визначено. Розміри цього добутку
![]() .
Матриця
.
Матриця
![]() має
розміри
має
розміри
![]() ,
тому
,
тому
![]() -
матриця розмірів
-
матриця розмірів
![]() .
.
-
Обернена матриця
Означення 2.7. Матриця
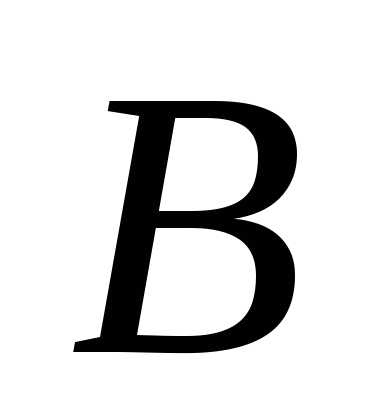 називається
оберненою
матрицею для
квадратної матриці
називається
оберненою
матрицею для
квадратної матриці
 ,
якщо
,
якщо
 .
.З визначення випливає, що обернена матриця
 ,
буде квадратною матрицею того ж порядку,
що і матриця
,
буде квадратною матрицею того ж порядку,
що і матриця
 (інакше одне з добутків
(інакше одне з добутків
 або
або
 буде
не визначено).
буде
не визначено).
Означення
2.8.
Обернена
матриця для матриці
![]() позначається
позначається
![]() .
Таким чином, якщо
.
Таким чином, якщо
![]() існує, тоді
існує, тоді
![]() .
.
Тоді,
з визначення оберненої матриці випливає,
що матриця
![]() є оберненою для матриці
,
тобто
є оберненою для матриці
,
тобто
![]() .
Про матриці
.
Про матриці
![]() і
і
![]() можна говорити, що вони обернені одна
одній або взаємнообернені.
можна говорити, що вони обернені одна
одній або взаємнообернені.
Якщо
матриця
![]() має
обернену, тоді
має
обернену, тоді
![]()
![]() .
.
Так
як визначник добутку матриць дорівнює
добутку визначників, тоді
![]() .
.
![]() ,
тому
,
тому
![]() ,
що не можливо при
,
що не можливо при
![]() .
Із
попередньої рівності випливає
.
Із
попередньої рівності випливає
![]() .
.
Якщо визначник матриці дорівнює нулю, тоді обернена до неї не існує.
Квадратна
матриця
![]() називається особливою,
якщо
називається особливою,
якщо
![]() ,
і не особливою, якщо
,
і не особливою, якщо
![]() .
Якщо обернена матриця існує, тоді вона
єдина.
.
Якщо обернена матриця існує, тоді вона
єдина.
Якщо
квадратна матриця
![]() є не особливою, тоді обернена для неї
існує.
є не особливою, тоді обернена для неї
існує.
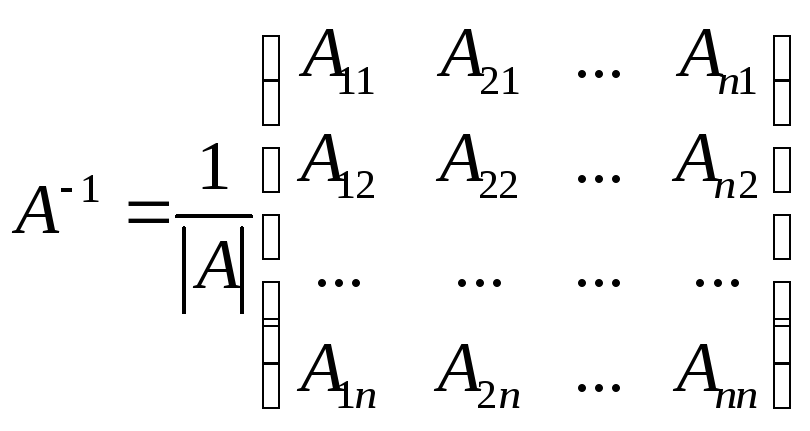 , (2.7)
, (2.7)
де
![]() - алгебраїчні доповнення до елементів
- алгебраїчні доповнення до елементів
![]() .
.
Наприклад, знайдемо обернену матрицю для матриці:

Знайдемо визначник:

.
Так як
![]() ,
тоді матриця
,
тоді матриця
![]() не особлива, і обернена для неї існує.
не особлива, і обернена для неї існує.
Знаходимо алгебраїчні доповнення:









Складаємо обернену матрицю так, щоб перший індекс відповідав стовпцю, а другий – рядку.
 .
.
Найточніше, відповідь треба записати так:

 .
.
Обчисленя матриць в Microsoft Excel
Табличний процесор MS Excel містить великий набір математичних функцій які використовуються для різноманітних обчислень. Розглянемо декілька функцій для роботи з матрицями:
-
МУМНОЖ - добуток матриць;
-
ТРАНСП - транспонування матриці;
-
МОПРЕД - обчислення визначника матриці;
-
МОБР - обчислення оберненої матриці.
Розглянемо функцію множення матриць МУМНОЖ. Ця функція повертає добуток матриць (матриця зберігається в масивах). Результатом є масив з таким же числом рядків, як в масиві 1 і з таким же числом стовпців, як масив 2.
Синтаксис: МУМНОЖ(масив1;масив2), де масив 1, масив 2 – масиви, що перемножуються.
Зауваження:
- кількість стовпців аргументу масиву 1 повинна бути такою ж, як кількість рядків аргументу масиву 2, і обидва масиви повинні містити тільки числа;
- масив 1 і масив 2 можуть бути задані як інтервали, масиви констант або посилання;
- якщо, хоча б одна комірка в аргументах порожня або містить текст, або якщо число стовпців в аргументі масиву 1 відрізняється від числа рядків в аргументі масиву 2, то функція МУМНОЖ повертає значення помилки #ЗНАЧ!.
Приклад: В комірки D9:E10 введена матриця А, а в комірки F9:G10 -матриця В, Потрібно в комірках Н9:І10 отримати результат добутку матриць А·В.
Рішення:
- виділяємо діапазон комірок, де повинен бути отриманий результат добутку -Н9:І10;
- в рядок формул, або користуючись майстром функцій вводимо наступну формулу: =МУМНОЖ(D9:Е10;F9:G10);
- потім натискаємо комбінацію клавіш CTRL+SHIFT+ENTER.
|
Масив 1 |
Масив 2 |
Результат |
||||
|
1 |
2 |
-1 |
3 |
-2 |
1,00 |
1,00 |
|
3 |
4 |
0 |
1 |
0 |
13,00 |
-6,00 |
|
-1 |
2 |
-2 |
4 |
-3 |
-9 |
8 |
До завдання III
Згідно з вимогами виданого варіанту завдання необхідно створити базу даних МS Access, яка повинна: містити інформацію про основні технічні характеристики заданої групи компонентів, забезпечувати зручний інтерфейс введення, редагування, пошуку, сортування, фільтрації та виведення інформації.
Для пошуку технічної інформації в мережі Internet зручно скористатися послугами пошукових серверів і порталів. Адреси деяких з них наведені нижче:
-
google.com.ua
-
aport.ru
-
yandex.ru
-
yahoo.com
-
rambler.ru та ін.
База даних Мicrosoft Access повинна містити чотири основні об’єкти: таблиці, запити, форми (фільтри для форм), звіти.
Перед тим як перейти до створення таблиць, форм і звітів необхідно спроектувати реляційну базу даних, користуючись наступними рекомендаціями:
-
переглянути задачі, які будуть вирішуватися за допомогою бази даних і продумати ті, які можуть виникнути в майбутньому;
-
ідентифікувавши дані і задачі, які необхідно вирішити, розділити їх на групи (наприклад, розділити інформацію про основні характеристики типів пристроїв та інформацію про виробників цих пристроїв). Ці групи в подальшому зручно організовувати як окремі таблиці;
-
визначити типи даних, які будуть зберігатися в кожній таблиці (таблиця виробників, наприклад, може містити їх адреси, номери телефонів, адреси веб-сайтів та ін.);
-
визначити спільні елементи таблиць (тип пристрою може бути спільним елементом таблиці характеристик і таблиці виробників), що необхідно для встановлення зв’язків між таблицями;
-
продумати оформлення форм і звітів;
-
визначити умови вибору для запитів.
Для зручності навігації і роботи з об’єктами бази даних потрібно створити кнопочну форму.
Кнопочна форма – це форма (як об’єкт бази даних), яка містить лише командні кнопки. Командні кнопки використовуються для автоматизації та зручного керування базою даних. Командні кнопки можуть бути створені також і у звіті.
Для програмування командних кнопок (тобто призначення кнопці певних можливостей для керування базою даних) може бути використаний майстер командних кнопок, який пропонує наступні категорії (що містять набір дій) командних кнопок:
1) перехід між записами. Для даної категорії кнопки можна задати наступні дії: перехід до запису, створення нового запису, пошук записів;
2) обробка записів – збереження, відміна останньої дії, проведеної із записом, знищення, друк або створення копії поточного запису;
3) робота з формою – відкривання, закривання, друк, фільтрація, редагування фільтра, поновлення форми;
4) робота із звітом – друк звітів, попередній перегляд звітів перед друком, пересилання звітів у файл, відправлення звітів по електронній пошті;
5) різне – друк таблиць, виконання запитів, виконання макросів, набір номеру телефону.
Для створення командної кнопки, необхідно виконати таку послідовність дій:
1) відкрити форму або запит в режимі конструктора. Якщо створюється кнопочна форма, то необхідно створити пусту форму, вибравши спосіб створення форм Конструктор;
2) відкрити вікно панелі елементів – вибрати пункт меню Вид/Панель элементов;
3) на панелі елементів натиснути клавішу Мастер элементов, а потім клавішу Кнопка. Вказівка маніпулятора перетвориться в хрестик з піктограмою кнопки під ним;
4) встановити хрестик в тому місці форми або звіту, де буде розміщена кнопка та виділити необхідний розмір кнопки. Далі Access завантажить Майстра командних кнопок;
5) вибрати потрібну категорію кнопки із списку;
6) вибрати потрібну дію та натиснути кнопку Далее;
7) ввести надпис або малюнок, які будуть знаходитись на кнопці. Можна використати малюнки, які пропонує Access, або через клавішу Обзор використати файл, що створений графічним редактором;
8) натиснувши кнопку Далее змінити назву (або залишити ту, яку пропонує система) для підпису кнопки. Даною назвою Access однозначно ідентифікує кнопку. Підпис кнопки не відображається на екрані. Натиснути клавішу Готово.
До завдання IV
