13)2-Ыесумматоры с накапливанием суммы, особенности и быстродействие. Схемы и принципы работы сумматора.

Полный одноразрядный двоичный сумматор Одноразрядные двоичные сумматоры строятся по самым различным схемам. Рассмотрим функционирование одноразрядного сумматора, составленного из двух полусумматоров. Полусумматор - это устройство, производящее сложение двух одноразрядных двоичных чисел без учета переноса предыдущего разряда. Составим таблицу истинности полусумматора и полного одноразрядного двоичного сумматора (таблица 1.2)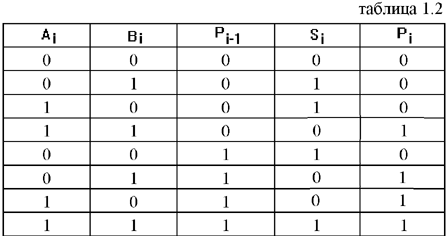Ai, Bi – двоичные цифры i разряда, Pi-1 – перенос из (i-1) разряда, Si – сумма, получившаяся в i разряде, Pi - перенос из i разряда в (i+1) разряд.Первые четыре строчки таблицы 1.2 представляют собой таблицу истинности полусумматора. Сконструируем двоичный полусумматор. Из таблицы истинности следует, что полусумматор должен иметь два входа и два выхода. Следовательно, нам потребуются, по крайней мере, два двухвходовых логических элемента (каждый логический элемент имеет только один выход). Из таблиц истинности логических элементов и полусумматора видно, что для получения суммы двух одноразрядных двоичных чисел необходимо использовать логический элемент исключающее ИЛИ, а для получения переноса – логический элемент 2И. Схема полусумматора, построенного на указанных логических элементах, приведена на рисунке 1.31.

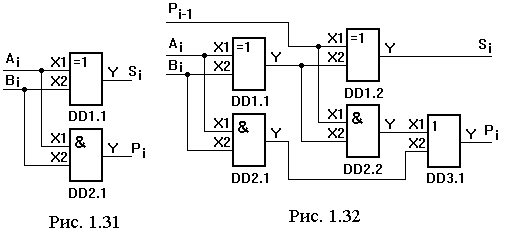
Схема полного одноразрядного сумматора построенного на двух полусумматорах приведена на рисунке 1.32. Один полусумматор используется для сложения i-го разряда двоичных чисел, а второй полусумматор складывает результат первого полусумматора с переносом из (i-1) разряда. Показать самостоятельно, что для получения переноса в полном одноразрядном двоичном сумматоре необходимо сигналы переносов от полусумматоров подать на входы логического элемента 2ИЛИ, на выходе которого получится перенос из полного одноразрядного двоичного сумматора. Рассмотрим следующий пример. Пусть Аi=0, Вi=1, Pi-1=1. В соответствии с таблицами истинности логических элементов 2И и исключающее ИЛИ на выходе элемента DD2.1 будет логический нуль, а на выходе DD1.1 – логическая единица. На входах Х1, Х2 логического элемента DD1.2 сигналы логических единиц, следовательно на выходе этого элемента логический нуль. На выходе элемента DD2.2 сигнал логической единицы. На входе Х1 элемента DD3.1 сигнал логической единицы. Логическая единица на входе логического элемента 2ИЛИ является активным логическим уровнем и, следовательно, на выходе элемента DD3.1 будет сигнал логической единицы. В результате получим сумму в i-ом разряде, равную нулю, а перенос из i-го разряда равный единице. Самостоятельно проанализировать работу полного одноразрядного двоичного сумматора для нескольких других примеров. В главе 2 рассматривается микросхема К155ИМ3, содержащая четырехразрядный двоичный сумматор. Сердцем процессора является арифметико-логическое устройство (АЛУ). АЛУ на микросхеме К155ИП3 изучается с помощью стенда по методике, рассмотренной в главе 2. Накапливающий сумматор обычно представляет собою сочетание комбинацион­ного сумматора и регистра, работающее по формула S - S + А. согласно которой к содержимому сумматора добавляется очередное слагаемое, и результат заме­щает старое значение суммы Структура накапливающего сумматора показана на рис 2 33 Очерёдное прибавление слагзвмого тактируется сиихроимпугьсами СИ Учитывая особенности функционирования, накапливающие сумматоры назы­вают иногда аккумуляторами. В сериях элементов имеются одноразрядные сумматоры, в том числе с до­полнительной входной логикой, двучразрядные и четырехразрядные. При­мером сгандартных ИС сумматоров могут служить микросхемы ИМЗ серии K5S5, содержащие четырехразрядный сумматор с последовательным перено­сом н блок переноса (рис. 2 34), которые непосредственно пригодны для составления из них группового сумматора с ценным переносом.