2.1. Дискретное время. Схема Бернулли, биномиальное распределение

Схемой Бернулли называют последовательность опытов, удовлетворяющую следующим ограничениям:

• каждый опыт имеет конечное число исходов (при 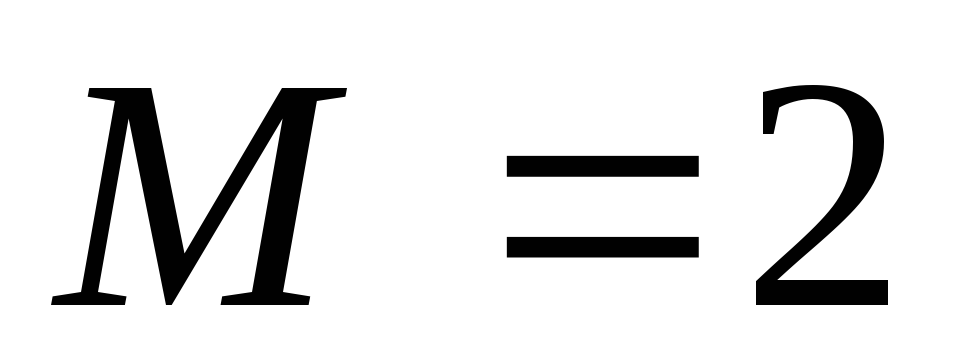имеем двоичную схему Бернулли);

• исходы опытов независимы;

• вероятности исходов не меняются от опыта к опыту (свойство стационарности).

Рассмотрим двоичную схему Бернулли. Один из двух исходов назовем отказом, другой – правильной работой устройства. Найдем распределение вероятностей и числовые характеристики для числа отказов в серии из опытов.

Таблица 2.1. Дискретные распределения вероятностей

Наименование распределения вероятностей	Распределение вероятностей	Числовые характеристики (математическое ожидание , дисперсия )
Бернулли	, ,	,
Геометрическое	, ,	,
Биномиальное	, ,	,
Пуассоновское
Гипергеометрическое
Полиномиальное	;,	;

Обозначим через случайную последовательность исходов опытов, элементы которой выбираются из двоичного множества, причем значение 1 соответствует отказу, а 0 – правильной работе. Заметим, что в силу независимости и стационарности вероятность последовательности равна

.

Обозначим вероятность отказа через , а вероятность правильной работы через . В правой части последнего равенства сомножитель встречается столько раз, сколько было отказов в , остальным позициям соответствует сомножитель . Поэтому

. (2.1)

Здесь мы использовали обозначение для числа ненулевых элементов в последовательности , его еще называют весом Хэмминга последовательности.

Найдем распределение вероятностей для числа отказов в серии из опытов. Очевидно, можно подсчитать как сумму вероятностей всех таких последовательностей , вес которых равен . Из (2.1) ясно, что вероятность последовательности исходов опытов определяется только ее весом (числом отказов), следовательно, все слагаемые в сумме будут одинаковыми. Число различных двоичных последовательностей длины веса равно числу различных выборок по неповторяющихся элементов из совокупности, содержащей элементов (выборки без возвращения, порядок элементов в выборке не существенен). Это число равно числу сочетаний

.

Таким образом,

. (2.2)

Эту формулу называют формулой биномиального распределения.

Вероятность того, что по крайней мере из устройств не исправны подсчитывается по формуле

. (2.3)

Для того, чтобы подсчитать среднее число неисправных устройств, заметим, что

.

Тогда

. (2.4)

Практическое применение формул (2.2) и (2.3) при больших и может вызвать проблемы переполнения разрядной сетки даже при использовании компьютеров с большой разрядностью представления чисел. Проблему можно решить, если в формуле (2.3) при подсчете числа сочетаний вместо умножений выполнять сложение логарифмов. Кроме того, на практике с успехом используются приближенные выражения для биномиального распределения.

С помощью приближения Стирлинга

(2.5)

можно получить приближенные формулы для подсчета числа сочетаний

,

где , и

,

Использованная здесь функция – так называемая функция двоичной энтропии.

Для оценки «хвостов» (малых вероятностей) биномиального распределения можно использовать неравенства

, (2..6)

Для значений близких к используется гауссовское приближение

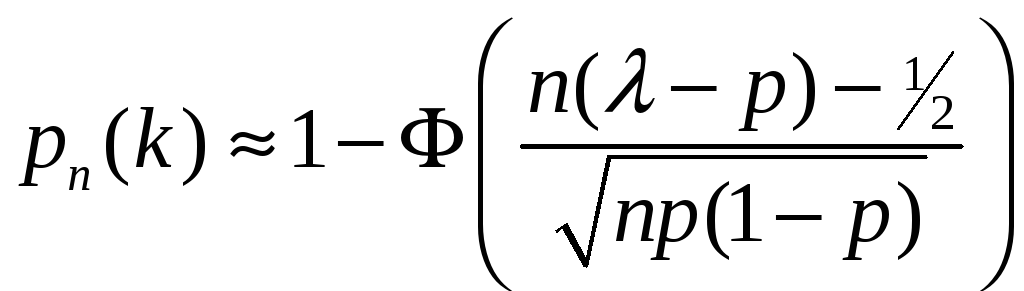, (2.7)

где

– (2.8)

интеграл вероятностей. Приближенные формулы для вычисления интеграла вероятностей приведены в параграфе 2.3.

Использованные в этом параграфе приближения для биномиального распределения заимствованы из [1] и [2].