6.4. Средняя квадратическая погрешность суммы измеренных величин

Рассмотрим функцию, представляющую собой алгебраическую сумму двух величин:

где х и у- — независимые слагаемые.

Случайные погрешности слагаемых и их суммы при однократном из-мерении обозначим соответственно х, у и z, тогда

С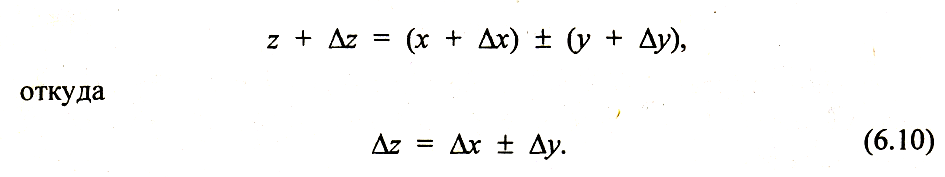ложив левые и правые части п таких уравнений и разделив затем обе части равенства на п, получим:

В соответствии с формулой (6.6) можно написать:

г де [ху] есть сумма произведений случайных погрешностей, которая согласно четвертому свойству случайных погрешностей' стремится к нулю при значительном числе измерений. Тогда, отбросив последнее слагаемое равенства (6.12), окончательно получим:

средние квадратические погрешности функции и аргу-

ментов.

По аналогии для алгебраической суммы п независимых величин

можно записать

Т. е. квадрат средней квадратической погрешности алгебраической сум-мы аргумента равен сумме квадратов средних квадратических погрешно-стей слагаемых.

В частном случае, когда формула (6.15) примет формула (6.15) примет вид:

Если каждое слагаемое было измерено п раз, то, написав п соотноше-ний типа (6.10) и возведя каждое в квадрат, получим п выражений:

5

т. е. средняя квадратическая погрешность алгебраической суммы равно-точных измерений в  п раз больше средней квадратической погрешности одного слагаемого.

Например, если измерено 9 углов 30-секундным теодолитом, то средняя квадратическая погрешность угловых измерений составит

6

6.5. Средняя квадратическая погрешность арифметического среднего

Арифметическое среднее определятся выражением (6.3), которое можно представить как:

где 1/n некоторое постоянное число. Если среднюю квадратическую по-

грешность арифметического среднего обозначить через М, а среднюю квадратическую погрешность одного измерения через т, то согласно (6.15) можно записать:

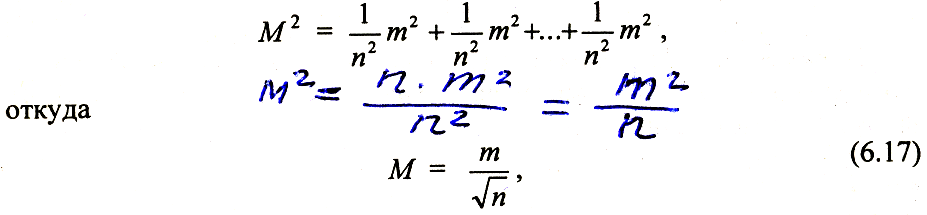
т. е. средняя квадратическая погрешность арифметического среднего в раз меньше средней квадратической погрешности одного измерения. Это свойство средней квадратической погрешности арифметического среднего позволяет повысить точность измерений путем увёличения числа измерений. Например, требуется определить величину угла с точностью ± 15" при наличии 30-секундного теодолита. Очевидно, что если измерить угол 4 раза и определить арифметическое среднее, то его средняя квадратическая погрешность согласно (6.17) составит ± 15".

Средняя квадратическая погрешность арифметического среднего М показывает, в какой мере снижается влияние случайных погрешностей при многократных измерениях.

6.6. Веса результатов неравноточных измерений

При неравноточных измерениях, когда результаты каждого измере-ния нельзя считать одинаково надежными, уже нельзя обойтись опреде-лением простого арифметического среднего. В таких случаях учитывают достоинство (или надежность) каждого результата измерений.

Достоинство результатов измерений выражают некоторым числом, называемым весом этого измерения. Очевидно, что арифметическое среднее будет иметь больший вес по сравнению с единичным измерени-

ем, а измерения, выполненные при использовании более совершенного и точного прибора, будут иметь большую степень доверия, чем те же из-мерения, выполненные прибором менее точным.

Поскольку условия измерений определяют различную величину средней квадратической погрешности, то последнюю и принято прини-мать в качестве основы оценки весовых значений проводимых измере-ний. При этом веса результатов измерений принимают обратно пропорциональными квадратам соответствующих им средних квадратических погрешностей. Так, если обозначить через р и Р веса измерений, имею-щие средние квадратические погрешности соответственно т и М, то можно записать сротношение пропорциональности:

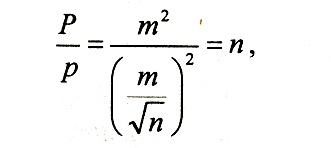Например, если М средняя квадратическая погрешность арифметиче-ского среднего, а т — соответственно, одного измерения, то, как следует из (6.17), можно записать:

т. е. вес арифметического среднего в п раз больше веса единичного изме-рения.

Аналогичным образом можно установить, что вес углового измере-ния, выполненного 15-секундным теодолитом, в четыре раза выше веса углового измерения, выполненного 30-секундным прибором.

При практических вычислениях обычно вес одной какой-либо вели-чины принимают за единицу и при этом условии вычисляют веса осталь-ных измерений. Так, в последнем примере если принять вес результата углового измерения 30-секундным теодолитом за р = 1, то весовое значе-ние результата измерения 15-секундным теодолитом составит Р = 4.