4. Лінійні оператори скінченно-вимірних просторів та їх матриці.

L cкінченно-вимірний лінійний простір , K - поле скалярів.

Оператор A: LL назив лінійним, якщо для будь-якого x, yL, ,K А(x+y)=А(x)+ A(y).

Теорема. L- скінчено вимірний простір dimL=n, Б-базис , Б=(a₁,..., a_n) , b₁,...,b_n- деяка довільна система векторів, тоді існує єдиний лінійний оператор A: LL: А(a₁)= b₁ ,..., А(a_n)= b_n

Доведення: Побудуємо такий оператор : візьмемо x з L , x=₁ a₁ +...+_n a_n. переконаємося, що А(x)=₁ b₁ +...+_n b_n таке відображення лінійне. Візьмемо ,K, тоді x+y=(₁+₁)a₁+...+(_n+_n)a_n, A(x+y)=(₁+₁)b₁+...+(_n+_n)b_n=(₁b₁+...+_nb_n)+(₁b₁+...+_nb_n)=A(x)+A(y)  оператор лінійний. Припустимо, що крім оператора А ми побудували В(a₁) = b₁ ,..., B(a_n)= b_n. Покажемо, що для всякого x з L A(x)=B(x), x=₁ a₁ +...+_n a_n за базисом. Подіємо B(₁ a₁ +...+_n a_n)= ₁B(a₁)+...+ _nB(a_n)= ₁A(a₁)+...+ _nA(a_n)=A(₁ a₁ +...+_n a_n)=A(x).

Візьмемо A: LL, Б=(a₁,..., a_n). Подіємо на вектори базису A, одержимо A(a₁)=₁₁ a₁ +...+_n1 a_n; A(a₂)=₁₂ a₁ +...+_n2 a_n;...; A(a_n)=_1n a₁ +...+_nn a_n.Коефіцієнти запишемо. A - матриця лінійного оператора A у вибраному базисі. За теоремою ця матриця однозначно визначається.

Теорема про обернений оператор: A: LL має обернений оператор  коли його матриця в  базисі невироджена.

Доведення: Припустимо, що А має А^-1,

Якщо , то A^-1 в цьому ж базисі відповідає A^-1.

Навпаки, припустимо, що в деякому Б матриця невироджена: det0, тоді А має А^-1. Розглянемо

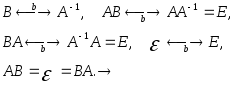
5. Власні вектори та власні числа лінійних операторів .

Розглянемо скінчено вимірний лінійний пр-р L над полем К. А :LL - лін. оп-р, якому відповідає квадратна матриця порядку n з дійсними елементами А=(а_ij); t - незалежна змінна. Тоді матриця А-tЕ, де Е- одинична матриця порядку n, наз. характеристичною матрицею матриці А. Визначник матриці А-tЕ буде многочленом від t степеня n: |А-tE|=A(t) - характеристичний многочлен матриці А, а його корні — характеристичні корні цієї матриці. Подібні матриці мають однакові хар. многочлени. а отже і однакові хар. корені.

Хоча лін. перетворення А може задаватися в різних базисах подібними матрицями , однак всі ці матриці мають один і той же набір хар. коренів.

Характеристичні многочлени двох матр співпадають.

Нехай B=T^-1AT , тоді

B(t)=|B-tE|=|T^-1AT- T^-1(tE)T|=|T^-1(A-tE)T|=|T^-1||A-tE||T|=A(t)

Цей хар. многочлен можна наз. хар. мн-ном самого оп-ра А. Припустимо, що для А  F(основного поля), та вектор b0, bL: А(b)=b. Тоді b - власний вектор оп-ра А, а - власне число. А(b)=b виконується  А(b)-b=  (A-)b=  b Ker(A-), де - одиничний оператор. Це показує, що множина усіх -власних векторів разом з нулем утворюють підпростір пр-ру L. Цей підпростір наз. підпр-ром -власних векторів і познач-ся .

F - власне число оп-ра А  Ker(A-):

Складемо систему лін. рівнянь для обчислення ядра оп-ра (А-):

(a₁₁ -)x₁+ . . . +a_1nx_n=0

 . . .

a_n1x₁+ . . . +(a_nn -)x_n=0

Визначник цієї системи () - хар. многочлен оп-ра А . Отже

1. Число - власне число лін. оп-ра А   є коренем хар. Многочлена цього оп-ра і належить основному полю F . Власних чисел не може бути більше , ніж вимірність поля F.

2. Після того, як знайшли власні числа, можна визначити підпростір -власних векторів. Фіксуємо власні числа  і обчислюємо базисну систему розв’язків цієї системи лін. однорідних рівнянь. Знайдені вектори утворюють базис підпростору .

Алгоритм знаходження власних векторів та власних чисел.

Маємо --вимірний простір над полем і .Зафіксуємо якийсь базис пр. Б і побудуємо в базисі Б. Складемо хар. матр.

. Обчислимо її визначник

.Знайдемо всі корені хар. многочлена, що належать основному полю .Ці корені є власними числами лін. оператора . Для кожного кореня або власного числа складаємо сист. лін. однорідних рівнянь

Знаходимо базисну сист. розв. – це є базис підпр. власних векторів.