Алгебра 2

1.Основні рівняння прямої та площини у просторі. 2

2. Критерій сумісності системи лінійних рівнянь. 3

3.Лінійна залежність та ранг системи векторів, методи обчислення рангів. 4

4. Лінійні оператори скінченно-вимірних просторів та їх матриці. 5

5. Власні вектори та власні числа лінійних операторів . 5

6. Лінійні оператори простої структури. 6

7. Лінійні оператори дійсних евклідових просторів. 8

8. Зведення квадратичних форм до канонічного вигляду. 9

9. Основна теорема про ділимість многочленів. 11

10. Жорданові нормальні форми матриць. 12

Алгебра

1.Основні рівняння прямої та площини у просторі.

А) Загальне рівняння площини у просторі.

Нехай задана площина . Фіксуємо прямокутн. декарт. систему координат. Будь-який ненульовий  вектор наз. нормальним вектором. Площина однозначно визначена нормальним вектором і деякою точкою цієї площини. Нехай n=(a,b,c),. Знайдемо рівняння, що задають цю пл-ну.

Візьмемо довільну Вx,y,z. Розглянемо вектор. Ясно, що (n, АB )=0  . Рівняння площини с зад. норм. вектором: ax+by+cz+(-a+b-c)=0

(-a+b-c)  d

Таким чином, кожна площина у просторі задається таким рівнянням третього порядку і серед коефіцієнтів при невідомих обов‘язково є відмінні від 0.

В) Рівняння площини що проходить через 3 задані точки.

Нехай , , точки пл-ни що не лежать на одній прямій. Візьмемо довільну і введемо вектори



АB=(x1-x0,y1-y0,z1-z0)

AC=(x2-x0,y2-y0,z2-z0)

AD=(x-x0,y-y0,z-z0)

Помітимо, що , – компланарні.Умовою компланарності є рівність 0 мішаного добутку векторів, тобто

x1-x0 y1-y0 z1-z0

x2-x0 y2-y0 z2-z0 = 0

x-x0 y-y0 z-z0

Розкладемо визначник за елементом 1-го порядку

Одерж. рівняння пл.

с) Нормальне рівняння площини у просторі

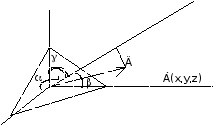
Нехай в прост. задається пл. .З початку корд. На пл. опускається перпендикуляр довжина =р. - одиничний вектор, який перпенд. До пл. і з початку координат напрямлений в бік пл. . Нехай - довільна точка в просторі і нехай точка лежать по різні боки від пл.. . .

а де - кути, які утворює з осями координат. Одержимо - це рівняння наз. нормальним рівнянням пл..

д) Основні рівняння прямої у просторі.

Пряма як перетин площин.

Нехай у просторі задана пряма L, яка є перетином двох паралельних пл. . Фіксуємо дві площини що проходять через цю пряму.

- нормаль вектори 1-ї і 2-ї пл. відповідно, які не колінеарні.Візьмемо довільну точку простору Х з кординатами , тодіколи її координати задов. Систему

Ці рівняння наз. Загальним рівнянням прямої.

Е) Векторне рівняння прямої.

Нехай є пряма L. Довільний ненульовий вектор m(a,b,c) що парал. L наз. спрямовуючим вектором цієї прямої. Зафіксуємо т. . - довільна т. в просторі, зрозуміло, що т. М лежить на прямій L, коли вектор

- колінеарні. Це означає, що існує . Ця рівність наз. Векторним рівнянням прямої L.

Ці рівності наз. Параметричними рівняннями прямої L.

Виразимо параметр t і отримаємо:

- це канонічне рівняння прямої.

2. Критерій сумісності системи лінійних рівнянь.

Розглянемо систему n-лінійних рівнянь з n невідомими.

a11: x1+a12 x2+...+a1n xn=b1

a21: x1+a22 x2+...+a2n xn=b2

.................................................

an1: x1+a22 x2+...+ann xn=bn

Система наз. сумісною, якщо вона має принаймні 1 розв’язок. Сумісна система наз. визначенною, якщо вона має єдиний розв’язок.

Позн. через - визначник, склад. з коєф. при невід. і назвемо головним визначником системи.

a11 a12 ... a1n

= a21 a22 ... a2n

.......................

an1 an2 ... ann

Крім головного- введемо ще n допоміжних визначників. 1-й з них 1, отриман заміною 1 стовб. визн.  на стовбчик вільних членів, 2- 2- зам. 2 ст. і т.д.

a11 a12...a1i-1 b1...a1n

i= a21 a22...a2i-1 b2...a2n

....................................

an1 an2...ani-1 bn... ann

Теорема КРАМЕРА(кільк. рівнянь=кільк. невід)

Якщо гол. визн. квадр. системи лін. рівнянь, відм. від 0, то система, визначена і ії єдиний розв’язок дають формули Крамера:

x1=1/, x2=2/,...xn=n/.