2.5.2. Воздействие струи на преграду
Течение несжимаемой струи на преграде
Давление струи
несжимаемой жидкости на преграду под
углом
будет
.
Радиус пятна струи с количеством движения
при законе распределения давления по
радиусу пятна
будет
.
Это следует из
равенства суммарной реакции преграды
силе тяги струи
.
Реакция
определяется в соответствии с выбранным
законом распределения)
давления
по схеме (рис.2.29).
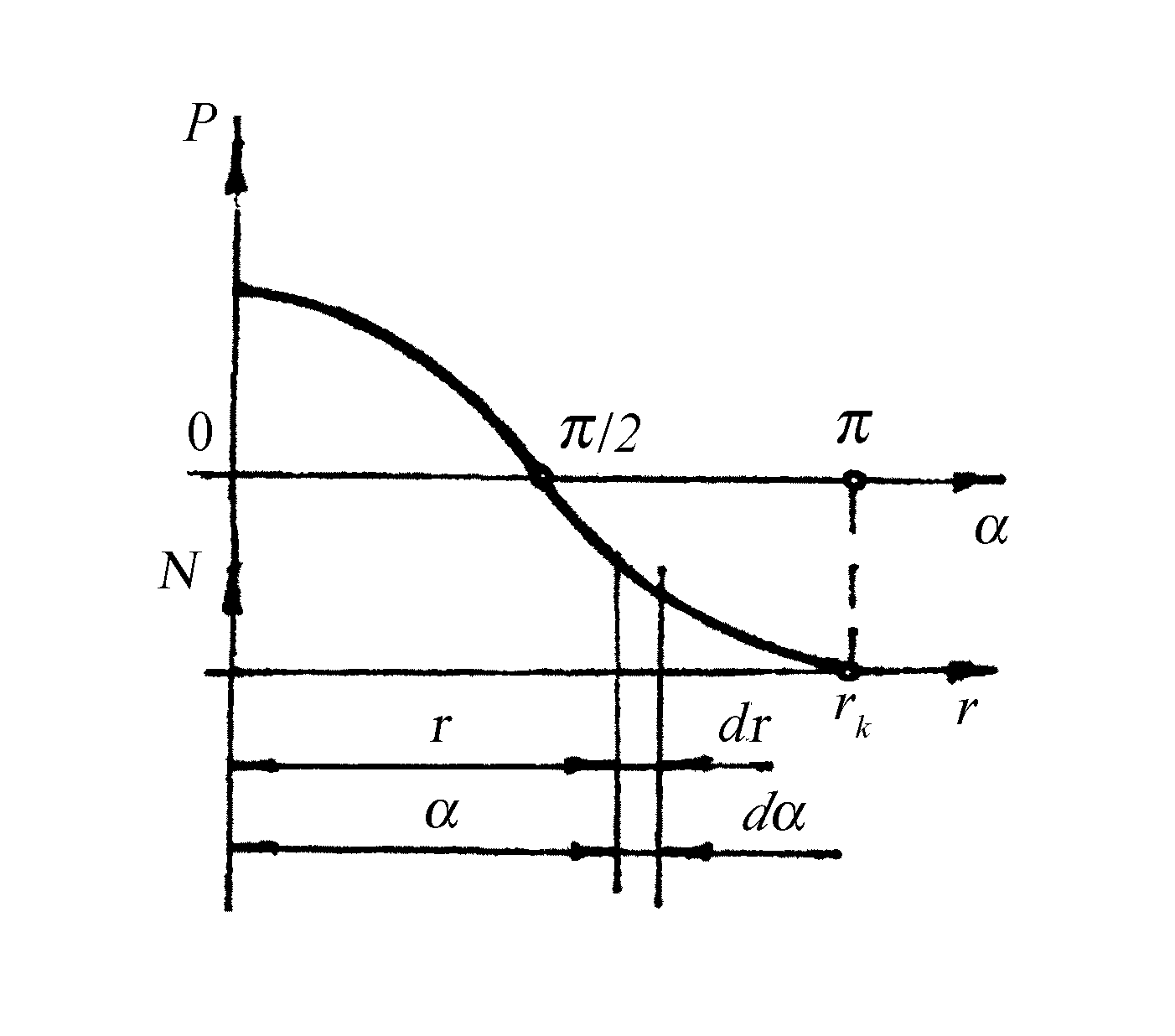
Рис.2.29.
Схема
распределения давления
на преграде
В таком случае получим:
;
;
;
;
;
.
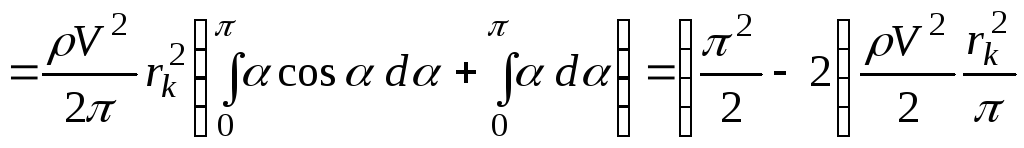Таким образом,
.
Течение сжимаемой струи на преграде
Течение сжимаемой
струи на преграде определяется
закономерностями сверхзвукового
пространственного течения со свободной
границей в среде с
.
Схема течения струи представлена на
рис.2.30.
Для сверхзвуковой
струи линия с давлением
,
будет на радиусе
;
сечение с критическими параметрами
будет на радиусе
.
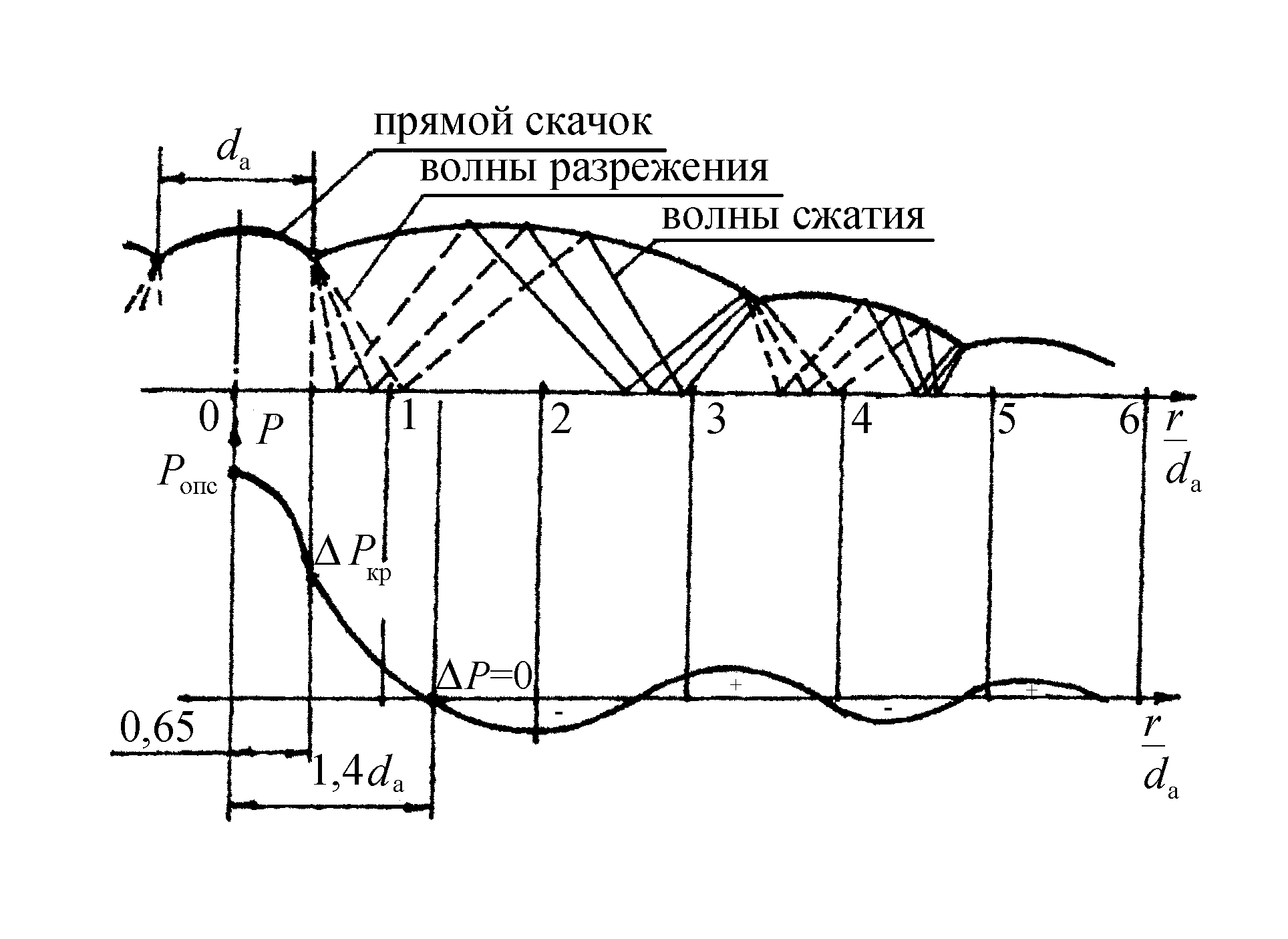
Рис.2.30. Схема течения сжимаемой струи на преграде
В целом давление от сверхзвуковой струи на преграде распределяется сложным образом в силу наличия зон разрежения Прандтль – Майеровского течения и зон уплотнения, аналогично течению струи со свободной поверхностью с синусоидальным распределением амплитуд давления и разрежения с уменьшающимися их максимальными значениями. Можно выделить три кольцевых зоны.
На участке
интеграл давления может в 1,3 раза
превышать
в силу того, что вектор течения на
преграде направлен вверх под углом к
преграде. На основании схемы течения и
экспериментальных данных размер
преграды, на которой реализуется полная
тяга без колебания давления, будет равен
.
Для нерасчетных струй будет иметь место два режима обтекания: с одним максимумом при расположении преграды в узком сечении и двумя максимумами при расположении в широком сечении.
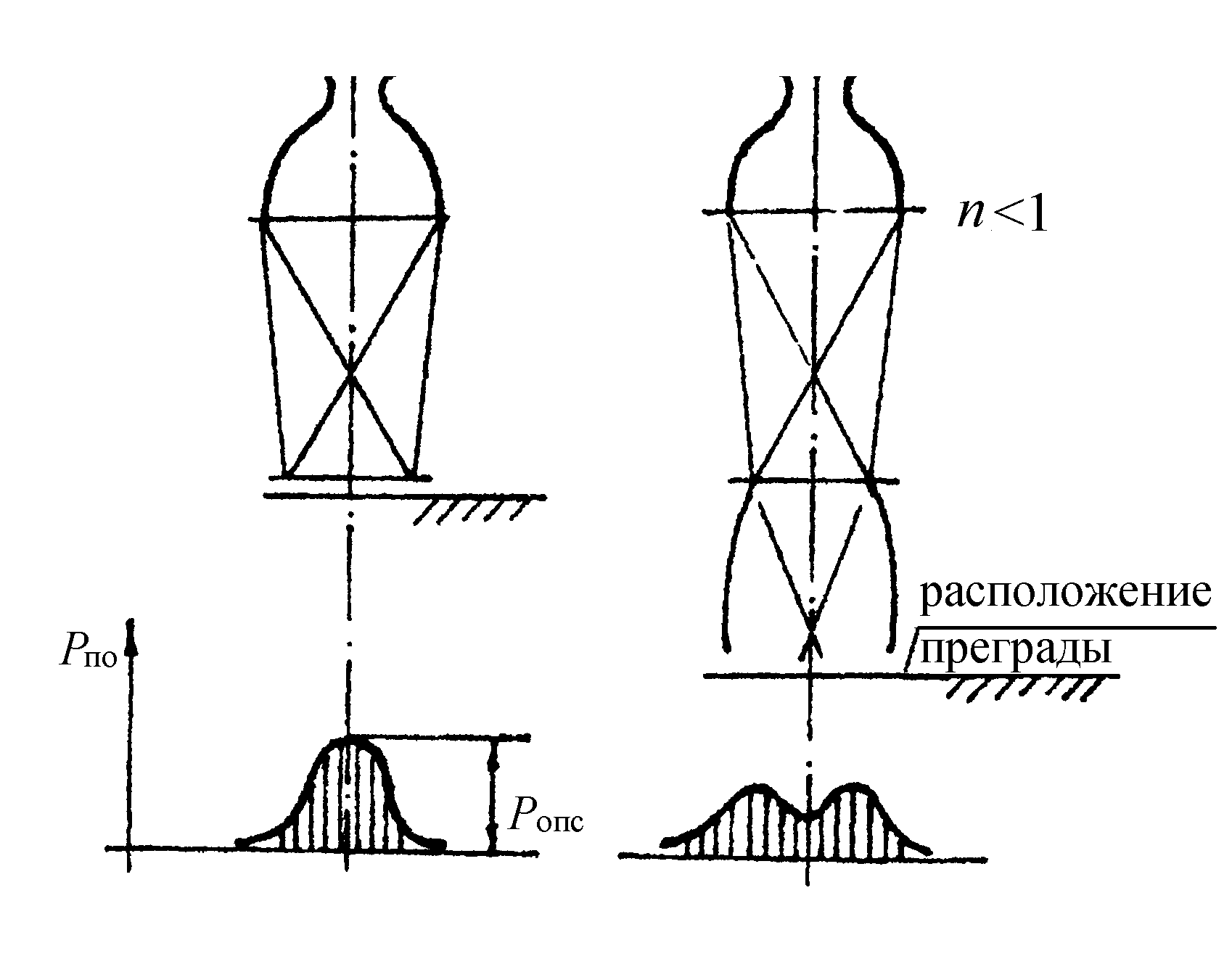
Рис.2.31. Режимы обтекания
Силовое воздействие
на бесконечную преграду при
характеризуется полным поворотом потока
в направлении плоскости под углом
(см. рис.2.23).
При этом 
;
;
;
;
.
Из уравнений расхода и импульса получим
;
.
При
; 
и
;
при
)
.
Давление
определяется из газодинамического
расчета натекающей струи и параметров
на преграде за прямым и косым скачками
согласно разделу 2.2.7.
Силовое воздействие
струи на преграду с ограниченными
размерами (
)
определяется учетом неполноты
поворота струи в направлении
(см. рис.2.32).
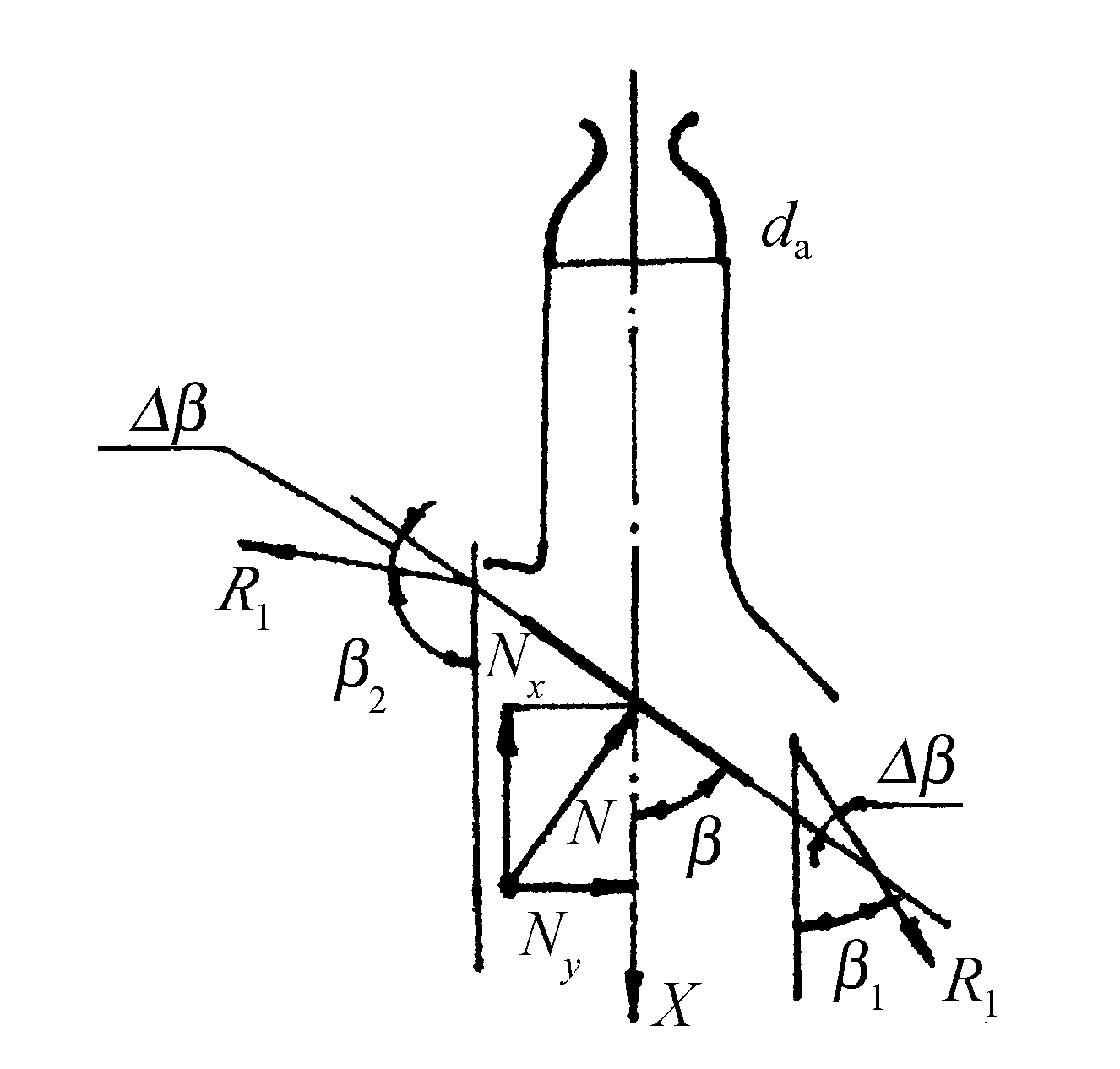
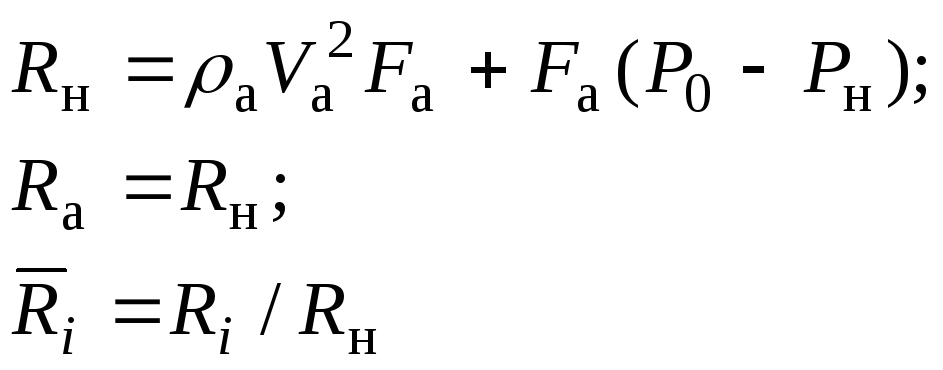
Рис.2.32. Схема натекания струи на плоскость с ограниченными размерами
В данном случае имеем
;
;
;
;
;
;
.
;
при
;
;
при
и
;
при
;
;
при
;
при
;
;
,
тогда для
будет линейная зависимость 
;
при
;
при
.
) Более точное распределение дают эмпирические зависимости.
)
определяется по ударной поляре.