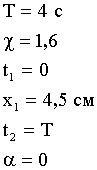- •Содержание:
- •1.1. Физические основы механики
- •1.1.1. Пояснение к рабочей программе
- •1.1.2. Основные формулы
- •1.1.3. Примеры решения задач по механике
- •1.2. Электричество и магнетизм
- •1.2.1. Пояснение к рабочей программе
- •1.2.2. Основные формулы
- •1.2.3. Примеры решения задач по электричеству и магнетизму
- •1.3. Колебания. Волны
- •1.3.1. Пояснение к рабочей программе
- •1.3.2. Основные формулы
- •1.3.3. Примеры решения задач по колебаниям и волнам
- •1.4. Оптика
- •1.4.1. Пояснение к рабочей программе
- •1.4.2. Основные формулы
- •1.4.3. Примеры решения задач по оптике
- •1.5. Статистическая физика и термодинамика.
- •1.5.1. Пояснение к рабочей программе
- •1.5.2. Основные формулы
- •1.5.3. Примеры решения задач по статистической физике и термодинамике
- •1.6. Квантовая физика
- •1.6.1. Пояснение к рабочей программе
- •1.6.2. Основные формулы
- •1.6.3. Примеры решения задач по квантовой физике
1.3.3. Примеры решения задач по колебаниям и волнам
Задача 1. Материальная точка массой 10 г совершает гармоническое колебание с периодом Т=1 с. Определить амплитуду колебаний, максимальную скорость и ускорение колеблющейся точки, если полная энергия точки равна 0,02 Дж.
|
Дано: |
|
|
|
|
|
Найти: |
|
Решение: Уравнение гармонического колебания запишем в виде:
![]() (1)
(1)
где х - смещение материальной точки от положения равновесия; А - амплитуда; ω - циклическая (круговая) частота; t - время; α - начальная фаза.
Скорость колеблющейся точки среды определяется как первая производная от смещения по времени:
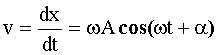
Максимальное
значение скорости:
![]()
Ускорение точки определяется как производная от скорости по времени:
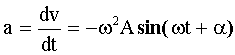
Максимальное
значение ускорения:
![]()
Полная энергия складывается из кинетической и потенциальной энергии и равна максимальной потенциальной или максимальной кинетической энергии:
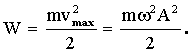
Круговая
частота связана с периодом:
![]() .
Тогда:
.
Тогда:
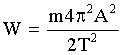
Из этого выражения найдем амплитуду:

Проверим размерность:
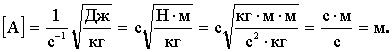
Произведем вычисления:
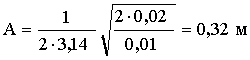
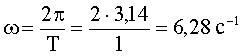
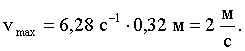
![]()
Ответ: А = 0,32 м, Vmax = 2 м/с, amax = 12,6 м/с2
Задача 2. Найти амплитуду и начальную фазу гармонического колебания, полученного от сложения одинаково направленных гармонических колебаний, данных уравнениями: x1 = 0,02cos (5πt + π/2) м и x2 = 0,03cos (5πt + π/4) м. Построить векторную диаграмму сложения амплитуд.
Дано: x1 = 0,02cos (5πt + π/2)
x2 = 0,03cos (5πt + π/4)
Найти: А, α. Дать векторную диаграмму.
Решение: Построить векторную диаграмму - это значит представить колебание в виде вектора, длина которого равна амплитуде колебаний, а угол наклона к оси абсцисс равен начальной фазе колебаний. При вращении вектора с угловой скоростью ω проекция его конца на ось будет совершать гармонические колебания.
Из условия задачи А1=0,02 м = 2 см, α1= π/2,
А2=0,03 м = 3 см, α2 = π/4.
Векторная диаграмма изображена на рисунке 5.
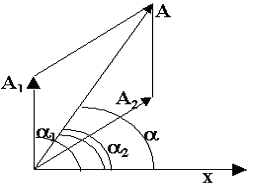 Рис.
5
Рис.
5
Результирующую амплитуду найдем по теореме косинусов:
![]()
Начальная фаза результирующего колебания находится из формулы:
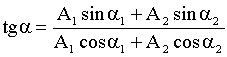
Вычисления:

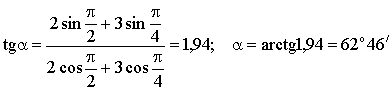
Ответ: А = 4,6 м; α=62о 46′.
Задача 3. Период затухающих колебаний Т = 4 с, логарифмический декремент затухания χ = 1,6; начальная фаза равна нулю. Смещение точки в начальный момент времени равно 4,5 см. Написать уравнение колебаний и найти смещение точки в момент времени спустя период.
|
Дано: |
|
|
|
|
|
Найти: |
|
Решение: Уравнение затухающих колебаний имеет вид:
![]() (1)
(1)
где β - коэффициент затухания, ω - частота затухающих колебаний.
Найдем ω:
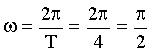
Логарифмический
декремент затухания связан с коэффициентом
затухания:
![]() .
Отсюда:
.
Отсюда:

Подставим ω, β, α в (1) и найдем смещение:
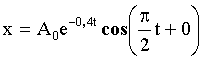
Для начального момента времени при t = 0:

Уравнение колебаний имеет вид:

Смещение
в момент
![]() :
:

|
Ответ: |
|