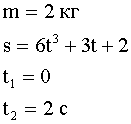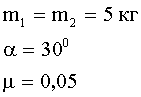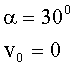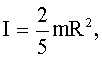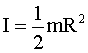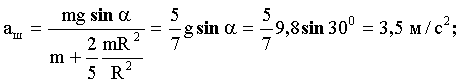1.1.3. Примеры решения задач по механике

Задача 1. Движение тела массой 2 кг задано уравнением: , где путь выражен в метрах, время - в секундах. Найти зависимость ускорения от времени. Вычислить равнодействующую силу, действующую на тело в конце второй секунды, и среднюю силу за этот промежуток времени.

Дано:
Найти:

Решение: Модуль мгновенной скорости находим как производную от пути по времени:

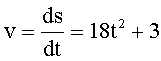
Мгновенное тангенциальное ускорение определяется как производная от модуля скорости по времени:

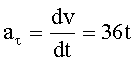
Среднее ускорение определяется выражением:

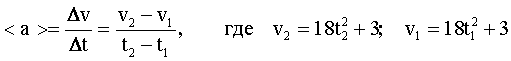
После подстановки:

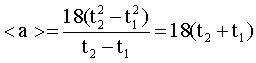
Равнодействующая сила, действующая на тело, определяется по второму закону Ньютона:

Тогда

Ответ:   a(t) = 36t, F = 144 H, = 72 H.

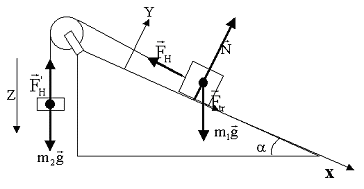
Задача 2. По наклонной плоскости, составляющей с горизонтом угол 30º, движется тело массой 5 кг. К этому телу с помощью нерастяжимой нити, перекинутой через блок, привязано тело такой же массы, движущееся вертикально вниз (рис. 1). Коэффициент скольжения между телом и наклонной плоскостью 0,05. Определить ускорение тел и силу натяжения нити.

Дано:		Рис. 1
Найти:

Решение: Покажем на рисунке силы, действующие на каждое тело. Запишем для каждого из тел уравнение движения (второй закон Ньютона):

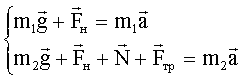
В проекциях на выбранные оси координат:

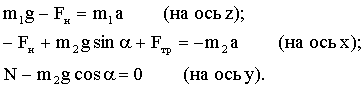
Учитывая, что , где , получим систему уравнений:

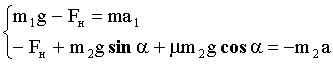
Вычтем из первого уравнения второе:

Искомое ускорение равно:

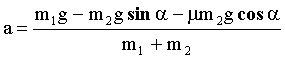
Вычислим ускорение а:

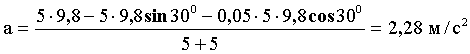
Силу натяжения найдем из первого уравнения системы:

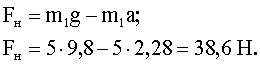
Ответ:    

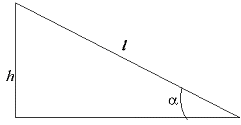
Задача 3. Найти линейные ускорения движения центров тяжести шара и диска, скатывающихся без скольжения с наклонной плоскости. Угол наклона плоскости равен 30º. Начальная скорость тел равна нулю.

Дано:		Рис. 2
Найти:

Решение: При скатывании тела с наклонной плоскости высотой h его потенциальная энергия переходит в кинетическую поступательного и вращательного движения. По закону сохранения энергии:

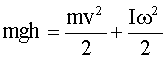                 (1)

где I - момент инерции тела, m - масса.

Длина наклонной плоскости l связана с высотой соотношением (рис. 2):

                 (2)

Линейная скорость связана с угловой:

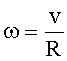                 (3)

После подстановки (2) и (3) в (1), получим:

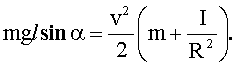                 (4)

Так как движение происходит под действием постоянной силы (силы тяжести), то движение тел - равноускоренное. Поэтому:

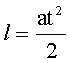                 (5)

и

                 (6)

Решая совместно (4), (5) и (6), получим:

                 (7)

Моменты инерции:

для шара:
для диска:

Подставляя выражение для момента инерции в формулу (7), получим:

для шара:
для диска:

Ответ: