Содержание

1 Введение 5

2 Теория используемых методов и блок-схемы 6

2.1 Метод трапеций. 6

2.2 Блок-схема метода трапеции 7

2.3 Метод прямоугольников. 8

2.3.1 Блок-схема метода левых прямоугольников 9

3 Описание проекта 10

3.1 Основная форма (Form1) 10

3.2 Форма «Решение» (Form2) 12

3.3 Форма «О программе» (Form3) 15

3.4 Форма «Исследование» (Form4) 17

3.5 Форма «График погрешности» (Form5) 19

19

3.6 Модуль. 21

Заключение 22

Список используемой литературы 23

3.7 Литература 23

Приложение A. Код программы 24

1. Введение

В данной курсовой работе, выполненной в Visual Basic, два приблизительных результата, полученных методами прямоугольников и трапеций, сравниваются с точным решением, которое находится расчетом в математическом пакете. Один из методов иллюстрируется (метод прямоугольников), зависимость погрешностей двух данных методов представляется в виде графиков.

Visual Basic (BASIC - Begginners Allpurpose Symbolic Instruction Code, т.е. символический командный универсальный код для начинающего) - один из самых простых языков программирования. Даже при небольшом опыте, программы можно писать, практически не задумываясь. Свою историю этот язык программирования высокого уровня начал в далеком 1963 году. Именно тогда небольшой группой студентов последнего курса Дортмутского колледжа под чутким руководством профессора Дж. Кемени и была разработана самая первая версия этого языка. В то время, помимо Бейсика, широко были распространены также Fortran, Cobol, Algol, PL/1, Focal и Pascal. Из них, до настоящего времени дожили, пожалуй, лишь Паскаль и Бейсик, сильно изменившись при этом. Для построения простого приложения в Visual Basic потребуется всего несколько минут (без учета времени чтения книги). Процесс создания такого приложения заключается в помещении на форму элементов управления, таких как text boxes (текстовые окна), command buttons (командные кнопки или просто кнопки) и т.д. Далее необходимо будет задать свойства для формы и элементов управления, такие как заголовки, цвет, размер и прочие. Наконец, остается написать некоторый код, чтобы приложение имело смысл.

2. Теория используемых методов и блок-схемы

   1. Метод трапеций.

П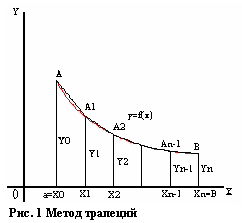усть на отрезке [a, b] задана непрерывная функция y=f(x). Требуется вычислить определённый интеграл . Разделим отрезок [a, b] точками a = x₀, x₁, x₂, ... , x_n-1, x_n = b на n равных частей длины h: . Тогда площадь криволинейной трапеции аАВb будет представлять собой сумму площадей прямолинейных трапеций, ограниченных сверху хордами АА₁, А₁А₂, … , А_n-1B. Так как площадь первой из этих трапеций равна , площадь второй равна и т.д., то

(1)

, или

(2)

Это и есть формула трапеций. Число n выбирается произвольно. Чем больше будет это число и чем меньше, следовательно, будет шаг h, тем с большей точностью сумма, написанная в правой части приближенного равенства (2), будет давать значение интеграла.

2. Блок-схема метода трапеции

h =(b-a)/n

S=0

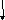
x=a

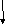
x=x+h

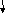
y=f(x)

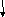
s=s+y

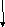
trap=(2*s+f(a)+f(b))/2*h

Блок-схема метода трапеции

3. Метод прямоугольников.

П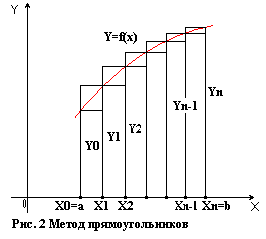усть на отрезке [a, b] задана непрерывная функция y=f(x). Требуется вычислить определённый интеграл . Разделим отрезок [a, b] точками a=x₀, x₁, x₂, ..., x_n=b на n равных частей длины h: .

Обозначим далее через y₀, y₁, y₂, ..., y_n-1, y_n значение функции в точках f(x) x₀, x₁, x₂, ..., x_n, т.е.

y₀=f(x₀), y₁=f(x₁), ..., y_n=f(x_n).

Составим суммы:

y₀h + y₁h + ... + y_n-1h, (3)

y₁h + y₂h + ... + y_nh. (4)

Каждая из этих сумм является интегральной суммой для f(x) на отрезке [a, b] и поэтому приближенно выражает интеграл

(5)

(6)

Это и есть формулы прямоугольников. Из рис. 2 ясно, что если f(x) положительная и возрастающая функция, то формула (1) выражает площадь ступенчатой фигуры, составленной из «левых» прямоугольников, а формула (1’) – площадь ступенчатой фигуры, составленной из «правых» прямоугольников.