Налаштування коефіцієнта затухання виконується зміною елементів, від яких не залежить параметр ω0.

Додаток А

Приклад оформлення титульного аркуша курсової роботи

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ПОЛТАВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

імені ЮРІЯ КОНДРАТЮКА

Факультет інформаційних та телекомунікаційних технологій і систем

Кафедра комп’ютерної інженерії

КУРСОВА РОБОТА

з навчальної дисципліни

„ТЕОРІЯ ЕЛЕКТРИЧНИХ КІЛ”

На тему

Розрахунок arc-фільтра

Виконав студент ________навчальної групи

______________________________________

(прізвище, ім’я, по батькові)

Полтава

2011

Додаток В

Приклад виконання курсової роботи

Завдання на розрахунок arc-фільтра Розрахувати фільтр нч із максимально гладкою характеристикою, яка відповідає наступним вимогам:

1) смуга пропускання: 0 < f < f_п = 3,3 кГц;

2) затухання в смузі пропускання: а < A_{p max} = 1,5 Дб;

3) смуга затримки: 3,8 кГц = f₃ < f < ;

4) мінімально припустиме затухання в смузі затримки: A_{p min} = 38 Дб;

5) коефіцієнт передачі ФНЧ у смузі пропускання |K₀| = 1,0.

6) R_вх = 55 кОм, R_вих = 20 Ом.

Реалізацію ФНЧ виконати ланками на основі операційного підсилювача з інвертуючим входом. Визначити передавальну функцію ФНЧ і побудувати частотну залежність робочого затухання. Забезпечити високу стабільність частотних характеристик фільтра.

Розрахунок фільтра

За формулою ,

де Ω₃ = f_з/f_п=1,25, Е = = 0,64 – рівень нерівномірності,

знаходимо порядок апроксимуючої функції, який дорівнює 20.

За співвідношенням р_k = , k = 1, 2, … m

розраховуємо значення полюсів p_i = λ_i + jω_i апроксимуючої функції.

Оскільки m = 20, то фільтр реалізується десятьма ланками другого порядку.

Визначимо величини параметрів ланок, використовуючи формули

, , ,

де і – номер ланки фільтра, λ_і – дійсна частина, ω_і – уявна частина відповідного кореня.

Результати розрахунків заносимо в таблицю 1.

Таблиця 1

№ ланки	p	ω0	f0, кГц	d	K0
1	-1.02±0.08j	1.022	3.18	1.00	1
2	-0.99±0.24j	1.022	3.18	0.97	1
3	-0.94±0.39j	1.022	3.18	0.92	1
4	-0.87±0.53j	1.022	3.18	0.85	1
5	-0.78±0.66j	1.022	3.18	0.76	1
6	-0.66±0.78j	1.022	3.18	0.65	1
7	-0.53±0.87j	1.022	3.18	0.52	1

Продовження таблиці 1

8	-0.39±0.95j	1.022	3.18	0.38	1
9	-0.24±0.99j	1.022	3.18	0.23	1
10	-0.08±1.02j	1.022	3.18	0.08	1

За формулами для ланки ФНЧ визначаємо співвідношення ємностей конденсаторів та опорів резисторів:

,

(приймаємо |K_0i| = 1).

Виходячи з властивостей операційного підсилювача маємо R₁ << R_вх ОП. Згідно цього приймаємо R₁ = 0,1R_вх ОП, задаємося значенням R₁ = 5,5 кОм і розраховуємо за формулами:

, , , .

Результати обчислень заносимо в таблицю 2.

Таблиця 2

№ ланки	С0min	R0	R0, кОм	R1, кОм	R2, кОм	C1, нФ	C2, нФ
1	2.11	0.48	11.55	5.50	10.50	4.32	9.13
2	2.12	0.50	11.00	5.50	11.00	4.42	9.36
3	2.34	0.50	11.00	5.50	11.00	4.20	9.85
4	2.75	0.50	11.00	5.50	11.00	3.88	10.67
5	3.46	0.50	11.00	5.50	11.00	3.46	11.97
6	4.74	0.50	11.00	5.50	11.00	2.96	14.01
7	7.33	0.50	11.00	5.50	11.00	2.38	17.42
8	13.66	0.50	11.00	5.50	11.00	1.74	23.78
9	36.70	0.50	11.00	5.50	11.00	1.06	38.99
10	324.90	0.50	11.00	5.50	11.00	0.36	116.00

Згідно з таблицею Е-рядів [3] вибираємо номінальні значення ємностей конденсаторів (за допуском не більше 10%).

Результати заносимо в таблицю 3.

Таблиця 3

№ ланки	C1, нФ	C2, нФ	%
1	4.30	9.10	0.15
2	4.30	9.10	0.05
3	4.30	9.10	34.37
4	3.90	11.00	2.46
5	3.60	12.00	24.55
6	3.00	13.00	22.90

Продовження таблиці 3

7	2.40	16.00	18.47
8	1.60	24.00	8.95
9	1.10	39.00	5.76
10	0.36	120.00	2.53

З урахуванням прийнятих ємностей перерахуємо величини резисторів за формулами: ,, .

З результатів аналізу таблиці 3 робимо висновок що для ланок №3, 5, 6, 7 С⁰ відрізняється від С⁰_min більш ніж на 10%, що не вкладається у допуск на номінали застосованих деталей, тому для зміни коефіцієнта підсилення (затухання) потрібно змінити R₂ так як . Для цього визначаємо потрібне значення , а потім і .

Результати розрахунків заносимо у таблицю 4.

Таблиця 4

№ ланки	R0, кОм	R1, кОм	R2, кОм	K0
1	11.60	5.52	10.51	1.00
2	11.32	5.66	11.31	1.00
3	8.71	4.36	4.50	1.94
4	10.81	5.40	10.29	1.00
5	9.18	4.59	5.72	1.61
6	9.51	4.76	6.12	1.56
7	9.84	4.92	6.88	1.43
8	11.42	5.71	9.58	1.19
9	10.31	5.16	9.20	1.12
10	10.77	5.39	10.24	1.00

Згідно таблиці Е-рядів визначаємо номінальні значення опорів резисторів і занесемо їх в таблицю 5.

Таблиця 5

№ ланки	R0, кОм	R1, кОм	R2, кОм
1	12.00	5.60	11.00
2	11.00	5.60	11.00
3	91.00	4.30	4.30
4	11.00	5.60	10.00
5	91.00	4.70	5.60
6	91.00	4.70	6.20
7	91.00	4.70	6.80
8	11.00	5.60	9.10
9	10.00	5.10	9.10
10	11.00	5.60	10.00

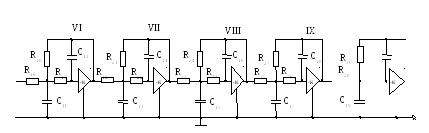
Після розрахунку номіналів елементів фільтра зображуємо принципову схему фільтра (додаток №1) і специфікацію до неї (додаток №2).

Для побудови графіку робочого загасання необхідно:

1. З урахуванням визначених номіналів конденсаторів та резисторів розрахувати для кожної ланки наступні параметри:

,

.

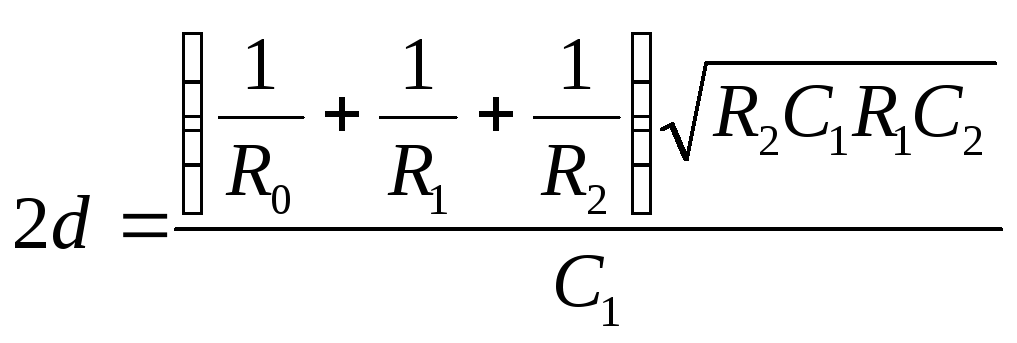Результати розрахунків занести в таблицю 6.

Таблиця 6

№ ланки	2d	ω0
1
2
3
4
5
6
7
8
9
10

2. Для кожної ланки з урахуванням виразу передавальної функції ланки ФНЧ

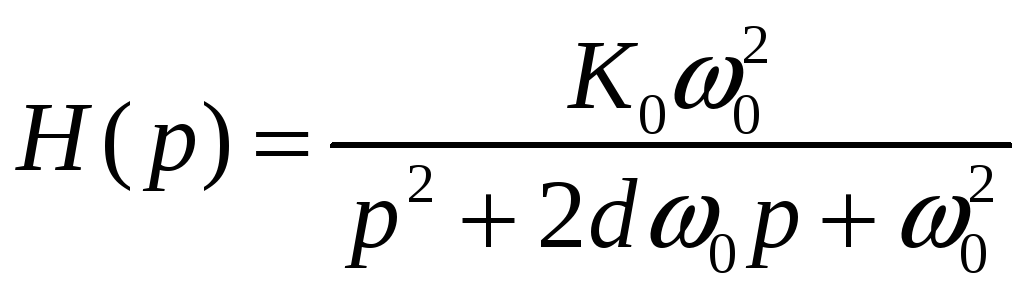
з урахуванням параметрів, представлених в таблиці 6, визначить передавальні функції кожної ланки.

Результати занести в таблицю 7.

Таблиця 7

№ ланки	Hi(p)
1
2
3
4
5
6
7
8

Продовження таблиці 7

9
10

3. На основі отриманих передавальних функцій, замінивши оператор р на оператор j2πf, отримати комплексну передавальну функцію кожної ланки.

Результати занести в таблицю 8.

Таблиця 8

№ ланки	Hi(j2πf)
1
2
3
4
5
6
7
8
9
10

4. На основі отриманих комплексних передавальних функцій кожної ланки виразить комплексну передавальну функцію усього фільтра

.

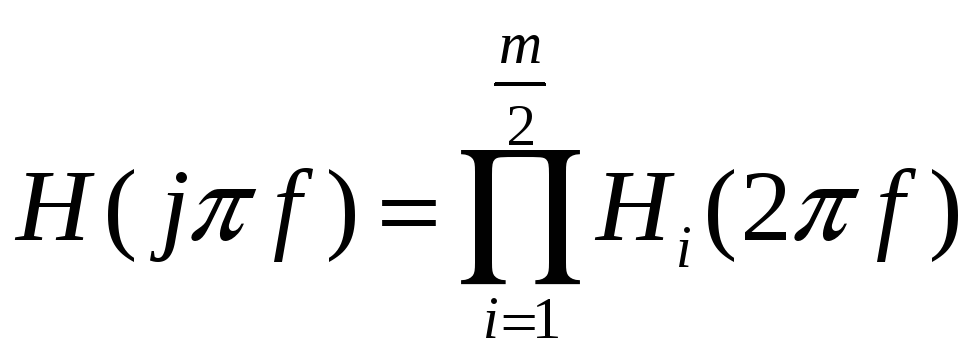5. Використовуючи комплексну передаточну функцію фільтра визначить характеристичне робоче загасання фільтра

6. Будуємо графік характеристичного робочого загасання.

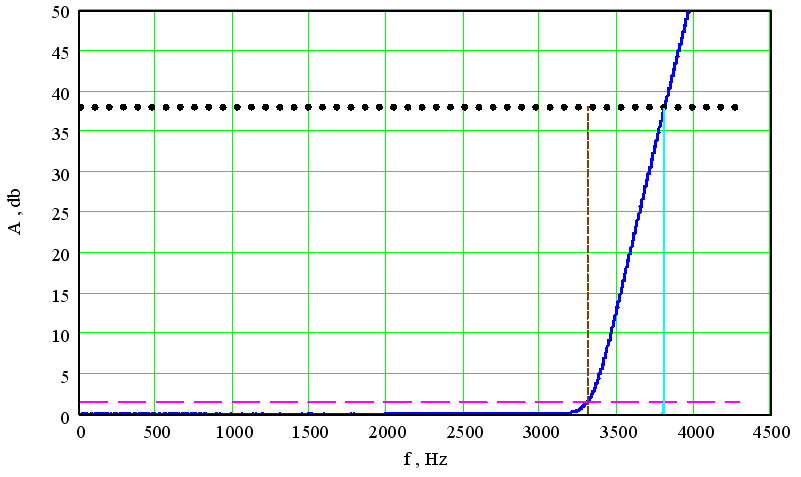Рисунок 1

Додаток 1

V

R₁₄

R₁₅

C₉

C₁₀

R₂₉

C₂₀

Χ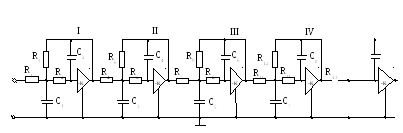

Додаток 2

Специфікація елементної бази фільтра

Nп/п	Позначення на схемі	Найменування	Кількість
1.	R1 R2 R3 R4 R5 R6	Резистори ГОСТ 2825-67 МЛТ - 0,125 -11к ± 5% МЛТ - 0,125 -5,6к ± 5% МЛТ - 0,125 -12к ± 5% МЛТ - 0,125 -11к ± 5% МЛТ - 0,125 -5,6к ± 5% МЛТ - 0,125 -11к ± 5%	1 1 1 1 1 1
2.	C1 C2 C3 C4	Конденсатори ГОСТ 21415-15 КМ-9,1 нФ -16В КМ-4,3 нФ-16В КМ-9,1 нФ -16В КМ-4,3 нФ-16В	1 1 1 1

Використана література

1. Коваль Ю.О., Гринченко Л.В., Милютченко, О.І. Рибін. Основи теорії кіл. – Ч.1: Навч. підручник. – Харків: ТОВ «Компанія СМІТ», 2006. – 492 с.

2. Куликовский А.А. “Справочник по теоретическим основам радиоэлектроники”. – Том 2. – М.: Энергия, 1977.

3. Терещук Р.М. и др. “Полупроводниковые приёмно-усилительные устройства”. – Справ. Радиолюбителя. – К.: Наук. думка, 1988.

22