Потенциальная энергия упругой |
деформации (пружины) |
•Найдём работу, совершаемую при деформации упругой пружины.
Сила упругости |
где k – |
коэффициент упругости. |
|
•Сила непостоянна, поэтому элементарная работа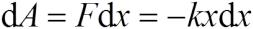 
(Знак минус говорит о том, что работа совершена над пружиной).
Тогда
т.е. A = U1 – U2. Примем: U2 = 0, U = U1, тогда
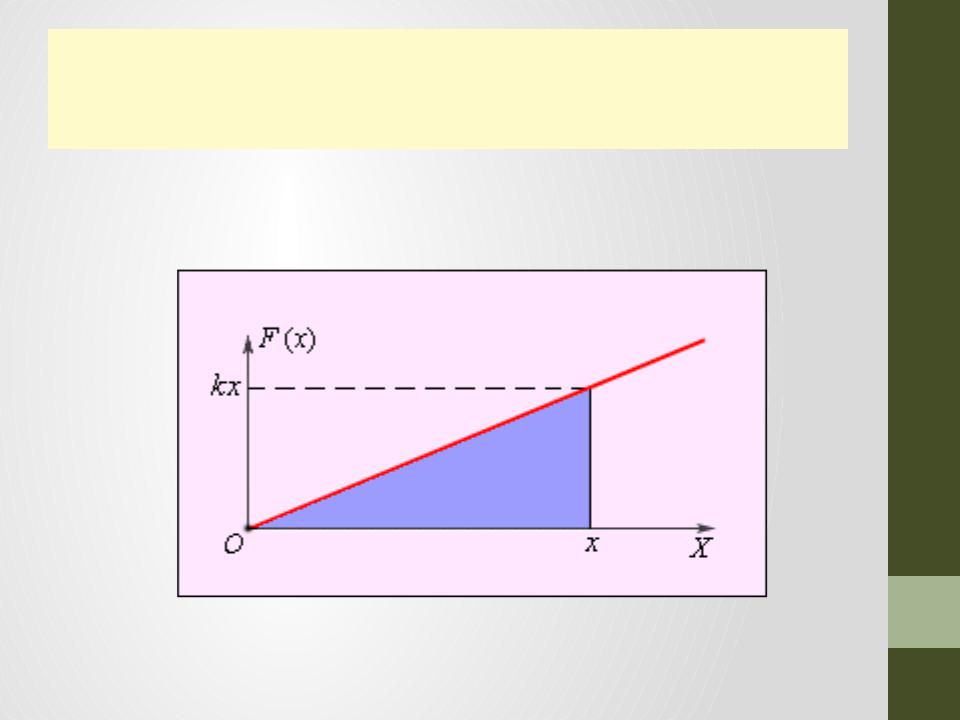
Потенциальная энергия упругой деформации (пружины)
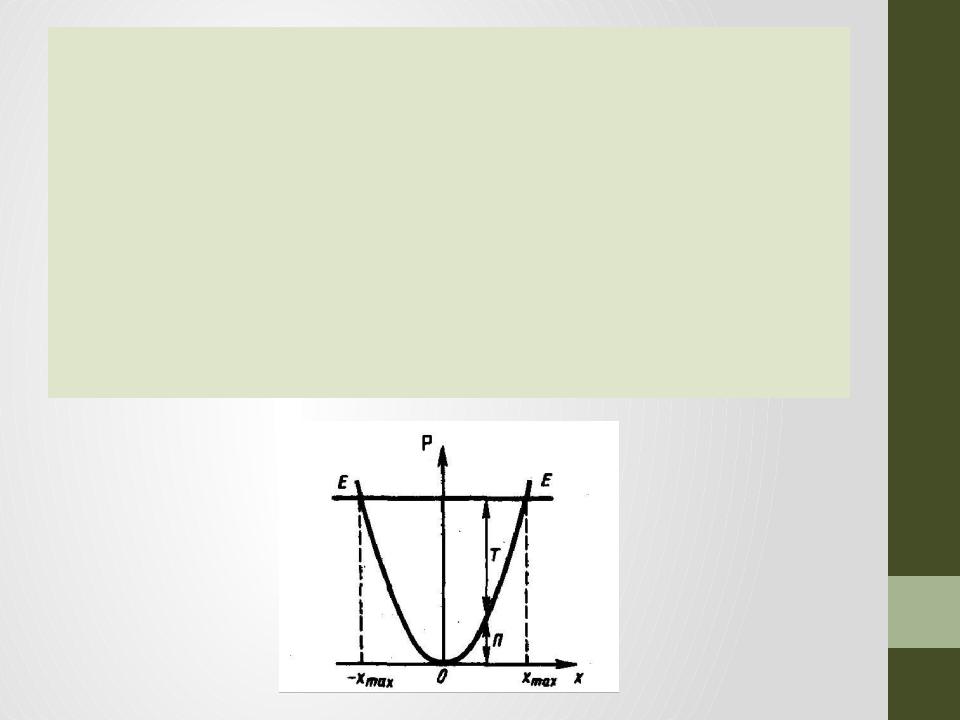
•Зависимость потенциальной энергии упругодеформированного тела U=кх2/2 от деформации х имеет вид параболы, где график заданной полной энергии тела Е - горизонтальная прямая (параллельная оси абсцисс х).
•С ростом деформации х потенциальная энергия тела растет, а кинетическая - уменьшается.
•Абсцисса xmax показывает максимально возможную деформацию растяжения тела, a -хmax - максимально возможную деформацию сжатия тела. Если х = ±хmax, то T=0 и U=E=kx2/2, в этом случае потенциальная энергия максимальна и равной полной энергии.
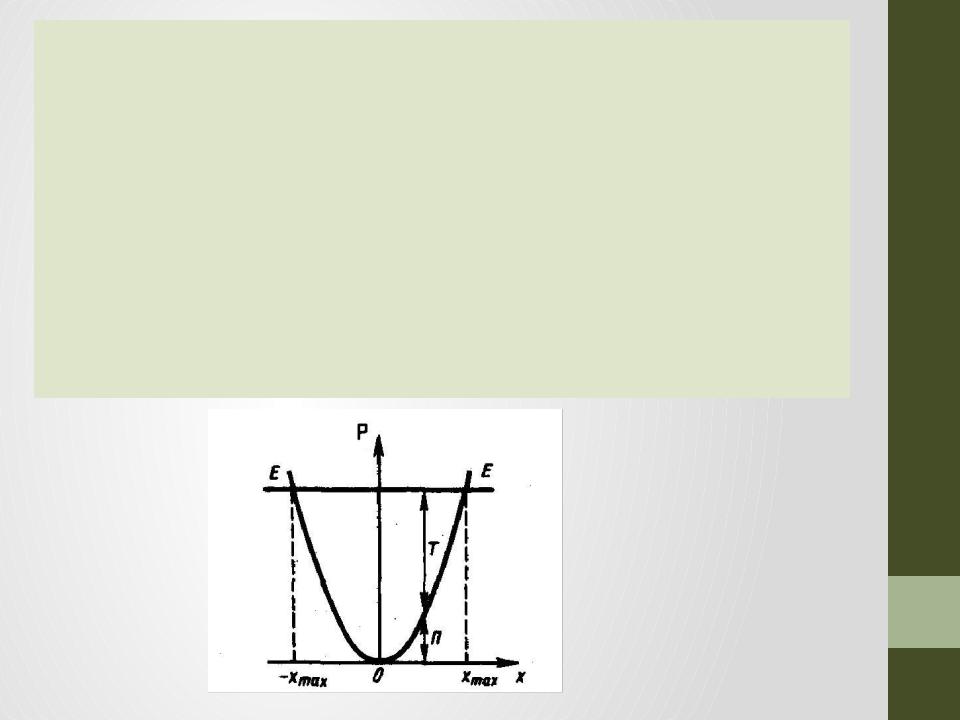
•Из графика на рис. вытекает, что если полная энергии тела равна Е, то тело не может сместиться правее хmax и левее -хmax, причем т.к. кинетическая энергия не может быть меньшей нуля и, следовательно, потенциальная энергия никогда не может быть больше полной энергии.
•В этом случае говорят, что тело находится в потенциальной яме с координатами -хmax≤x≤xmax.
Связь между потенциальной |
энергией и силой |
•Пространство, в котором действуют
консервативные силы, называется
потенциальным полем.
•Каждой точке потенциального поля
соответствует некоторое значение силы ,действующей на тело, и некоторое
значение потенциальной энергии U.
• Значит, между силой и U должна быть связь.
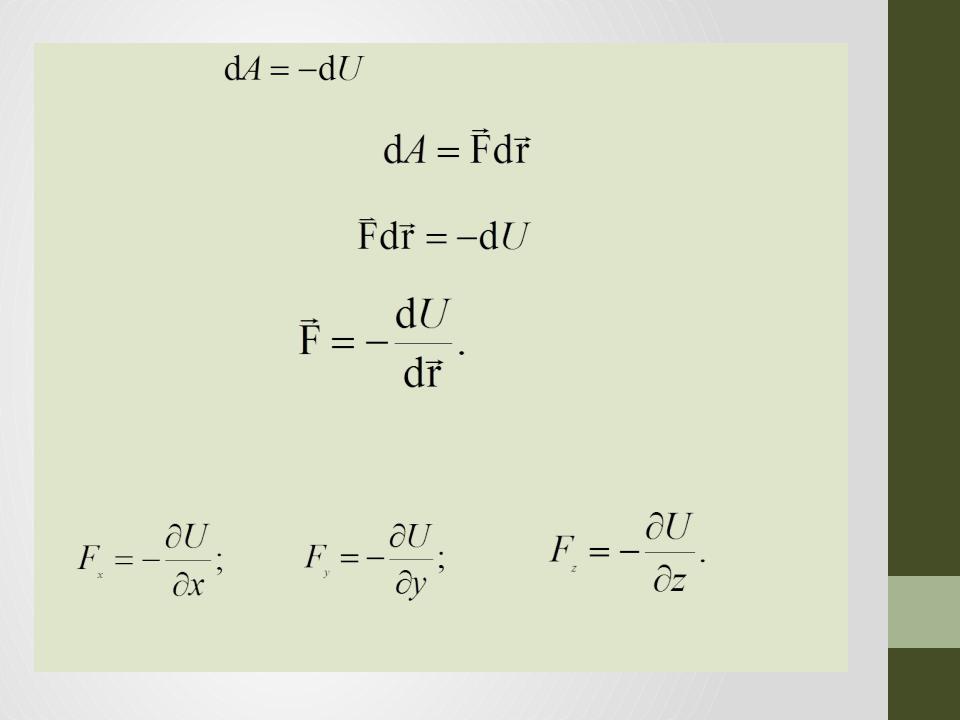
• Так как
• С другой стороны
• Следовательно
• Проекции вектора силы на оси координат:
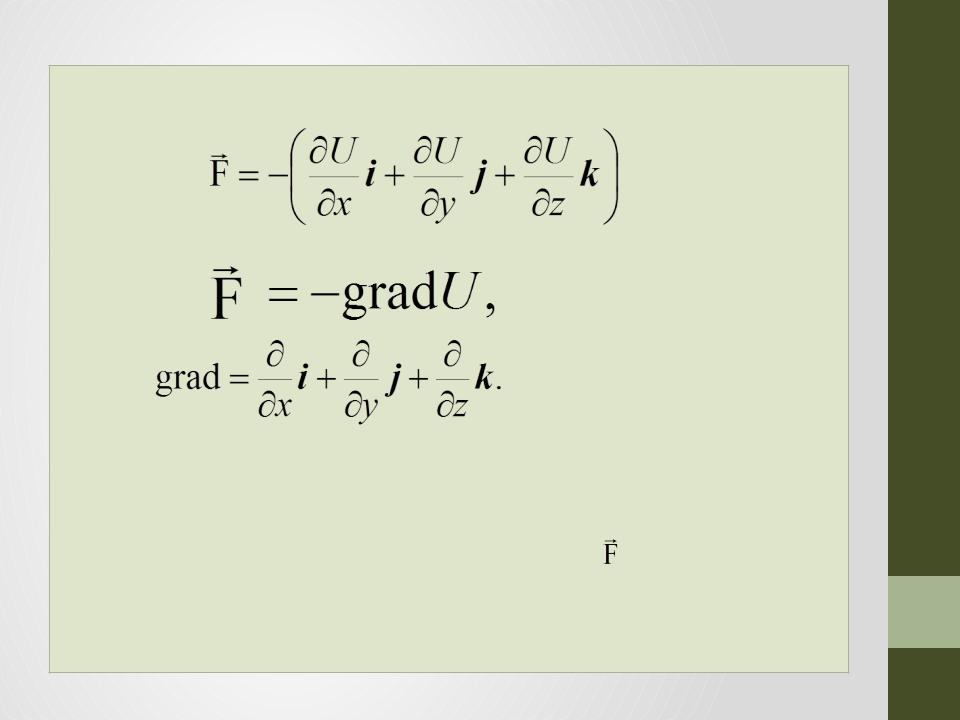
• Вектор силы можно записать через проекции: |
или |
где |
Градиент – это вектор, показывающий |
направление наибыстрейшего увеличения |
функции. |
Т.к. в формуле стоит знак «минус», то |
направлен в сторону наибыстрейшего |
уменьшения U. |
Закон сохранения механической энергии
•В сороковых годах девятнадцатого века трудами Р. Майера, Г. Гельмгольца и Дж. Джоуля (все в разное время и независимо друг от друга) был доказан закон сохранения и превращения энергии.
•Рассмотрим систему, состоящую из N-частиц.
•Силы взаимодействия между частицами –
консервативные.
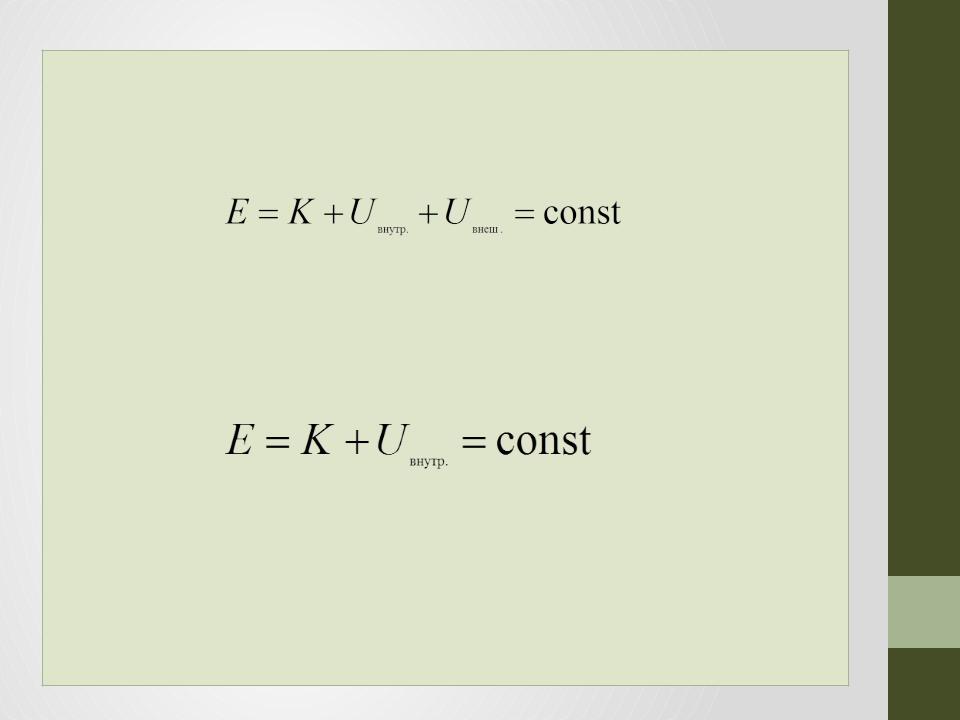
•Кроме внутренних сил, на частицы действуют внешние консервативные и неконсервативные силы, т.е. рассматриваемая система частиц или тел консервативна. Тогда для этой системы можно найти полную энергию системы
•Для механической энергии закон сохранения звучит так:
полная механическая энергия консервативной системы материальных точек остаётся постоянной. Для замкнутой системы, т.е. для системы, на которую не действуют внешние силы, можно записать:
•т.е. полная механическая энергия замкнутой системы материальных точек, между которыми действуют только консервативные силы, остаётся постоянной.
•Если в замкнутой системе действуют неконсервативные силы, то полная механическая энергия системы не сохраняется
– частично она переходит в другие виды энергии, неконсервативные.
•Система, в которой механическая энергия переходит в другие виды энергии, называется диссипативной, сам процесс перехода называется диссипацией энергии.
•
В диссипативной, изолированной от внешнего воздействия системе остаётся постоянной сумма всех видов энергии (механической, тепловой и т.д.) Здесь действует общий закон сохранения энергии.